一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.
(1)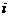 是虚数单位,复数
是虚数单位,复数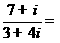 ( )
( )
(A)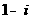 (B)
(B)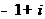 (C)
(C)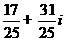 (D)
(D)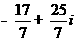
解: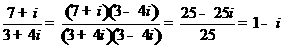 ,选A.
,选A.
(2)设变量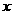 ,
,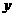 满足约束条件
满足约束条件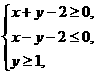 则目标函数
则目标函数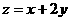 的最小值为( )
的最小值为( )
(A)2 (B)3 (C)4 (D)5
解:作出可行域,如图

结合图象可知,当目标函数通过点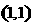 时,
时,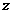 取得最小值3,选B.
取得最小值3,选B.
(3)已知命题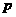 :
: ,总有
,总有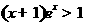 ,则
,则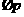 为( )
为( )
(A)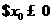 ,使得
,使得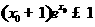 (B)
(B)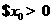 ,使得
,使得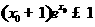
(C) ,总有
,总有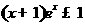 (D)
(D)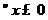 ,总有
,总有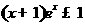
解:依题意知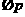 为:
为: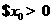 ,使得
,使得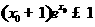 ,选B.
,选B.
(4)设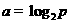 ,
,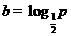 ,
,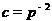 ,则( )
,则( )
(A)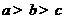 (B)
(B)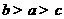 (C)
(C)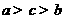 (D)
(D)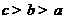
解:因为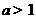 ,
,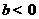 ,
,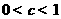 ,所以
,所以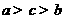 ,选C.
,选C.
(5)设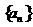 是首项为
是首项为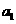 ,公差为
,公差为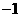 的等差数列,
的等差数列,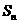 为其前
为其前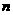 项和.若
项和.若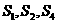 成等比数列,则
成等比数列,则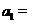 ( )
( )
(A)2 (B)-2 (C)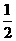 (D)
(D)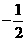
解:依题意得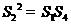 ,所以
,所以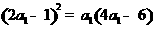 ,解得
,解得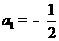 ,选D.
,选D.
(6)已知双曲线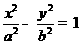
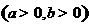 的一条渐近线平行于直线
的一条渐近线平行于直线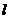 :
: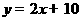 ,双曲线的一个焦点在直线
,双曲线的一个焦点在直线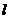 上,则双曲线的方程为( )
上,则双曲线的方程为( )
(A)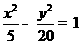 (B)
(B)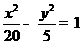
(C)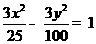 (D)
(D)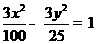
解:依题意得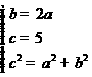 ,所以
,所以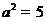 ,
,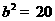 ,选A.
,选A.
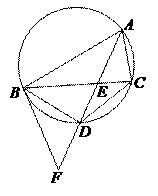
(7)如图,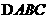 是圆的内接三角形,
是圆的内接三角形,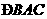 的平分线交圆于点
的平分线交圆于点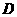 ,交
,交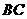 于点
于点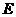 ,过点
,过点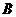 的圆的切线与
的圆的切线与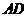 的延长线交于点
的延长线交于点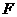 .在上述条件下,给出下列四个结论:①
.在上述条件下,给出下列四个结论:①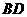 平分
平分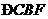 ;②
;②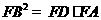 ;③
;③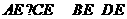 ;④
;④ .则所有正确结论的序号是( )
.则所有正确结论的序号是( )
(A)①② (B)③④ (C)①②③ (D)①②④
解:由弦切角定理得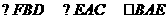 ,
,
又 ,
,
所以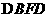 ∽
∽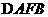 ,所以
,所以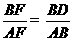 ,
,
即 ,排除A、C.
,排除A、C.
又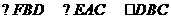 ,排除B,选D.
,排除B,选D.
(8)已知函数
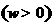 ,
,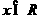 ,在曲线
,在曲线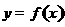 与直线
与直线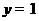 的交点中,若相邻交点距离的最小值为
的交点中,若相邻交点距离的最小值为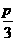 ,则
,则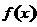 的最小正周期为( )
的最小正周期为( )
(A)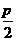 (B)
(B)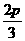 (C)
(C)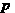 (D)
(D)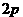
解:因为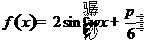 ,所以
,所以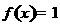 得
得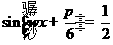 ,
,
所以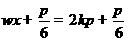 或
或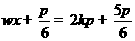 ,
,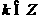 .
.
因为相邻交点距离的最小值为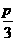 ,所以
,所以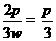 ,
,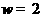 ,
,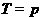 ,选C.
,选C.
第Ⅱ卷
二、填空题(本大题共6个小题,每小题5分,共30分.把答案填在题中横线上.)
(9)某大学为了解在校本科生对参加某项社会实践活动的意向,拟采用分层抽样的方法,从该校四个年级的本科生中抽取一个容量为300的样本进行调查.已知该校一年级、二年级、三年级、四年级的本科生人数之比为4:5:5:6,则应从一年级本科生中抽取_______名学生.
解:应从一年级抽取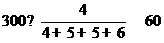 名.
名.
(10)已知一个几何体的三视图如图所示(单位:m),则该几何体的体积为_______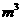 .
.
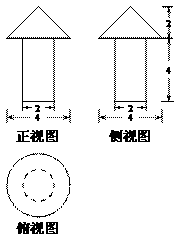
解:该几何体的体积为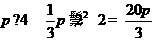
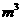 .
.
(11)阅读右边的框图,运行相应的程序,输出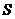 的值为________.
的值为________.
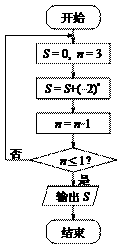
解: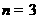 时,
时,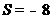 ;
;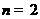 时,
时,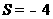 ,所以输出的
,所以输出的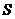 的值为-4.
的值为-4.
(12)函数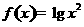 的单调递减区间值是________.
的单调递减区间值是________.
解:由复合函数的单调性知,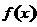 的单调递减区间是
的单调递减区间是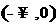 .
.
(13)已知菱形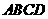 的边长为2,
的边长为2,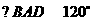 ,点
,点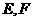 分别在边
分别在边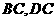 上,
上,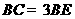 ,
,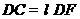 .若
.若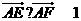 ,则
,则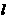 的值为_______.
的值为_______.
解:因为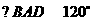 ,菱形的边长为2,所以
,菱形的边长为2,所以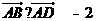 .
.
因为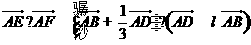 ,
,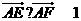 ,
,
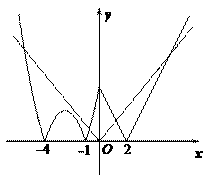
解得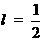 .
.
(14)已知函数
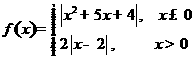 ,若函数
,若函数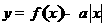 恰有4个零点,则实数
恰有4个零点,则实数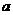 的取值范围为__________.
的取值范围为__________.
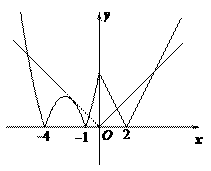
解:作出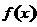 的图象,如图
的图象,如图
当直线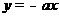 与函数
与函数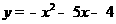 相切时,由
相切时,由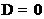 可得
可得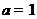 ,所以
,所以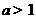 ;又当
;又当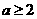 时,在
时,在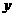 轴右侧只有一个交点,∴
轴右侧只有一个交点,∴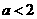 ,
,
所以,实数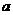 的取值范围为
的取值范围为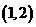 .
.
三、解答题(本题共6道大题,满分80分.解答应写出文字说明,证明过程或演算步骤.)
(15)(本小题满分13分)
某校夏令营有3名男同学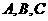 和3名女同学
和3名女同学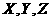 ,其年级情况如下表:
,其年级情况如下表:
| 一年级 | 二年级 | 三年级 |
男同学 |
|
|
|
女同学 |
|
|
|
现从这6名同学中随机选出2人参加知识竞赛(每人被选中的可能性相同).
(Ⅰ)用表中字母列举出所有可能的结果;
(Ⅱ)设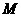 为事件“选出的2人来自不同年级且恰有1名男同学和1名女同学”,求事件
为事件“选出的2人来自不同年级且恰有1名男同学和1名女同学”,求事件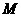 发表的概率.
发表的概率.
解:(Ⅰ)所有可能的结果共有15种:
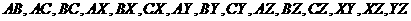 .
.
(Ⅱ)符合条件的有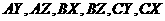 ,
,
∴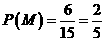 .
.
(16)(本小题满分13分)
在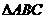 中,内角
中,内角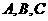 的对边分别为
的对边分别为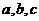 .已知
.已知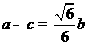 ,
,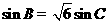 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)求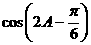 的值.
的值.
解:(Ⅰ)∵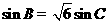 ,∴
,∴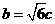 ,
,
代入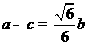 ,解得
,解得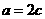 ,
,
由余弦定理得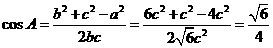 .
.
(Ⅱ)由(Ⅰ)得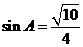 ,
,
∴ ,
,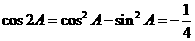 ,
,
∴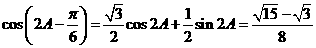 .
.
(17)(本小题满分13分)
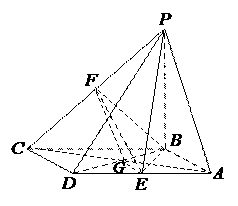
如图,四棱锥 的底面是平行四边形,
的底面是平行四边形,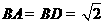 ,
,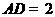 ,
,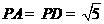 ,
,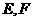 分别是棱
分别是棱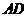 ,
,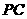 的中点.
的中点.
(Ⅰ)证明 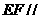 平面
平面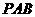 ;
;
(Ⅱ)若二面角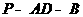 为
为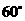 ,
,
(ⅰ)证明 平面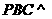 平面
平面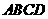 ;
;
(ⅱ)求直线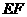 与平面
与平面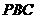 所成角的正弦值.
所成角的正弦值.
(解法一)(Ⅰ)证明:连结 ,
,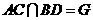 ,则
,则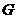 是
是
 、
、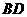 的中点, 连结
的中点, 连结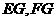 ,
,
则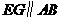 ,
,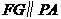 ,
,
∴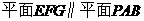 ,又
,又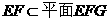 ,
,
故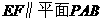 .
.
(Ⅱ)(ⅰ)∵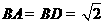 ,
,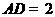 ,∴
,∴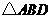 是等腰直角三角形.
是等腰直角三角形.
取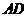 的中点
的中点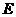 ,则
,则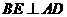 ,
,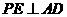 ,∴
,∴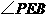 是二面角
是二面角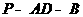 的平面角,即
的平面角,即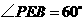
又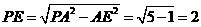 ,且
,且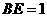 ,
,
由余弦定理得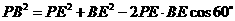
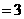 ,∴
,∴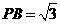 .
.
∵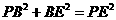 ,∴
,∴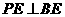 ,又
,又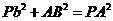 ,∴
,∴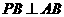 ,
,
∴ ,又
,又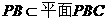 ,∴平面
,∴平面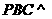 平面
平面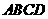 .
.
(ⅱ)∵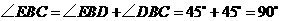 ,∴
,∴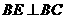 ,
,
由(ⅰ)知平面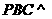 平面
平面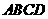 ,∴
,∴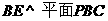 ,
,
所以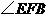 是
是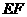 与
与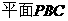 所成的角.
所成的角.
在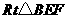 中,
中,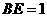 ,
,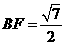 ,∴
,∴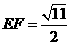 ,
,
∴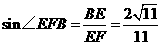 ,即直线
,即直线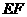 与平面
与平面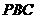 所成角的正弦值是
所成角的正弦值是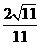 .
.
(解法二)(Ⅰ)、证明:取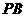 的中点
的中点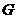 ,连结
,连结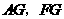 ,
,
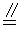
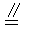
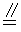 ∵
∵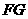
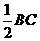 ,
,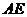
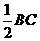 ,∴
,∴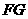
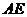 ,
,
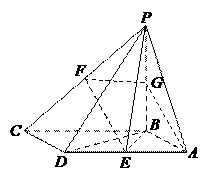 所以四边形
所以四边形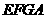 是平行四边形,∴
是平行四边形,∴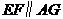 ,
,
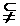 又
又
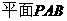 ,∴
,∴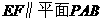 .
.
(Ⅱ)同解法一.
(18)(本小题满分13分)
设椭圆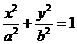 (
(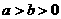 )的左、右焦点为
)的左、右焦点为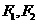 ,右顶点为
,右顶点为 ,上顶点为
,上顶点为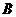 .已知
.已知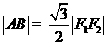 .
.
(Ⅰ)求椭圆的离心率;
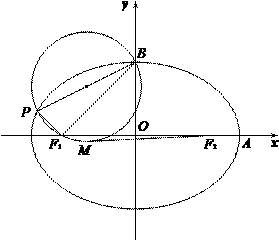
(Ⅱ)设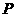 为椭圆上异于其顶点的一点,以线段
为椭圆上异于其顶点的一点,以线段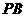 为直径的圆经过点
为直径的圆经过点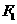 ,经过点
,经过点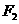 的直线
的直线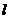 与该圆相切于点
与该圆相切于点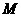 ,
,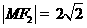 ,求椭圆的方程.
,求椭圆的方程.
(Ⅰ)解:依题意得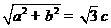 ,∴
,∴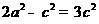 ,解得
,解得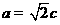 ,
,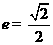 .1
.1
(Ⅱ)解:由(Ⅰ)知椭圆方程可化为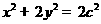 .
.
因为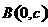 ,所以直线
,所以直线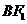 的斜率
的斜率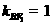 .
.
因为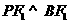 ,所以直线
,所以直线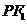 的斜率
的斜率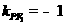 ,
,
直线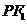 的方程为
的方程为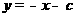 .
.
设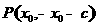 ,则有
,则有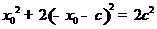 ,解得
,解得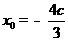 或
或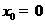 (舍),所以
(舍),所以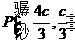 .
.
因为线段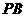 的中点为
的中点为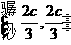 ,所以圆的方程为
,所以圆的方程为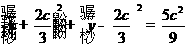 .
.
因为直线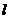 与该圆相切,且
与该圆相切,且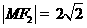 ,所以
,所以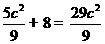 ,解得
,解得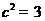 .
.
所以椭圆方程为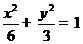 .
.
(19)(本小题满分14分)
已知函数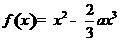
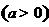 ,
,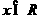 .
.
(Ⅰ)求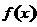 的单调区间和极值;
的单调区间和极值;
(Ⅱ)若对于任意的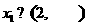 ,都存在
,都存在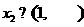 ,使得
,使得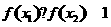 .求
.求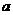 的取值范围.
的取值范围.
(Ⅰ)解:因为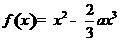 ,所以
,所以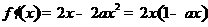 .
.
令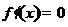 得
得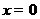 或
或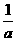 .
.
因为当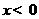 或
或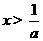 时,
时,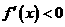 ,
,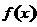 单调递减,当
单调递减,当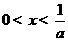 时,
时,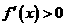 ,
,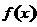 单调递增,
单调递增,
所以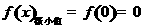 ,
,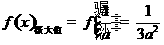 .
.
(Ⅱ)解:由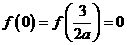 及(Ⅰ)知,当
及(Ⅰ)知,当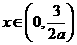 时,
时,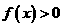 ;当
;当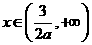 时,
时,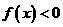 .
.
设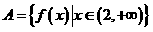 ,
,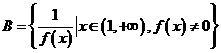 ,则“对于任意的
,则“对于任意的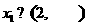 ,都存在
,都存在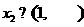 ,使得
,使得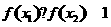 ”等价于
”等价于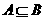 .显然
.显然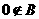 .下面分三种情况讨论
.下面分三种情况讨论
⑴当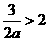 ,即
,即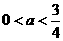 时,由
时,由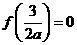 可知,
可知, ,但
,但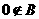 ,∴
,∴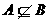 .
.
⑵当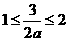 ,即
,即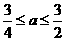 时,
时,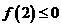 ,且此时
,且此时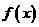 在
在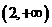 单调递减,故
单调递减,故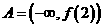 ,因此
,因此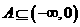 ;由
;由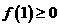 知
知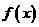 在
在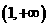 上的取值范围包含
上的取值范围包含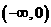 ,则
,则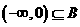 .所以此时满足
.所以此时满足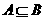 .
.
⑶当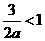 ,即
,即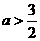 时,因为
时,因为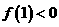 ,且
,且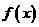 在
在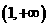 上单调递减,所以
上单调递减,所以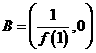 ;又
;又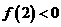 ,
,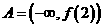 ,所以
,所以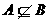 .
.
综上,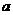 的取值范围是
的取值范围是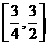 .
.
(20)(本小题满分14分)
已知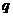 和
和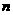 均为给定的大于1的自然数.设集合
均为给定的大于1的自然数.设集合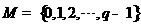 ,集合
,集合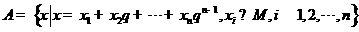 .
.
(Ⅰ)当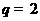 ,
,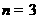 时,用列举法表示集合
时,用列举法表示集合 ;
;
(Ⅱ)设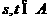 ,
,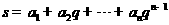 ,
,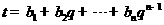 ,其中
,其中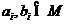 ,
,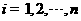 . 证明:若
. 证明:若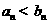 ,则
,则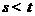 .
.
(Ⅰ)解:当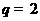 ,
,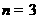 时,
时,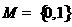 ,
,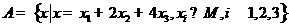 ,
,
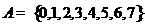 .
.
(Ⅱ)证明:因为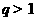 ,所以
,所以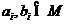 ,所以
,所以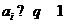 ,
,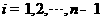 ,
,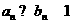 .
.
所以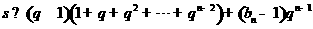
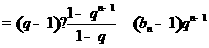
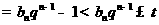 .
.
所以,若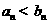 ,则
,则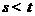 .
.