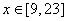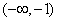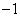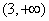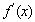一.选择题
(1)D (2)C (3)C (4)A (5)B (6)B
(7)A (8)C (9)D (10)B (11)A (12)C
二.填空题
(13) 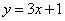 (14)
(14)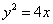 (15)
(15)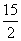 (16)0
(16)0
三.解答题
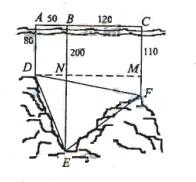
(17) 解:
作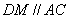 交BE于N,交CF于M.
交BE于N,交CF于M.
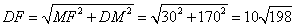 ,
,

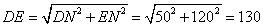
 ,
,
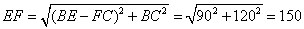 . ......6分
. ......6分

在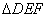 中,由余弦定理,
中,由余弦定理,
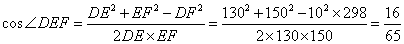 . ......12分
. ......12分
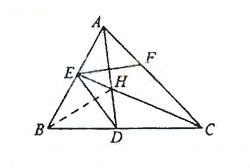
(18)解:
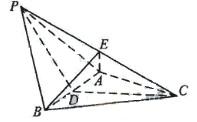
(Ⅰ)因为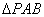 是等边三角形,
是等边三角形,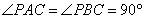 ,
,
所以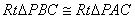 ,可得
,可得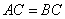 。
。
如图,取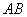 中点
中点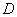 ,连结
,连结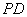 ,
,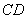 ,
,
则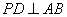 ,
,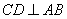 ,
,
所以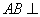 平面
平面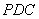 ,
,
所以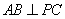 。 ......6分
。 ......6分

(Ⅱ)作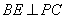 ,垂足为
,垂足为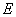 ,连结
,连结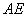 .
.
因为
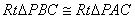 ,
,
所以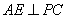 ,
,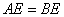 .
.
由已知,平面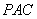
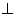 平面
平面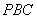 ,故
,故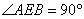 . ......8分
. ......8分
因为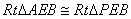 ,所以
,所以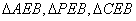 都是等腰直角三角形。
都是等腰直角三角形。
由已知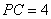 ,得
,得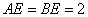 ,
, 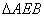 的面积
的面积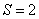 .
.
因为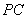
 平面
平面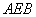 ,
,
所以三角锥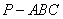 的体积
的体积
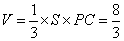 .......12分
.......12分
(19)解:
(Ⅰ)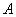 类工人中和
类工人中和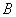 类工人中分别抽查25名和75名。 ......4分
类工人中分别抽查25名和75名。 ......4分
(Ⅱ)(ⅰ)由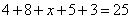 ,得
,得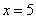 ,
,
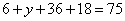 ,得
,得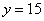 。
。

频率分布直方图如下
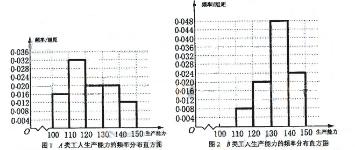 ......8分
......8分
从直方图可以判断: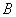 类工人中个体间的差异程度更小。 ......9分
类工人中个体间的差异程度更小。 ......9分
(ii) 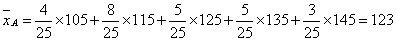 ,
,
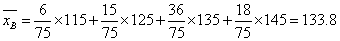 ,
,

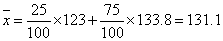
A类工人生产能力的平均数,B类工人生产能力的平均数以及全厂工人生产能力的平均数的估计值分别为123,133.8和131.1.
(20)解:
(Ⅰ)设椭圆长半轴长及分别为a,c,由已知得

{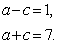 解得a=4,c=3,
解得a=4,c=3,
所以椭圆C的方程为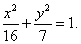


(Ⅱ)设M(x,y),P(x,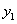 ),其中
),其中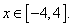 由已知得
由已知得
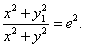
而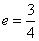 ,故
,故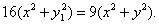 ①
①
由点P在椭圆C上得 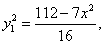


代入①式并化简得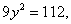
所以点M的轨迹方程为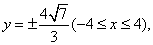 轨迹是两条平行于x轴的线段.
轨迹是两条平行于x轴的线段.

(21)解:
(Ⅰ)当a=1时,对函数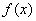 求导数,得
求导数,得
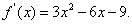
令 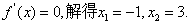


列表讨论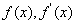 的变化情况:
的变化情况:
|
|
| (-1,3) | 3 |
|
| + | 0 | — | 0 | + |
|
| 极大值6 |
| 极小值-26 |
|
所以,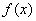 的极大值是
的极大值是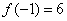 ,极小值是
,极小值是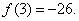
(Ⅱ)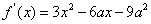 的图像是一条开口向上的抛物线,关于x=a对称.
的图像是一条开口向上的抛物线,关于x=a对称.
若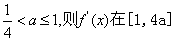 上是增函数,从而
上是增函数,从而

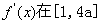 上的最小值是
上的最小值是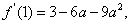 最大值是
最大值是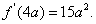
由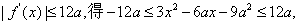 于是有
于是有

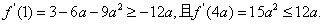
由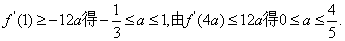
所以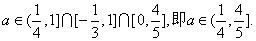


若a>1,则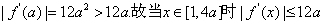 不恒成立.
不恒成立.
所以使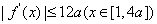 恒成立的a的取值范围是
恒成立的a的取值范围是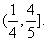


(22)解:
(Ⅰ)在△ABC中,因为∠B=60°,

所以∠BAC+∠BCA-=120°.
因为AD,CE是角平分线,
所以∠HAC+∠HCA=60°,

故∠AHC=120°.
于是∠EHD=∠AHC=120°.
因为∠EBD+∠EHD=180°,
所以B,D,H,E四点共圆。
(Ⅱ)连结BH,则BH为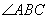 的平分线,得
的平分线,得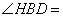 30°
30°

由(Ⅰ)知B,D,H,E四点共圆,

所以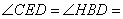 30°
30°
又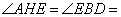 60°,由已知可得
60°,由已知可得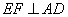 ,
,
可得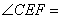 30°
30°

所以CE平分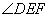
(23)解:
(Ⅰ)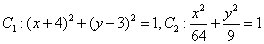


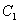 为圆心是
为圆心是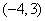 ,半径是1的圆。
,半径是1的圆。
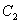 为中心是坐标原点,焦点在
为中心是坐标原点,焦点在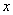 轴上,长半轴长是8,短半轴长是3的椭圆。
轴上,长半轴长是8,短半轴长是3的椭圆。

(Ⅱ)当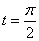 时,
时,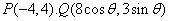 ,故
,故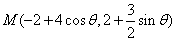
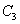 为直线
为直线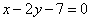 ,
,
M到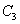 的距离
的距离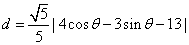


从而当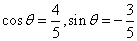 时,
时,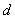 取得最小值
取得最小值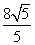


(24)解:
(Ⅰ)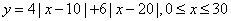


(Ⅱ)依题意,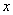 满足
满足
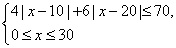
解不等式组,其解集为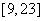
所以