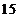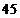三.解答题
17.(本小题满分12分)已知等差数列 的公差
的公差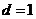 ,前
,前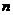 项和为
项和为 .
.
(1)若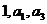 成等比数列,求
成等比数列,求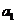 ;
;
(2)若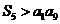 ,求
,求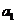 的取值范围.
的取值范围.
本小题主要考查等比等差数列、等比数列和不等式等基础知识,考查运算求解能力,考查函数与方程思想、化归与转化思想.满分12分.
解:(1)因为数列 的公差
的公差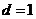 ,且
,且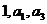 成等比数列,
成等比数列,
所以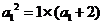 ,
,
即 ,解得
,解得 或
或 .
.
(2)因为数列 的公差
的公差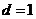 ,且
,且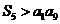 ,
,
所以 ;
;
即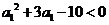 ,解得
,解得
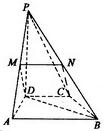
18.(本小题满分12分)如图,在四棱锥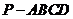 中,
中,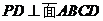 ,
, ,
, ,
, ,
, ,
,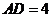 ,
, .
.
(1)当正视图方向与向量 的方向相同时,画出四棱锥
的方向相同时,画出四棱锥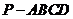 的正视图.(要求标出尺寸,并画出演算过程);
的正视图.(要求标出尺寸,并画出演算过程);
(2)若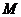 为
为 的中点,求证:
的中点,求证: ;
;
(3)求三棱锥 的体积.
的体积.

本小题主要考查直线与直线、直线与平面的位置关系及几何体的三视图和体积等基础知识,考查空间想象能力,推理论证能力.运算求解能力,考查数形结合能力、化归与转化思想,满分12分.
解法一:
(Ⅰ)在梯形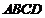 中,过点
中,过点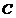 作
作 ,垂足为
,垂足为 ,
,
由已知得,四边形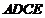 为矩形,
为矩形,
在 中,由
中,由 ,
, ,依勾股定理得:
,依勾股定理得:
 ,从而
,从而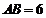
又由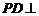 平面
平面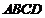 得,
得,
 从而在
从而在 中,由
中,由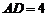 ,
, ,得
,得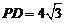
正视图如右图所示:
(Ⅱ)取 中点
中点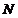 ,连结
,连结 ,
,
在 中,
中, 是
是 中点,
中点,
∴ ,
, ,又
,又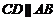 ,
,
∴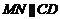 ,
,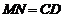
∴四边形 为平行四边形,∴
为平行四边形,∴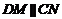
又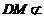 平面
平面 ,
, 平面
平面
∴ 平面
平面
(Ⅲ)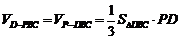
又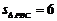 ,
,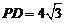 ,所以
,所以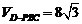
解法二:
(Ⅰ)同解法一

(Ⅱ)取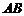 的中点
的中点 ,连结
,连结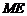 ,
,
在梯形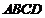 中,
中, ,且
,且
∴四边形 为平行四边形
为平行四边形
∴ ,又
,又 平面
平面 ,
, 平面
平面
∴ 平面
平面 ,又在
,又在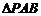 中,
中,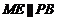
 平面
平面 ,
, 平面
平面
∴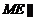 平面
平面 .又
.又 ,
,
∴平面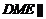 平面
平面 ,又
,又 平面
平面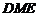
∴ 平面
平面
(Ⅲ)同解法一
19.(本小题满分12分)某工厂有25周岁以上(含25周岁)工人300名,25周岁以下工人200名.为研究工人的日平均生产量是否与年龄有关.现采用分层抽样的方法,从中抽取了100名工人,先统计了他们某月的日平均生产件数,然后按工人年龄在“25周岁以上(含25周岁)”和“25周岁以下”分为两组,在将两组工人的日平均生产件数分成5组: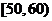 ,
, ,
, ,
, ,
, 分别加以统计,得到如图所示的频率分布直方图.
分别加以统计,得到如图所示的频率分布直方图.
(1)从样本中日平均生产件数不足60件的工人中随机抽取2人,求至少抽到一名“25周岁以下组”工人的频率.
(2)规定日平均生产件数不少于80件者为“生产能手”,请你根据已知条件完成 的列联表,并判断是否有
的列联表,并判断是否有
的把握认为“生产能手与工人所在的年龄组有关”?


附表:

本小题主要考查古典概型、抽样方法、独立性检验等基础知识,考查运算求解能力、应用意识,考查必然和或然思想、化归与转化思想等,满分12分.
解:(Ⅰ)由已知得,样本中有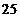 周岁以上组工人
周岁以上组工人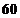 名,
名,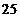 周岁以下组工人
周岁以下组工人 名
名
所以,样本中日平均生产件数不足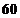 件的工人中,
件的工人中,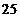 周岁以上组工人有
周岁以上组工人有 (人),
(人),
记为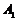 ,
,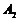 ,
, ;
;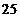 周岁以下组工人有
周岁以下组工人有 (人),记为
(人),记为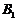 ,
,
从中随机抽取 名工人,所有可能的结果共有
名工人,所有可能的结果共有 种,他们是:
种,他们是: ,
, ,
,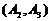 ,
, ,
, ,
, ,
, ,
, ,
, ,
,
其中,至少有名“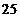 周岁以下组”工人的可能结果共有
周岁以下组”工人的可能结果共有 种,它们是:
种,它们是: ,
, ,
, ,
, ,
, ,
, ,
, .故所求的概率:
.故所求的概率: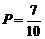
(Ⅱ)由频率分布直方图可知,在抽取的 名工人中,“
名工人中,“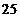 周岁以上组”中的生产能手
周岁以上组”中的生产能手 (人),“
(人),“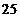 周岁以下组”中的生产能手
周岁以下组”中的生产能手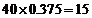 (人),据此可得
(人),据此可得 列联表如下:
列联表如下:
生产能手 | 非生产能手 | 合计 | |
|
|
|
|
|
|
|
|
合计 |
|
|
|
所以得: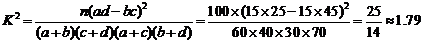
因为 ,所以没有
,所以没有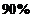 的把握认为“生产能手与工人所在的年龄组有关”
的把握认为“生产能手与工人所在的年龄组有关”