(1)复数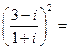
(A)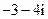 (B)
(B)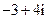 (C)
(C)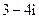 (D)
(D)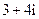
【答案】A
【命题意图】本试题主要考查复数的运算.
【解析】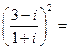
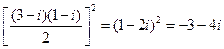 .
.
(2).函数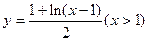 的反函数是
的反函数是
(A) 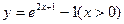 (B)
(B)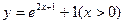
(C)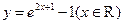 (D)
(D)

(3).若变量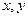 满足约束条件
满足约束条件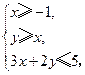 则
则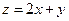 的最大值为
的最大值为
(A)1 (B)2 (C)3 (D)4
【答案】C
【命题意图】本试题主要考查简单的线性规划问题.
【解析】可行域是由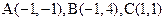 构成的三角形,可知目标函数过C时最大,最大值为3,故选C.
构成的三角形,可知目标函数过C时最大,最大值为3,故选C.
(4).如果等差数列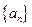 中,
中,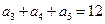 ,那么
,那么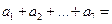
(A)14 (B)21 (C)28 (D)35【答案】C
【命题意图】本试题主要考查等差数列的基本公式和性质.
【解析】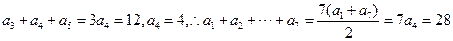
(5)不等式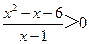 的解集为
的解集为
(A)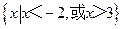 (B)
(B)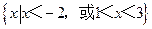
(C) 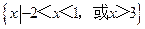 (D)
(D)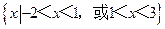

(6)将标号为1,2,3,4,5,6的6张卡片放入3个不同的信封中.若每个信封放2张,其中标号为1, 2的卡片放入同一信封,则不同的方法共有
2的卡片放入同一信封,则不同的方法共有
(A)12种 (B)18种 (C)36种 (D)54种

(7)为了得到函数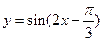 的图像,只需把函数
的图像,只需把函数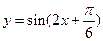 的图像
的图像
(A)向左平移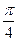 个长度单位 (B)向右平移
个长度单位 (B)向右平移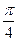 个长度单位
个长度单位

(C)向左平移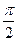 个长度单位 (D)向右平移
个长度单位 (D)向右平移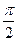 个长度单位
个长度单位
【答案】B
【命题意图】本试题主要考查三角函数图像的平移.
【解析】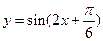 =
=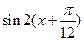 ,
,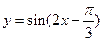 =
=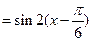 ,所以将
,所以将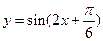 的图像向右平移
的图像向右平移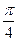 个长度单位得到
个长度单位得到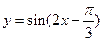 的图像,故选B.
的图像,故选B.
(8)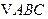 中,点
中,点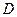 在
在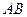 上,
上,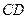 平方
平方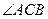 .若
.若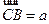
 ,
,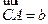 ,
,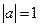 ,
,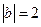 ,则
,则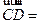
(A)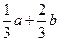 (B)
(B)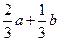 (C)
(C)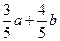 (D
(D )
)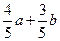
【答案】B
【命题意图】本试题主要考查向量的基本运算,考查角平分线定理.
【解析】因为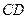 平分
平分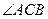 ,由角平分线定理得
,由角平分线定理得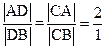 ,所以D为AB的三等分点,
,所以D为AB的三等分点, 且
且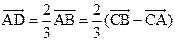 ,所以
,所以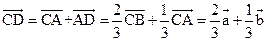 ,故选B.
,故选B.
(9) 已知正四棱锥
已知正四棱锥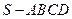 中,
中,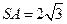 ,那么当该棱锥的体积最大时,它的高为
,那么当该棱锥的体积最大时,它的高为
(A)1 (B)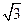 (C)2 (D)3
(C)2 (D)3

(10)若曲线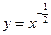 在点
在点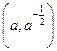 处的切线与两个坐标围成的三角形的面积为18,则
处的切线与两个坐标围成的三角形的面积为18,则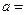
(A)64 (B)32 (C)16  (D)8
(D)8
【答案】A
【命题意图】本试题主要考查求导法则、导数的几何意义、切线的求法和三角形的面积公式,考查考生的计算能力..
【解析】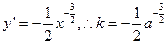 ,切线方程是
,切线方程是
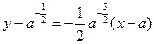 ,令
,令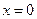 ,
,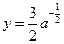 ,令
,令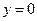 ,
,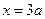 ,∴三角形的面积是
,∴三角形的面积是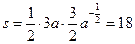 ,解得
,解得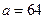 .故选A.
.故选A.
(11)与正方体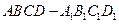 的三条棱
的三条棱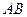 、
、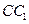 、
、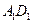 所在直线的距离相等的点
所在直线的距离相等的点
(A)有且只有1个 (B)有且只有2个
(C)有且只有3个 (D)有无数个

(12)已知椭圆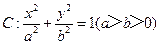 的离心率为
的离心率为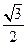 ,过右焦点
,过右焦点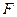 且斜率为
且斜率为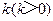

 的直线与
的直线与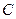 相交于
相交于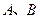 两点.若
两点.若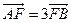 ,则
,则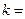
(A)1 (B)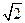 (C)
(C)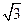 (D)2
(D)2













