I hate math, but there’s this statistics problem that has me geeking out.
我讨厌数学,但我还是被一个统计问题缠上了
It’s a question that seems really really simple but it’s stumped me.
这个问题看上去无比简单,但它还是难倒我了
And not just me, it has stumped thousands of people around the world,
而且,被难倒的除了我,还有成千上万人
including math professors and leading statisticians.
甚至包括很多数学教授以及顶尖的统计学者
But before we dive in, I’m going to introduce you to Zachery Crockett.
但是,在具体描述之前,我先给大家介绍一下扎切里·克罗基特
He first introduced me to the puzzle and I called him up to talk about it.
这道题就是他给我出的,我还跟他打电话讨论过
My name is Zachery Crockett, I’m a writer for Priceonomics.
我是扎切里·克罗基特,Priceonomics网站的编辑
Zachery and his girlfriend were confused by the problem too.
扎切里和他女朋友也都被这个问题难倒了
We just sat there debating the answer to this problem for two hours
我们就坐着讨论这个问题讨论了两个小时
and I don’t think any of us really understood it.
还是觉得我俩都没有真正理解这个问题
The puzzle we were all stumped by is called the Monty Hall Problem --
这个让我们都栽了跟头的难题就是所谓的“蒙提霍尔问题”(Monty Hall Problem)
named after the host of the game show that made it famous.
这一问题当初就是从蒙提·霍尔主持的游戏节目火气来的
the problem goes like this: there’s a brand new car behind one of three doors.
问题是这样的,这三道门有一扇后面有一台崭新的车
Behind the other 2 are goats.
另外两扇后面是山羊
Say you pick door 1.
假如你选了一号门
Monty then shows you the goat behind one of the doors you DIDN’T choose, say, door 3.
蒙提就会开启剩下两扇中有山羊的那一扇门,假定是三号门
Now here’s the question: You’re allowed to change your answer to Door 2.
那么现在问题来了:你可以改选二号门
Do you switch? Or stick with your original choice?
那你是改呢?还是坚持你原来的选择呢?
So yeah, I got interested in the Monty Hall Problem, did a little research,
没错,这个问题吸引了我,所以我就做了一项小小的研究
and then I found out there was this whole second angle to the story.
结果发现,这个问题还有一个全新的角度
You’ve never met a man that feared you a little bit because he thought you were much brighter than he was?
你就有遇到过会因为你比他更聪明而怕你的男性吗?
That’s Marilyn Vos Savant in 1988 being interviewed by Joe Franklyn.
这是玛丽莲·沃斯·莎凡特1988年接受乔·富兰克林采访的片段
Well, yeah, maybe I’ve met a man or two, maybe a couple a hundred like that.
嗯……遇到过,可能遇到过一两个,也可能遇到过很多
Marilyn is very intelligent.
玛丽莲非常聪明
In fact, back when the Guinness World Records actually kept track of this
实际上,当吉尼斯世界纪录还在关注这个问题的时候
she was the world’s highest IQ.
玛丽莲就是当时世界上智商最高的人
She now writes for Parade Magazine and has for the last 20 years.
她过去二十年到现在一直是《展示杂志》的签约作家
So the premise of the column was of course, like,
当然了,这个栏目的卖点就是:
here is the person with the world's highest IQ here to answer your challenging math questions.
他们有世界上智商最高的人来帮忙解答读者的数学难题
This brings us to September 1990, when a reader submitted to Marilyn...the Monty Hall Problem.
这一卖点把我们带到了1990年9月,一位读者给玛丽莲寄来了……蒙提霍尔问题
Is it to your advantage to switch your choice of doors?
改变选项会对参赛者更有利吗?
Now, if you’re like me the obvious answer is no.
如果你跟我一样,那么答案显然是“不会”
There are two doors so the chance of getting a car and not a goat is 50/50.
还剩下两扇门,所以选到车不选到羊的概率是50%
Bing.Bang.Boom.
小菜一碟嘛
But that’s the wrong answer, and Marilyn knew that.
但是,这个答案是错的,玛丽莲很清楚
She replied: “Yes; you should switch.” And here’s why.
她的回答是:“会,所以你应该改变主意”,理由是这样
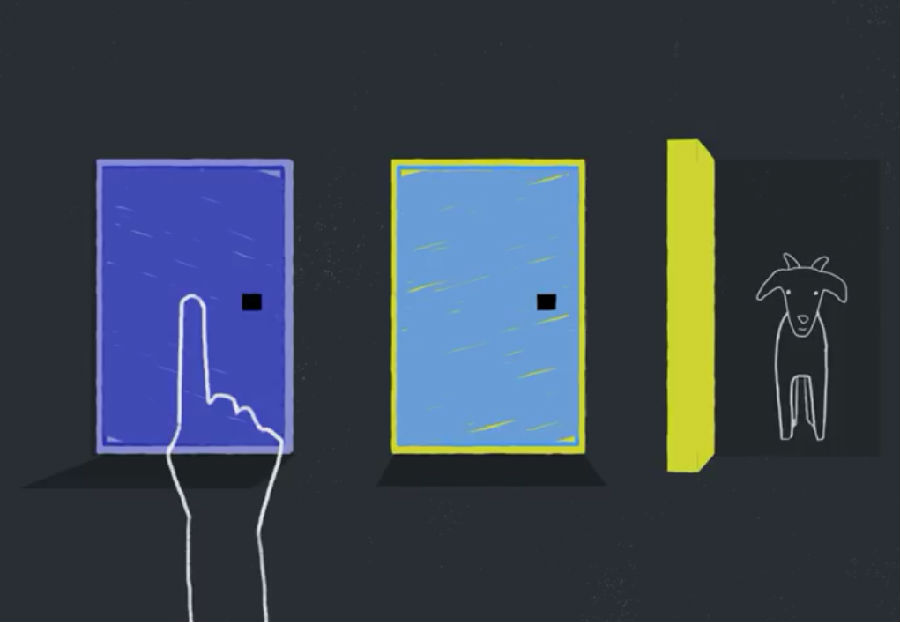
Here are 3 doors. There’s a goat behind 2 and a car behind 1.
这是三扇门,两扇门后都是羊,剩下一扇后面是汽车
In a blind test, you’re more likely to pick a goat than a car. In fact, you’re 2/3RDS likely.
盲选的话,你选到山羊的概率更大,具体概率是2/3
so let’s use that as our main scenario.
我们且把这一点当成故事的主线
You pick door 1.
假如你选一号门
So now, Monty Hall, who knows what’s behind all the doors,
那么现在,知道每扇门情况的蒙提·霍尔
is forced to reveal a goat regardless of the door you pick.
就不得不展示另一扇门的山羊
Since, in the most probable scenario, you’ve also picked a goat,
我们拿最可能的情况,也就是你选到了山羊的情况来看
the only door left is the one with the car.
剩下的一扇门后就是汽车了
So, now Monty Hall asks, “Would you rather keep the door you’ve picked, or switch?”
现在蒙提·霍尔问你了,“你是坚持原来的选择还是改变主意?”
Well, you should most definitely switch.
那么……你一定要改主意
If you do, you get the car 2/3rds of the time.
因为你真的改变主意的话,得到汽车的概率是2/3
Turns out when Marilyn correctly answered the Monty Hall Problem,
最后,当玛丽莲正确回答了蒙提·霍尔问题之后
she received thousands of letters from across the world, telling her she was flat out wrong.
她收到了来自世界各地的无数封信,都说她完全搞错了
I think part of her was a little bit surprised that she received 10,000 letters calling her an idiot.
我觉得,收到那么多骂她笨蛋的信,她可能还是会有一点惊讶吧
There was, without a doubt, a little bit of sexism at play here.
毫无疑问,这里面可能有性别歧视存在
Not only was her answer right, it wasn’t anything new.
玛丽莲的答案不仅仅是正确的,而且也不是什么新鲜事
The first time the Monty Hall problem was really conceived was in 1975.
蒙提·霍尔问题第一次真正出现是在1975
This guy named Steve Selvin at Berkeley presented the problem in The American Statistician.
伯克利大学一名叫史蒂夫·塞尔温的家伙把这个问题难登在了《美国统计学者》杂志上
Selvin contested that the odds was 2/3 and no one argued with him.
塞尔温说选到山羊的概率是2/3,当时没有人跟他争辩
And you know, over the next 15 years, multiple other academics reiterated the same problem
在接下来的15年里,很多学者反复讨论了这一问题
and no one ever told them that they were wrong.
还是没有人说他们错了
Then in 1990 Marilyn answered the same question correctly and people went bananas.
但1990年玛丽莲说出这个问题的正确答案时,大家都疯了
Marilyn ended up tallying up what percentage of the 10,000 responses claimed she was wrong.
玛丽莲统计了那1万封反馈信里说她搞错了的人的概率
Only 8% of readers actually agreed with her
只有8%的读者同意她的看法
and after subsequent columns, she was able to raise that to only 56%.
即便她后来开了专栏解释这个问题,这一比例也只上升到了56%
And among academics: It was 35% among academics initially supporting the answer.
学术界呢:当初只35%的学者支持她的答案
And about 70% of academics ultimately decided to agree with her.
最后也只有70%的学者选择同意她的看法
The only way she managed to get people on her side was by asking them to do the experiment themselves.
玛丽莲只能靠让人们亲自做这个实验说服大家站到她一边
Elementary, middle school, and high school teachers from all over the country wrote in,
全国上下的小学、初中、高中老师纷纷来信
astounded that their students were able to prove her right.
因为令他们震惊的是,他们的学生竟然能证明玛丽莲是正确的
It’s easy now to do a simple google search of this little sucker of a problem
现在,我们轻轻松松就能在谷歌上搜到
and get a million explanations on how to arrive at the right answer.
各种各样解答这个问题的办法
There's something about this problem that really strikes a chord with, not only statisticians,
重点是,这个问题不仅仅能让统计学者们产生共鸣
but just everyday problem solvers and people.
还能让处理日常问题的普罗大众产生共鸣


