一、选择题(本大题共10小题,每小题4分,共40分)每题的选项中只有一项符合题目要求.
1.(4分)(2013•乌鲁木齐)|﹣2|的相反数是( )
A. ﹣2 B. ﹣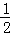 C.
C.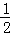 D. 2
D. 2
考点: 绝对值;相反数.
分析: 相反数的意义:一个正数的相反数是负数,一个负数的相反数是正数,0的相反数是0.
绝对值规律总结:一个正数的绝对值是它本身,一个负数的绝对值是它的相反数,0的绝对值是0.
解答: 解:∵|﹣2|=2,
∴2的相反数是﹣2.
故选A.
点评: 本题考查了相反数的意义及绝对值的性质:学生易把相反数的意义与倒数的意义混淆.
2.(4分)(2013•乌鲁木齐)下列运算正确的是( )
A. a4+a2=a6 B. 5a﹣3a=2 C. 2a3•3a2=6a6 D. (﹣2a)﹣2=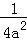
考点: 单项式乘单项式;合并同类项;负整数指数幂.
分析: 根据单项式乘单项式、合并同类项、负整数指数幂的运算法则,分别进行计算,即可得出答案.
解答: 解:A、a4+a2不能合并,故本选项错误;
B、5a﹣3a=2a,故本选项错误;
C、2a3•3a2=6a5,故本选项错误;
D、(﹣2a)﹣2=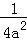 故本选项正确;
故本选项正确;
故选D.
点评: 此题考查了单项式乘单项式、合并同类项、负整数指数幂,解题的关键是熟练掌握运算法则,注意指数的变化情况.
3.(4分)(2013•乌鲁木齐)如图是某几何体的三视图,则该几何体的体积是( )
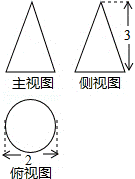
A. π B. 2π C. 3π D. 4π
考点: 圆锥的计算;由三视图判断几何体.
专题: 计算题.
分析: 先根据三视图得到该几何体为圆锥,并且圆锥的底面圆的半径为1,高为3,然后根据圆锥的体积公式求解.
解答: 解:根据三视图得该几何体为圆锥,圆锥的底面圆的半径为1,高为3,
所以圆锥的体积=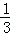 ×π×12×3=π.
×π×12×3=π.
故选A.
点评: 本题考查了圆锥的计算:圆锥的侧面展开图为扇形,扇形的弧长等于圆锥底面圆的周长,扇形的半径等于圆锥的母线长.也考查了三视图.
4.(4分)(2013•乌鲁木齐)若关于x的方程式x2﹣x+a=0有实根,则a的值可以是( )
A. 2 B. 1 C. 0.5 D. 0.25
考点: 根的判别式.
分析: 根据判别式的意义得到△=(﹣1)2﹣4a≥0,然后解不等式,最后根据不等式的解集进行判断.
解答: 解:根据题意得△=(﹣1)2﹣4a≥0,
解得m≤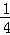 .
.
故选D.
点评: 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2﹣4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.
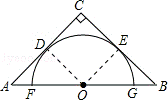
5.(4分)(2013•乌鲁木齐)如图,半圆O与等腰直角三角形两腰CA、CB分别切于D、E两点,直径FG在AB上,若BG=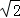 ﹣1,则△ABC的周长为( )
﹣1,则△ABC的周长为( )
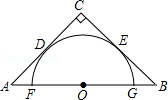
A. 4+2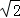 B. 6 C. 2+2
B. 6 C. 2+2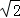 D. 4
D. 4
考点: 切线的性质.
分析: 首先连接OD,OE,易证得四边形ODCE是正方形,△OEB是等腰直角三角形,首先设OE=r,由OB=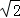 OE=
OE=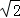 r,可得方程:
r,可得方程: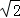 ﹣1+r=
﹣1+r=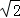 r,解此方程,即可求得答案.
r,解此方程,即可求得答案.
解答: 解:连接OD,OE,
∵半圆O与等腰直角三角形两腰CA、CB分别切于D、E两点,
∴∠C=∠OEB=∠OEC=∠ODC=90°,
∴四边形ODCE是矩形,
∵OD=OE,
∴四边形ODCE是正方形,
∴CD=CE=OE,
∵∠A=∠B=45°,
∴△OEB是等腰直角三角形,
设OE=r,
∴BE=OG=r,
∴OB=OG+BG=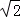 ﹣1+r,
﹣1+r,
∵OB=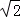 OE=
OE=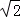 r,
r,
∴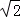 ﹣1+r=
﹣1+r=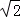 r,
r,
∴r=1,
∴AC=BC=2r=2,AB=2OB=2×(1+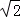 ﹣1)=2
﹣1)=2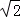 .
.
∴△ABC的周长为:AC+BC+AB=4+2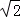 .
.
故选A.
点评: 此题考查了切线的性质、正方形的判定与性质以及等腰直角三角形的性质.此题难度适中,注意掌握辅助线的作法,注意数形结合思想与方程思想的应用.
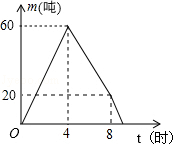
6.(4分)(2013•乌鲁木齐)某仓库调拨一批物资,调进物资共用8小时,调进物资4小时后同时开始调出物资(调进与调出的速度保持不变).该仓库库存物资m(吨)与时间t(小时)之间的函数关系如图所示.则这批物资从开始调进到全部调出所需要的时间是( )
A. 8.4小时 B. 8.6小时 C. 8.8小时 D. 9小时
考点: 函数的图象.
分析: 通过分析题意和图象可求调进物资的速度,调出物资的速度;从而可计算最后调出物资20吨所花的时间.
解答: 解:调进物资的速度是60÷4=15吨/时,
当在第4小时时,库存物资应该有60吨,在第8小时时库存20吨,
所以调出速度是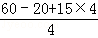 =25吨/时,
=25吨/时,
所以剩余的20吨完全调出需要20÷25=0.8小时.
故这批物资从开始调进到全部调出需要的时间是8+0.8=8.8小时.
故选C.
点评: 此题主要考查了函数图象,要能根据函数图象的性质和图象上的数据分析得出函数的类型和所需要的条件,结合实际意义得到正确的结论.
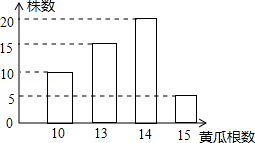
7.(4分)(2013•乌鲁木齐)种植能手李大叔种植了一批新品种黄瓜,为了考察这种黄瓜的生长情况,李大叔抽查了部分黄瓜株上长出的黄瓜根数,得到如图的条形图,则抽查的这部分黄瓜株上所结黄瓜根数的中位数和众数分别是( )
A. 13.5,20 B. 15,5 C. 13.5,14 D. 13,14
考点: 众数;条形统计图;中位数.
分析: 一组数据中出现次数最多的数据叫做众数,结合直方图即可得出众数,中位数.
解答: 解:接黄瓜14根的最多,故众数为14;
总共50株,中位数落在第25、26株上,分别是13,14,故中位数为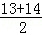 =13.5.
=13.5.
故选C.
点评: 本题考查了众数、中位数及条形统计图的知识,解答本题的关键是理解众数、中位数的定义,能看懂统计图.
8.(4分)(2013•乌鲁木齐)对平面上任意一点(a,b),定义f,g两种变换:f(a,b)=(a,﹣b).如f(1,2)=(1,﹣2);g(a,b)=(b,a).如g(1,2)=(2,1).据此得g(f(5,﹣9))=( )
A. (5,﹣9) B. (﹣9,﹣5) C. (5,9) D. (9,5)
考点: 点的坐标.
专题: 新定义.
分析: 根据两种变换的规则,先计算f(5,﹣9)=(5,9),再计算g(5,9)即可.
解答: 解:g(f(5,﹣9))=g(5,9)=(9,5).
故选D.
点评: 本题考查了点的坐标,理解新定义的变化规则是解题的关键.
9.(4分)(2013•乌鲁木齐)如图所示的数码叫“莱布尼茨调和三角形”,它们是由整数的倒数组成的,第n行有n个数,且两端的数均为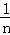 ,每个数是它下一行左右相邻两数的和,则第8行第3个数(从左往右数)为( )
,每个数是它下一行左右相邻两数的和,则第8行第3个数(从左往右数)为( )
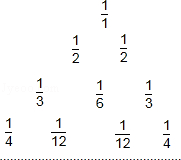
A.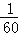 B.
B.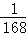 C.
C.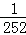 D.
D.
考点: 规律型:数字的变化类.
分析: 根据“莱布尼兹调和三角形”的特征,每个数是它下一个行左右相邻两数的和,得出将杨晖三角形中的每一个数Cnr都换成分数得到莱布尼兹三角形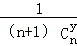 ,得到一个莱布尼兹三角形,从而可求出第n(n≥3)行第3个数字,进而可得第8行第3个数.
,得到一个莱布尼兹三角形,从而可求出第n(n≥3)行第3个数字,进而可得第8行第3个数.
解答: 解:将杨晖三角形中的每一个数Cnr都换成分数,得到莱布尼兹三角形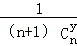 ,
,
杨晖三角形中第n(n≥3)行第3个数字是Cn﹣12,
则“莱布尼兹调和三角形”第n(n≥3)行第3个数字是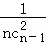 =
=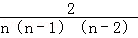 ,
,
则第8行第3个数(从左往右数)为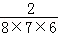 =
=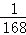 ;
;
故选B.
点评: 本题考查了数字的变化类,解题的关键是通过观察、分析、归纳推理,得出各数的关系,找出规律.
10.(4分)(2013•乌鲁木齐)已知m,n,k为非负实数,且m﹣k+1=2k+n=1,则代数式2k2﹣8k+6的最小值为( )
A. ﹣2 B. 0 C. 2 D. 2.5
考点: 二次函数的最值.
分析: 首先求出k的取值范围,进而利用二次函数增减性得出k=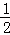 时,代数式2k2﹣8k+6的最小值求出即可.
时,代数式2k2﹣8k+6的最小值求出即可.
解答: 解:∵m,n,k为非负实数,且m﹣k+1=2k+n=1,
∴m,n,k最小为0,当n=0时,k最大为: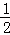 ,
,
∴0≤k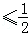 ,
,
∵2k2﹣8k+6=2(k﹣2)2﹣2,
∴a=2>0,∴k≤2时,代数式2k2﹣8k+6的值随x的增大而减小,
∴k=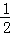 时,代数式2k2﹣8k+6的最小值为:2×(
时,代数式2k2﹣8k+6的最小值为:2×(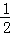 )2﹣8×
)2﹣8×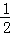 +6=2.5.
+6=2.5.
故选:D.
点评: 此题主要考查了二次函数的最值求法以及二次函数增减性等知识,根据二次函数增减性得出k=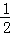 时,代数式2k2﹣8k+6的最小值是解题关键.
时,代数式2k2﹣8k+6的最小值是解题关键.












