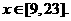一.选择题
(1) A (2) D (3) C (4) A (5) A (6) B
(7) C (8) D (9) C (10) B (11) A (12) C
二.填空题
(13)  (14)
(14) 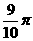 (15) 140 (16) 10
(15) 140 (16) 10
三.解答题
(17) 解:
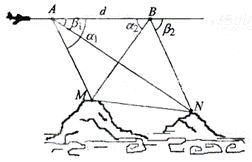
方案一:①需要测量的数据有:A点到M,N点的俯角 ;B点到M,N的俯角
;B点到M,N的俯角 ;A,B的距离 d (如图)
;A,B的距离 d (如图)
所示) . ……….3分
②第一步:计算AM . 由正弦定理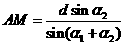 ;
;
第二步:计算AN . 由正弦定理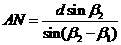 ;
;
第三步:计算MN. 由余弦定理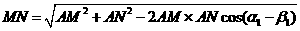 .
.
方案二:①需要测量的数据有:
A点到M,N点的俯角 ,
, ;B点到M,N点的府角
;B点到M,N点的府角 ,
, ;A,B的距离 d (如图所示).
;A,B的距离 d (如图所示).
②第一步:计算BM . 由正弦定理 ;
;
第二步:计算BN . 由正弦定理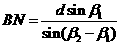 ;
; 

第三步:计算MN . 由余弦定理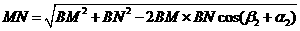
(18) 解:
(Ⅰ)甲、乙被抽到的概率均为 ,且事件“甲工人被抽到”与事件“乙工人被抽到”相互独立,故甲、乙两工人都被抽到的概率为
,且事件“甲工人被抽到”与事件“乙工人被抽到”相互独立,故甲、乙两工人都被抽到的概率为 
 .
.
(Ⅱ)(i)由题意知A类工人中应抽查25名,B类工人中应抽查75名.
故 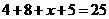 ,得
,得 ,
,
 ,得
,得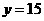 .
.
频率分布直方图如下
从直方图可以判断:B类工人中个体间的关异程度更小 .
(ii) 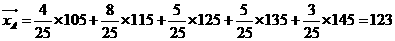 ,
,
 ,
,

A类工人生产能力的平均数,B类工人生产能力的平均数以及全工厂工人生产能力的平均数的会计值分别为123,133.8和131.1 .

(19)解法一:
(Ⅰ)连BD,设AC交BD于O,由题意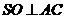 。在正方形ABCD中,
。在正方形ABCD中,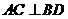 ,所以
,所以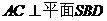 ,得
,得 .
.
(Ⅱ)设正方形边长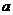 ,则
,则 。
。
又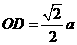 ,所以
,所以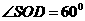 ,
,
连 ,由(Ⅰ)知
,由(Ⅰ)知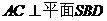 ,所以
,所以 ,
, 
且 ,所以
,所以 是二面角
是二面角 的平面角。
的平面角。
由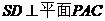 ,知
,知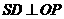 ,所以
,所以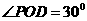 ,
,
即二面角 的大小为
的大小为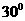 。
。
(Ⅲ)在棱SC上存在一点E,使
由(Ⅱ)可得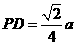 ,故可在
,故可在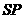 上取一点
上取一点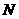 ,使
,使 ,过
,过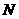 作
作 的平行线与
的平行线与 的交点即为
的交点即为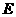 。连BN。在
。连BN。在 中知
中知 ,又由于
,又由于 ,故平面
,故平面 ,得
,得 ,由于
,由于 ,故
,故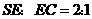 .
.
解法二:
(Ⅰ);连 ,设
,设 交于
交于 于
于 ,由题意知
,由题意知 .以O为坐标原点,
.以O为坐标原点, 分别为
分别为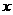 轴、
轴、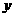 轴、
轴、 轴正方向,建立坐标系
轴正方向,建立坐标系 如图。
如图。
设底面边长为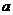 ,则高
,则高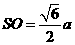 。
。
于是 
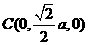

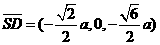
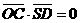

故 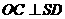
从而 
(Ⅱ)由题设知,平面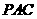 的一个法向量
的一个法向量 ,平面
,平面 的一个法向量
的一个法向量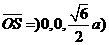 ,设所求二面角为
,设所求二面角为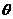 ,则
,则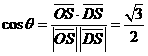 ,所求二面角的大小为
,所求二面角的大小为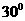
(Ⅲ)在棱 上存在一点
上存在一点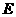 使
使 .
.
由(Ⅱ)知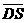 是平面
是平面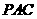 的一个法向量,
的一个法向量,
且 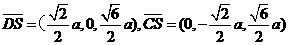
设 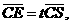

则 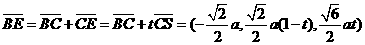
而 
即当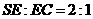 时,
时,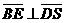
而 不在平面
不在平面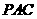 内,故
内,故
(20)解:
(Ⅰ)设椭圆长半轴长及半焦距分别为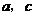 ,由已知得
,由已知得
 ,
, 
所以椭圆 的标准方程为
的标准方程为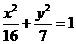
(Ⅱ)设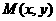 ,其中
,其中 。由已知
。由已知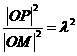 及点
及点 在椭圆
在椭圆 上可得
上可得
 。
。
整理得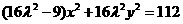 ,其中
,其中 。
。
(i)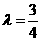 时。化简得
时。化简得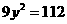

所以点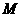 的轨迹方程为
的轨迹方程为 ,轨迹是两条平行于
,轨迹是两条平行于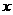 轴的线段。
轴的线段。
(ii)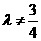 时,方程变形为
时,方程变形为 ,其中
,其中
当 时,点
时,点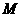 的轨迹为中心在原点、实轴在
的轨迹为中心在原点、实轴在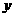 轴上的双曲线满足
轴上的双曲线满足 的部分。
的部分。
当 时,点
时,点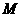 的轨迹为中心在原点、长轴在
的轨迹为中心在原点、长轴在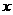 轴上的椭圆满足
轴上的椭圆满足 的部分;
的部分;
当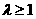 时,点
时,点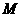 的轨迹为中心在原点、长轴在
的轨迹为中心在原点、长轴在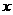 轴上的椭圆;
轴上的椭圆;
(21)解:
(Ⅰ)当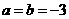 时,
时,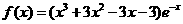 ,故
,故
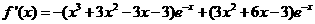

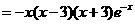

当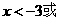
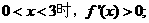
当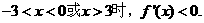
从而 单调减少.
单调减少.
(Ⅱ)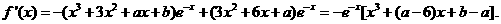
由条件得: 从而
从而

因为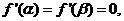 所以
所以
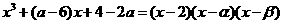
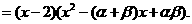
将右边展开,与左边比较系数得, 故
故
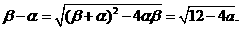
又 由此可得
由此可得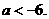
于是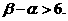

(22)解:
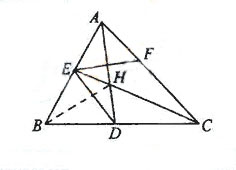
(Ⅰ)在△ABC中,因为∠B=60°,
所以∠BAC+∠BCA=120°.
因为AD,CE是角平分线,
所以∠HAC+∠HCA=60°,
故∠AHC=120°.
于是∠EHD=∠AHC=120°.
因为∠EBD+∠EHD=180°,
所以B,D,H,E四点共圆.
(Ⅱ)连结BH,则BH为∠ABC的平分线,得∠HBD=30°
由(Ⅰ)知B,D,H,E四点共圆,
所以∠CED=∠HBD=30°.
又∠AHE=∠EBD=60°,由已知可得EF⊥AD,
可得∠CEF=30°.
所以CE平分∠DEF. 
(23)解:
(Ⅰ)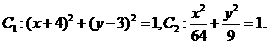
 为圆心是(
为圆心是( ,半径是1的圆.
,半径是1的圆.
 为中心是坐标原点,焦点在x轴上,长半轴长是8,短半轴长是3的椭圆.
为中心是坐标原点,焦点在x轴上,长半轴长是8,短半轴长是3的椭圆.
(Ⅱ)当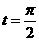 时,
时,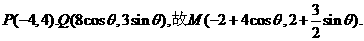
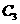 为直线
为直线
从而当 时,
时,
(24)解:
(Ⅰ)
(Ⅱ)依题意,x满足
{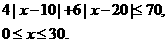
解不等式组,其解集为【9,23】
所以