1. The sides of a rectangular piece of card are each 10 per cent too long for a particular project. By what percentage is the area too large?
2. Andy, Mark and Sean all have their birthdays today, but Andy is more than twice as old as Mark and Mark is more than four years older than Sean. If Andy is less than 16 years old, what is one possible value for Mark's age in years ?
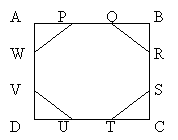
3. ABCD is a square. Also AP=PQ=QB=BR=RS=SC=CT=TU=UD=DV=VW=WA. The area of the octagon PQRSTUVW is what fraction of the square?
4. Triangle ABC is a right angled triangle. Also AC = 5, CB = 3 and angle ADB is a right angle.
What is the length of DB?
5. A football team has won 10 games and lost 5 games. If the team wins the remaining games of the season, it will have won 80 percent of its games. How many games in total will have been played?
6. Let the function f be defined by f(x) = x - 1
What is the value of y if y is a positive integer such that 1/3 f(y²) = 5?
7. The amount of time taken to paint a wall is inversely proportional to the number of painters working on the job. If it takes 3 painters 5 days to complete such a job, how many days longer will it take if there are only 2 painters working?
8. Line l and line m lie in the same plane but have no points in common. They are both tangent to a circle of area 9π. What is the shortest distance between any point on l and any point on m?
9. A box contains 5 chocolates with soft centers, 6 with nut centers, and 11 with hard caramel centers. Three students take turns to take a chocolate at random from the box and eat it. If the probability that all three students take soft centers is 1/x, what is the value of x?
10. At one point in a game the shooting team has a ratio of hits to misses of 5:1. After the next team misses the nest three shots, which are the last in the game, its ratio of hits to misses is 5:2. What is the total number of shots taken by the team in the game?












