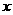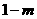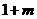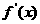20.(本小题满分12分)
已知等差数列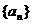 的公差d不为0,设
的公差d不为0,设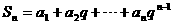
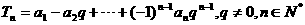
(Ⅰ)若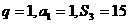 ,求数列
,求数列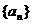 的通项公式;
的通项公式;
(Ⅱ)若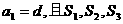 成等比数列,求q的值。
成等比数列,求q的值。
(Ⅲ)若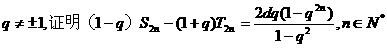
【答案】(1)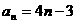 (2)
(2)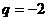 (3)略
(3)略
【解析】 (1)解:由题设,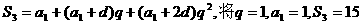
代入解得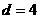 ,所以
,所以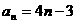
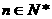
(2)解:当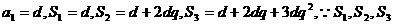 成等比数列,所以
成等比数列,所以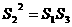 ,即
,即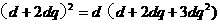 ,注意到
,注意到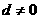 ,整理得
,整理得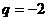
(3)证明:由题设,可得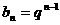 ,则
,则
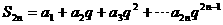 ①
①
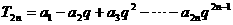 ②
②
①-②得,
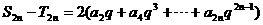
①+②得,
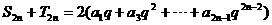 ③
③
③式两边同乘以 q,得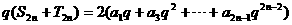
所以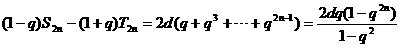
(3)证明: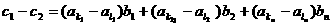
=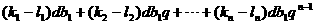
因为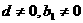 ,所以
,所以
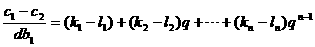
若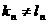 ,取i=n,
,取i=n,
若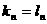 ,取i满足
,取i满足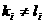 ,且
,且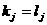 ,
,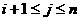
由(1)(2)及题设知,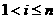 ,且
,且
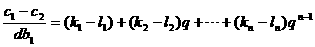
① 当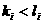 时,
时,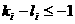 ,由
,由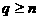 ,
,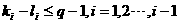
即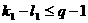 ,
,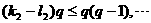
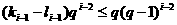
所以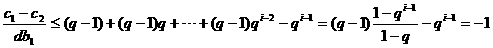
因此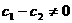
② 当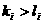 时,同理可得
时,同理可得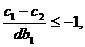 因此
因此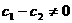
综上,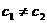
【考点定位】本小题主要考查了等差数列的通项公式,等比数列通项公式与前n项和等基本知识,考查运算能力和推理论证能力和综合分析解决问题的能力。
21. (本小题满分12分)
设函数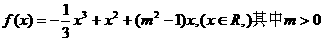
(Ⅰ)当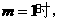 曲线
曲线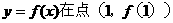 处的切线斜率
处的切线斜率
(Ⅱ)求函数的单调区间与极值;
(Ⅲ)已知函数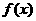 有三个互不相同的零点0,
有三个互不相同的零点0,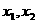 ,且
,且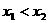 。若对任意的
。若对任意的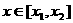 ,
,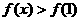 恒成立,求m的取值范围。
恒成立,求m的取值范围。
【答案】(1)1(2)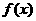 在
在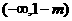 和
和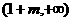 内减函数,在
内减函数,在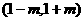 内增函数。函数
内增函数。函数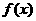 在
在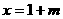 处取得极大值
处取得极大值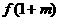 ,且
,且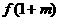 =
=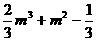
函数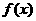 在
在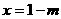 处取得极小值
处取得极小值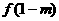 ,且
,且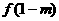 =
=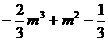
【解析】解:当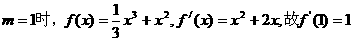
所以曲线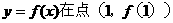 处的切线斜率为1.
处的切线斜率为1.
(2)解: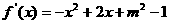 ,令
,令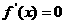 ,得到
,得到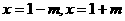
因为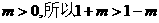
当x变化时,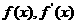 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
| + | 0 | - | 0 | + |
|
| 极小值 |
| 极大值 |
|
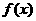 在
在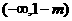 和
和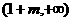 内减函数,在
内减函数,在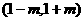 内增函数。
内增函数。
函数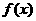 在
在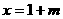 处取得极大值
处取得极大值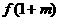 ,且
,且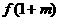 =
=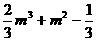
函数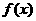 在
在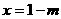 处取得极小值
处取得极小值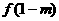 ,且
,且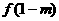 =
=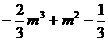
(3)解:由题设, 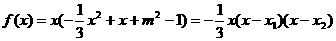
所以方程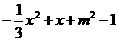 =0由两个相异的实根
=0由两个相异的实根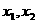 ,故
,故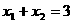 ,且
,且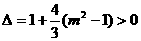 ,解得
,解得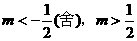
因为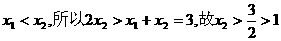
若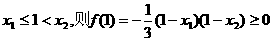 ,而
,而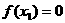 ,不合题意
,不合题意
若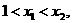 则对任意的
则对任意的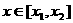 有
有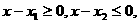
则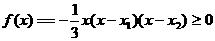 又
又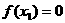 ,所以函数
,所以函数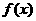 在
在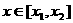 的最小值为0,于是对任意的
的最小值为0,于是对任意的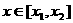 ,
,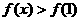 恒成立的充要条件是
恒成立的充要条件是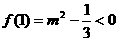 ,解得
,解得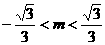
综上,m的取值范围是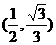
【考点定位】本小题主要考查导数的几何意义,导数的运算,以及函数与方程的根的关系解不等式等基础知识,考查综合分析问题和解决问题的能力。
22. (本小题满分14分)
已知椭圆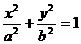 (
(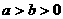 )的两个焦点分别为
)的两个焦点分别为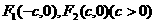 ,过点
,过点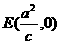 的直线与椭圆相交于点A,B两点,且
的直线与椭圆相交于点A,B两点,且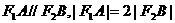
(Ⅰ求椭圆的离心率
(Ⅱ)直线AB的斜率;
(Ⅲ)设点C与点A关于坐标原点对称,直线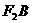 上有一点H(m,n)(
上有一点H(m,n)(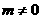 )在
)在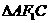 的外接圆上,求
的外接圆上,求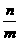 的值。
的值。
【答案】(1)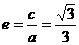 (2)
(2)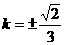 (3)
(3)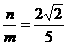
【解析】 (1)解:由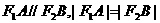 ,得
,得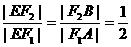 ,从而
,从而
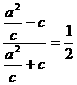 ,整理得
,整理得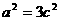 ,故离心率
,故离心率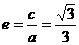
(2)解:由(1)知,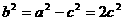 ,所以椭圆的方程可以写为
,所以椭圆的方程可以写为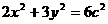
设直线AB的方程为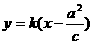 即
即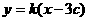
由已知设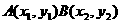 则它们的坐标满足方程组
则它们的坐标满足方程组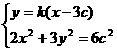
消去y整理,得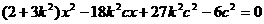
依题意,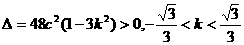
而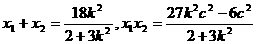 ,有题设知,点B为线段AE的中点,所以
,有题设知,点B为线段AE的中点,所以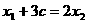
联立三式,解得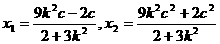 ,将结果代入韦达定理中解得
,将结果代入韦达定理中解得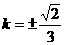
(3)由(2)知,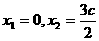 ,当
,当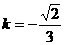 时,得A
时,得A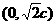 由已知得
由已知得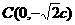
线段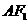 的垂直平分线l的方程为
的垂直平分线l的方程为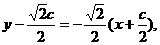 直线l与x轴的交点
直线l与x轴的交点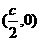 是
是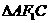 的外接圆的圆心,因此外接圆的方程为
的外接圆的圆心,因此外接圆的方程为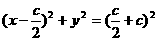
直线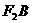 的方程为
的方程为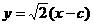 ,于是点
,于是点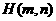 满足方程组
满足方程组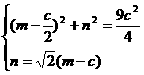 由
由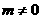 ,解得
,解得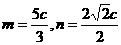 ,故
,故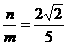
当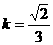 时,同理可得
时,同理可得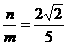
【考点定位】本小题主要考查椭圆的标准方程和几何性质,直线方程,圆的方程等基础知识。考查用代数方法研究圆锥曲线的性质和数形结合的思想,考查运算能力和推理能力。