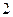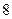第Ⅰ卷(选择题 共50分)
一、选择题:本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的。
(1)复数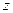 满足
满足 ,则
,则 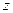 =
=
(A)  (B)
(B) 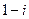
(C) 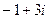
 (D)
(D)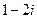
【解析】选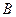
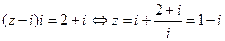
(2)设集合A={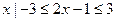 },集合B为函数
},集合B为函数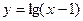 的定义域,
的定义域, 则A
则A B=
B=
(A) (1,2)(B)[1,2]
(C)[ 1,2) (D)(1,2 ]
【解析】选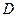
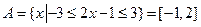 ,
,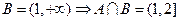
(3)(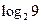 )·(
)·(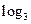 4)=
4)=
(A)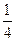
 (B)
(B)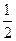
(C)2(D) 4
【解析】选
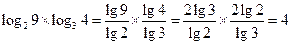
(4)命题“存在实数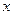 ,使
,使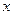 > 1”的否定是
> 1”的否定是
(A) 对任意实数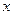 , 都有
, 都有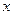 > 1(B)不存在实数
> 1(B)不存在实数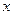 ,使
,使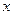
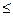 1
1
(C) 对任意实数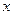 , 都有
, 都有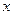
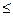 1(D)存在实数
1(D)存在实数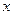 ,使
,使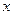
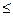 1
1
【解析】选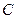
存在---任意,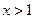 ---
---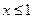
(5)公比为2的等比数列{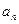 } 的各项都是正数,且
} 的各项都是正数,且 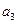
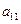 =16,则
=16,则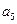 =
=
(A) 1 (B)2
(C) 4(D)8
【解析】选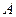
(6)如图所示,程序框图(算法流程图)的输出结果是
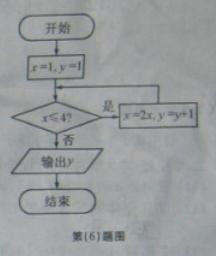
(A) 3(B)4
(C) 5(D)8
【解析】选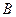
|
|
|
|
|
|
|
|
|
|
(7)要得到函数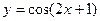 的图象,只要将函数
的图象,只要将函数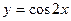 的图象
的图象
(A) 向左平移1个单位
(B) 向右平移1个单位
(C) 向左平移 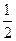 个单位
个单位
(D) 向右平移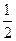 个单位
个单位
【解析】选
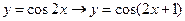 左+1,平移
左+1,平移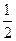
(8)若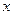 ,
,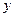 满足约束条件
满足约束条件 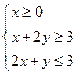 ,则
,则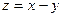 的最小值是
的最小值是
(A) -3 (B)0
(C) 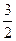 (D)3
(D)3
【解析】选
【解析】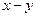 的取值范围为
的取值范围为
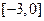
约束条件对应 边际及内的区域:
边际及内的区域: 则
则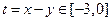
(9)若直线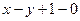 与圆
与圆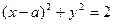 有公共点,则实数
有公共点,则实数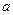 取值范围是
取值范围是
(A) [-3 ,-1 ](B)[ -1 , 3 ]
(C) [ -3 ,1 ](D)(- 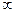 ,-3 ]U[
,-3 ]U[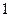 ,+
,+ 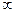 )
)
【解析】选
圆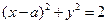 的圆心
的圆心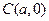 到直线
到直线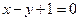 的距离为
的距离为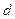
则 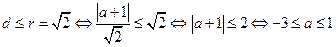
(10)袋中共有6个除了颜色外完全相同的球,其中有1个红球,2个白球和3个黑球,从袋中任取两球,两球颜色为一白一黑的概率等于
(A)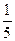 (B)
(B)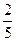
(C)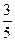 (D)
(D)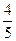
【解析】选
1个红球,2个白球和3个黑球记为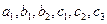
从袋中任取两球共有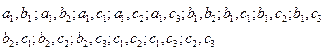 15种;
15种;
满足两球颜色为一白一黑有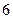 种,概率等于
种,概率等于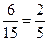
第Ⅱ卷(非选择题 共100分)
二.填空题:本大题共5小题,每小题5分,共25分,把答案填在答题卡的相应位置。
(11)设向量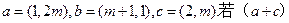 ⊥
⊥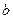 ,则|
,则|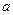 |=____________.【解析】
|=____________.【解析】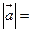

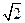
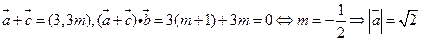
12某几何体的三视图如图所示,则该几何体的体积等于______.
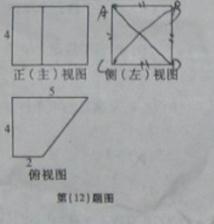
【解析】表面积是
该几何体是底面是直角梯形,高为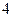 的直四棱柱
的直四棱柱
几何体的的体积是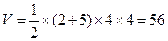
(13)若函数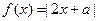 的单调递
的单调递 增区间是
增区间是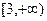 ,则
,则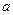 =________.
=________.
【解析】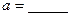
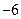
由对称性: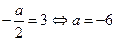
(14)过抛物线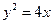 的焦点
的焦点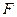 的直线交该抛物线于
的直线交该抛物线于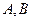 两点,若
两点,若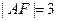 ,则
,则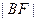 =______。
=______。
【解析】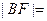

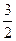
设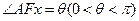 及
及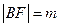 ;则点
;则点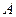 到准线
到准线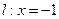 的距离为
的距离为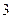
得: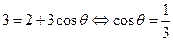 又
又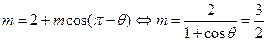
(15)若四面体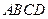 的三组对棱分别
的三组对棱分别 相等,即
相等,即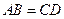 ,
,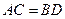 ,
,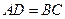 ,则______
,则______ __(写出所有正确结论编号)。
__(写出所有正确结论编号)。
①四 面体
面体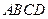 每组对棱相互垂直
每组对棱相互垂直
②四面体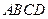 每个面的面积相等
每个面的面积相等
③从四面体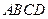 每个顶点出发的三条棱两两夹角之和大于
每个顶点出发的三条棱两两夹角之和大于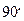 而小于
而小于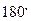
④连接四面体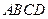 每组对棱中点的线段互垂直平分
每组对棱中点的线段互垂直平分
⑤从四面体 每个顶点出发的三条棱的长可作为一个三角形的三边长
每个顶点出发的三条棱的长可作为一个三角形的三边长
【解析】正确的是 ②④⑤
②④⑤
②四面体 每个面是全等三角形,面积相等
每个面是全等三角形,面积相等
③从四面体 每个顶点出发的三条棱两两夹角之和等于
每个顶点出发的三条棱两两夹角之和等于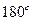
④连接四面体 每组对棱中点构成菱形,线段互垂直平分
每组对棱中点构成菱形,线段互垂直平分
⑤从四面体 每个顶点出发的三条棱的长可作为一个三角形的三边长
每个顶点出发的三条棱的长可作为一个三角形的三边长