一、选择题(本大题共12小题,每小题3分,共36分)每小题都给出标号为(A)、(B)、(C)、(D)的四个选项,其中只有一个是正确的。请考生用2B铅笔在答题卡上将选定的答案标号涂黑。
1.(3分)(2013•贵港)﹣3的绝对值是( )
A. ﹣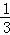 B.
B. 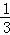 C. ﹣3 D. 3
C. ﹣3 D. 3
考点: 绝对值.
分析: 根据绝对值的性质计算即可得解.
解答: 解:﹣3的绝对值是3,
即|﹣3|=3.
故选D.
点评: 本题考查了绝对值的性质,负数的绝对值等于它的相反数.
2.(3分)(2013•贵港)纳米是非常小的长度单位,1纳米=10﹣9米.某种病菌的长度约为50纳米,用科学记数法表示该病菌的长度,结果正确的是( )
A. 5×10﹣10米 B. 5×10﹣9米 C. 5×10﹣8米 D. 5×10﹣7米
考点: 科学记数法—表示较小的数.
分析: 绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10﹣n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.
解答: 解:50纳米=50×10﹣9米=5×10﹣8米.
故选C.
点评: 本题考查用科学记数法表示较小的数,一般形式为a×10﹣n,其中1≤|a|<10,n为由原数左边起第一个不为零的数字前面的0的个数所决定.
3.(3分)(2013•贵港)下列四种调查:
①调查某班学生的身高情况;
②调查某城市的空气质量;
③调查某风景区全年的游客流量;
④调查某批汽车的抗撞击能力.
其中适合用全面调查方式的是( )
A. ① B. ② C. ③ D. ④
考点: 全面调查与抽样调查.
分析: 调查方式的选择需要将普查的局限性和抽样调查的必要性结合起来,具体问题具体分析,普查结果准确,所以在要求精确、难度相对不大,实验无破坏性的情况下应选择普查方式,当考查的对象很多或考查会给被调查对象带来损伤破坏,以及考查经费和时间都非常有限时,普查就受到限制,这时就应选择抽样调查.
解答: 解:①调查某班学生的身高情况,由于人数少,范围小,可以采用全面调查的方式,故选项正确;
②调查某城市的空气质量,由于工作量大,不便于检测,采用抽样调查,故选项错误;
③调查某风景区全年的游客流量,由于人数多,工作量大,采用抽样调查,故选项错误;
④调查某批汽车的抗撞击能力,由于具有破坏性,应当使用抽样调查,故选项错误.
故选A.
点评: 本题主要考查了抽样调查和全面调查,由普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似,难度适中.
4.(3分)(2013•贵港)下列四个式子中,x的取值范围为x≥2的是( )
A. 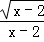 B.
B. 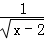 C.
C. 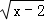 D.
D. 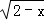
考点: 二次根式有意义的条件;分式有意义的条件.
分析: 根据分式有意义的条件是分母不等于零,二次根式中的被开方数是非负数分别进行分析即可.
解答: 解:A、x﹣2≥0,且x﹣2≠0,解得:x>2,故此选项错误;
B、x﹣2>0,解得:x>2,故此选项错误;
C、x﹣2≥0,解得x≥2,故此选项正确;
D、2﹣x≥0,解得x≤2,故此选项错误;
故选:C.
点评: 此题主要考查了二次根式有意义的条件,以及分式有意义的条件,题目比较基础.
5.(3分)(2013•贵港)下列计算结果正确的是( )
A. 3a﹣(﹣a)=2a B. a3×(﹣a)2=a5 C. a5÷a=a5 D. (﹣a2)3=a6
考点: 同底数幂的除法;整式的加减;同底数幂的乘法;幂的乘方与积的乘方.
专题: 计算题.
分析: 根据同底数幂的除法,底数不变指数相减;合并同类项,系数相加字母和字母的指数不变;同底数幂的乘法,底数不变指数相加;幂的乘方,底数不变指数相乘,对各选项计算后利用排除法求解.
解答: 解:A、由于3a+a=4a≠2a,故本选项错误;
B、由于a3×(﹣a)2=a3×a2=a5,故本选项正确;
C、由于a5÷a=a5﹣1=a4≠a5,故本选项错误;
D、由于(﹣a2)3=﹣a6,故本选项错误.
故选B.
点评: 本题考查同底数幂的除法,合并同类项,同底数幂的乘法,幂的乘方很容易混淆,一定要记准法则才能做题.
6.(3分)(2013•贵港)如图是一个小正方体的展开图,把展开图折叠成小正方体后,有“共”字一面的相对面上的字是( )

A. 美 B. 丽 C. 家 D. 园
考点: 专题:正方体相对两个面上的文字.
分析: 正方体的表面展开图,相对的面之间一定相隔一个正方形,根据这一特点作答.
解答: 解:正方体的表面展开图,相对的面之间一定相隔一个正方形,
“共”与“园”是相对面,
“建”与“丽”是相对面,
“美”与“家”是相对面.
故选D.
点评: 本题主要考查了正方体相对两个面上的文字,注意正方体的空间图形,从相对面入手,分析及解答问题.
7.(3分)(2013•贵港)下列四个命题中,属于真命题的是( )
A. 若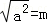 ,则a=m B. 若a>b,则am>bm
,则a=m B. 若a>b,则am>bm
C. 两个等腰三角形必定相似 D. 位似图形一定是相似图形
考点: 命题与定理
分析: 根据二次根式的性质,不等式的基本性质,相似三角形与相似图形的判定对各选项分析判断后利用排除法求解.
解答: 解:A、若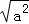 =m,则|a|=m,故本选项错误;
=m,则|a|=m,故本选项错误;
B、若a>b,m>0,则am>bm,故本选项错误;
C、两个等腰三角形两腰对应成比例,夹角顶角不一定相等,所以两三角形不一定相似,故本选项错误;
D、位似图形一定是相似图形是真命题,故本选项正确.
故选D.
点评: 本题主要考查命题的真假判断,正确的命题叫真命题,错误的命题叫做假命题.判断命题的真假关键是要熟悉课本中的性质定理.
8.(3分)(2013•贵港)关于x的分式方程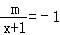 的解是负数,则m的取值范围是( )
的解是负数,则m的取值范围是( )
A. m>﹣1 B. m>﹣1且m≠0 C. m≥﹣1 D. m≥﹣1且m≠0
考点: 分式方程的解.
分析: 由题意分式方程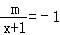 的解为负数,解方程求出方程的解x,然后令其小于0,解出m的范围.注意最简公分母不为0.
的解为负数,解方程求出方程的解x,然后令其小于0,解出m的范围.注意最简公分母不为0.
解答: 解:方程两边同乘(x+1),得m=﹣x﹣1
解得x=﹣1﹣m,
∵x<0,
∴﹣1﹣m<0,
解得m>﹣1,
又x+1≠0,
∴﹣1﹣m+1≠0,
∴m≠0,
即m>﹣1且m≠0.
故选B.
点评: 此题主要考查分式的解,关键是会解出方程的解,此题难度中等,容易漏掉隐含条件最简公分母不为0.
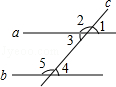
9.(3分)(2013•贵港)如图,直线a∥b,直线c与a、b都相交,从所标识的∠1、∠2、∠3、∠4、∠5这五个角中任意选取两个角,则所选取的两个角互为补角的概率是( )
A. 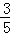 B.
B. 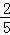 C.
C. 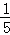 D.
D. 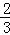
考点: 列表法与树状图法;平行线的性质
分析: 首先根据题意列出表格,然后由表格即可求得所有等可能的结果与所选取的两个角互为补角的情况,再利用概率公式求解即可求得答案.
解答: 解:列表得:
5 (1,5) (2,5) (3,5) (4,5) ﹣
4 (1,4) (2,4) (3,4) ﹣ (5,4)
3 (1,3) (2,3) ﹣ (4,3) (5,3)
2 (1,2) ﹣ (3,2) (4,2) (5,2)
1 ﹣ (2,1) (3,1) (4,1) (5,1)
1 2 3 4 5
∵共有20种等可能的结果,所选取的两个角互为补角的有12种情况,
∴所选取的两个角互为补角的概率是: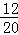 =
=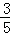 .
.
故选A.
点评: 本题考查的是用列表法或画树状图法求概率.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件,树状图法适合两步或两步以上完成的事件.注意概率=所求情况数与总情况数之比.
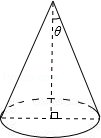
10.(3分)(2013•贵港)如图,已知圆锥的母线长为6,圆锥的高与母线所夹的角为θ,且sinθ=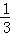 ,则该圆锥的侧面积是( )
,则该圆锥的侧面积是( )
A. 24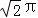 B. 24π C. 16π D. 12π
B. 24π C. 16π D. 12π
考点: 圆锥的计算.
专题: 计算题.
分析: 先根据正弦的定义计算出圆锥的半径=2,然后根据扇形的面积公式进行圆锥的侧面积.
解答: 解:∵sinθ=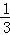 ,母线长为6,
,母线长为6,
∴圆锥的底面半径=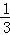 ×6=2,
×6=2,
∴该圆锥的侧面积=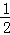 ×6×2π•2=12π.
×6×2π•2=12π.
故选D.
点评: 本题考查了圆锥的计算:圆锥的侧面展开图为扇形,扇形的弧长等于圆锥底面圆的周长,扇形的半径等于圆锥的母线长.
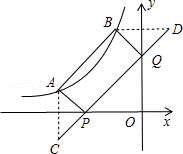
11.(3分)(2013•贵港)如图,点A(a,1)、B(﹣1,b)都在双曲线y=﹣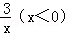 上,点P、Q分别是x轴、y轴上的动点,当四边形PABQ的周长取最小值时,PQ所在直线的解析式是( )
上,点P、Q分别是x轴、y轴上的动点,当四边形PABQ的周长取最小值时,PQ所在直线的解析式是( )
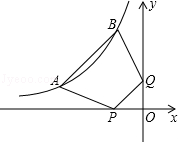
A. y=x B. y=x+1 C. y=x+2 D. y=x+3
考点: 反比例函数综合题.
专题: 综合题.
分析: 先把A点坐标和B点坐标代入反比例函数进行中可确定点A的坐标为(﹣3,1)、B点坐标为(﹣1,3),再作A点关于x轴的对称点C,B点关于y轴的对称点D,根据对称的性质得到C点坐标为(﹣3,﹣1),D点坐标为(1,3),CD分别交x轴、y轴于P点、Q点,根据两点之间线段最短得此时四边形PABQ的周长最小,然后利用待定系数法确定PQ的解析式.
解答: 解:分别把点A(a,1)、B(﹣1,b)代入双曲线y=﹣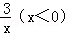 得a=﹣3,b=3,则点A的坐标为(﹣3,1)、B点坐标为(﹣1,3),
得a=﹣3,b=3,则点A的坐标为(﹣3,1)、B点坐标为(﹣1,3),
作A点关于x轴的对称点C,B点关于y轴的对称点D,所以C点坐标为(﹣3,﹣1),D点坐标为(1,3),
连结CD分别交x轴、y轴于P点、Q点,此时四边形PABQ的周长最小,
设直线CD的解析式为y=kx+b,
把C(﹣3,﹣1),D(1,3)分别代入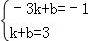 ,
,
解得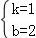 ,
,
所以直线CD的解析式为y=x+2.
故选C.
点评: 本题考查了反比例函数的综合题:掌握反比例函数图象上点的坐标特征、待定系数法求一次函数的解析式;熟练运用两点之间线段最短解决有关几何图形周长最短的问题.
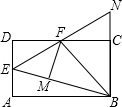
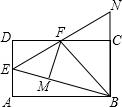
12.(3分)(2013•贵港)如图,在矩形ABCD中,点E是AD的中点,∠EBC的平分线交CD于点F,将△DEF沿EF折叠,点D恰好落在BE上M点处,延长BC、EF交于点N.有下列四个结论:①DF=CF;②BF⊥EN;③△BEN是等边三角形;④S△BEF=3S△DEF.其中,将正确结论的序号全部选对的是( )
A. ①②③ B. ①②④ C. ②③④ D. ①②③④
考点: 翻折变换(折叠问题);等边三角形的判定;矩形的性质
分析: 由折叠的性质、矩形的性质与角平分线的性质,可证得CF=FM=DF;
易求得∠BFE=∠BFN,则可得BF⊥EN;
易证得△BEN是等腰三角形,但无法判定是等边三角形;
易求得BM=2EM=2DE,即可得EB=3EM,根据等高三角形的面积比等于对应底的比,即可求得答案.
解答: 解:∵四边形ABCD是矩形,
∴∠D=∠BCD=90°,DF=MF,
由折叠的性质可得:∠EMF=∠D=90°,
即FM⊥BE,CF⊥BC,
∵BF平分∠EBC,
∴CF=MF,
∴DF=CF;故①正确;
∵∠BFM=90°﹣∠EBF,∠BFC=90°﹣∠CBF,
∴∠BFM=∠BFC,
∵∠MFE=∠DFE=∠CFN,
∴∠BFE=∠BFN,
∵∠BFE+∠BFN=180°,
∴∠BFE=90°,
即BF⊥EN,故②正确;
∵在△DEF和△CNF中,
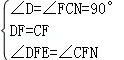 ,
,
∴△DEF≌△CNF(ASA),
∴EF=FN,
∴BE=BN,
但无法求得△BEN各角的度数,
∴△BEN不一定是等边三角形;故③错误;
∵∠BEM=∠BFC,BM⊥FM,BC⊥CF,
∴BM=BC=AD=2DE=2EM,
∴BM=3EM,
∴S△BEF=3S△EMF=3S△DEF;
故④正确.
故选B.
点评: 此题考查了折叠的性质、矩形的性质、角平分线的性质以及全等三角形的判定与性质.此题难度适中,注意掌握数形结合思想的应用.












