一、选择题:本题共12小题,在每小题所给出的四个选项中,只有一个是正确的.每小题4分,错选、不选或选出的答案超过一个,均记零分.
1.(4分)(2013•淄博)9的算术平方根是( )
A.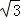 B.
B.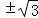 C. 3 D. ±3
C. 3 D. ±3
考点: 算术平方根.
分析: 根据算术平方根的定义求解即可.
解答: 解:∵32=9,
∴9的算术平方根是3.
故选C.
点评: 本题考查了算术平方根的定义,是基础题,熟记概念是解题的关键.
2.(4分)(2013•淄博)下列运算错误的是( )
A.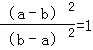 B.
B.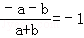
C.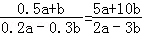 D.
D.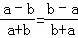
考点: 分式的基本性质.
分析: 根据分式的基本性质作答,分子分母同时扩大或缩小相同的倍数,分式的值不变,即可得出答案.
解答: 解:A、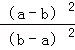 =
=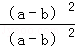 =1,故本选项正确;
=1,故本选项正确;
B、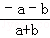 =
=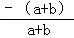 =﹣1,故本选项正确;
=﹣1,故本选项正确;
C、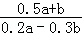 =
=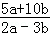 ,故本选项正确;
,故本选项正确;
D、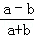 =﹣
=﹣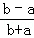 ,故本选项错误;
,故本选项错误;
故选D.
点评: 此题考查了分式的基本性质,无论是把分式的分子和分母扩大还是缩小相同的倍数,都不要漏乘(除)分子、分母中的任何一项,且扩大(缩小)的倍数不能为0.
3.(4分)(2013•淄博)把一根长100cm的木棍锯成两段,使其中一段的长比另一段的2倍少5cm,则锯出的木棍的长不可能为( )
A. 70cm B. 65cm C. 35cm D. 35cm或65cm
考点: 一元一次方程的应用.
分析: 设一段为x,则另一段为2x﹣5,再由总长为100cm,可得出方程,解出即可.
解答: 解:设一段为x,则另一段为2x﹣5,
由题意得,x+2x﹣5=100,
解得:x=35,2x﹣5=65.
故选A.
点评: 本题考查了一元一次方程的应用,解答本题的关键是设出未知数,根据总长为100cm得出方程,难度一般.
4.(4分)(2013•淄博)下面关于正六棱柱的视图(主视图、左视图、俯视图)中,画法错误的是( )
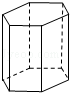
A. B.
B.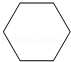 C.
C. D.
D.
考点: 简单组合体的三视图.
分析: 主视图,左视图,俯视图分别是从物体的正面,左面,上面看得到的图形.
解答: 解:从上面看易得俯视图为: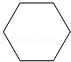 ,
,
从左面看易得左视图为: ,
,
从正面看主视图为: ,
,
故选A.
点评: 本题考查了几何体的三视图,解答本题的关键是掌握三视图的观察方向.
5.(4分)(2013•淄博)如果分式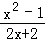 的值为0,则x的值是( )
的值为0,则x的值是( )
A. 1 B. 0 C. ﹣1 D. ±1
考点: 分式的值为零的条件.
分析: 根据分式的值为零的条件可以求出x的值.
解答: 解:由分式的值为零的条件得x2﹣1=0,2x+2≠0,
由x2﹣1=0,得x=±1,
由2x+2≠0,得x≠﹣1,
综上,得x=1.
故选A.
点评: 本题考查了分式的值为零的条件:(1)分子为0;(2)分母不为0.这两个条件缺一不可.
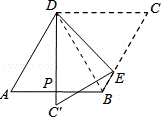
6.(4分)(2013•淄博)如图,菱形纸片ABCD中,∠A=60°,折叠菱形纸片ABCD,使点C落在DP(P为AB中点)所在的直线上,得到经过点D的折痕DE.则∠DEC的大小为( )
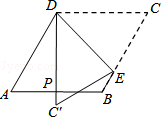
A. 78° B. 75° C. 60° D. 45°
考点: 翻折变换(折叠问题);菱形的性质.
专题: 计算题.
分析: 连接BD,由菱形的性质及∠A=60°,得到三角形ABD为等边三角形,P为AB的中点,利用三线合一得到DP为角平分线,得到∠ADP=30°,∠ADC=120°,∠C=60°,进而求出∠PDC=90°,由折叠的性质得到∠CDE=∠PDE=45°,利用三角形的内角和定理即可求出所求角的度数.
解答: 解:连接BD,
∵四边形ABCD为菱形,∠A=60°,
∴△ABD为等边三角形,∠ADC=120°,∠C=60°,
∵P为AB的中点,
∴DP为∠ADB的平分线,即∠ADP=∠BDP=30°,
∴∠PDC=90°,
∴由折叠的性质得到∠CDE=∠PDE=45°,
在△DEC中,∠DEC=180°﹣(∠CDE+∠C)=75°.
故选B.
点评: 此题考查了翻折变换(折叠问题),菱形的性质,等边三角形的性质,以及内角和定理,熟练掌握折叠的性质是解本题的关键.
7.(4分)(2013•淄博)如图,Rt△OAB的顶点A(﹣2,4)在抛物线y=ax2上,将Rt△OAB绕点O顺时针旋转90°,得到△OCD,边CD与该抛物线交于点P,则点P的坐标为( )
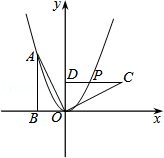
A. (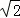 ,
,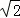 ) B. (2,2) C. (
) B. (2,2) C. (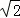 ,2) D. (2,
,2) D. (2,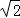 )
)
考点: 二次函数综合题.
专题: 综合题.
分析: 首先根据点A在抛物线y=ax2上求得抛物线的解析式和线段OB的长,从而求得点D的坐标,根据点P的纵坐标和点D的纵坐标相等得到点P的坐标即可;
解答: 解:∵Rt△OAB的顶点A(﹣2,4)在抛物线y=ax2上,
∴4=a×(﹣2)2,
解得:a=1
∴解析式为y=x2,
∵Rt△OAB的顶点A(﹣2,4),
∴OB=OD=2,
∵Rt△OAB绕点O顺时针旋转90°,得到△OCD,
∴CD∥x轴,
∴点D和点P的纵坐标均为2,
∴令y=2,得2=x2,
解得:x=±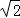 ,
,
∵点P在第一象限,
∴点P的坐标为:(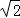 ,2)
,2)
故选:C.
点评: 本题考查了二次函数的综合知识,解题过程中首先求得直线的解析式,然后再求得点D的纵坐标,利用点P的纵坐标与点D的纵坐标相等代入函数的解析式求解即可.
8.(4分)(2013•淄博)如图,直角梯形ABCD中,AB∥CD,∠C=90°,∠BDA=90°,AB=a,BD=b,CD=c,BC=d,AD=e,则下列等式成立的是( )
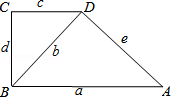
A. b2=ac B. b2=ce C. be=ac D. bd=ae
考点: 相似三角形的判定与性质;直角梯形.
分析: 根据∠CDB=∠DBA,∠C=∠BDA=90°,可判定△CDB∽△DBA,利用对应边成比例,即可判断各选项.
解答: 解:∵CD∥AB,
∴∠CDB=∠DBA,
又∵∠C=∠BDA=90°,
∴△CDB∽△DBA,
∴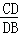 =
=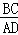 =
=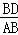 ,即
,即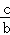 =
=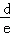 =
=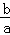 ,
,
A、b2=ac,成立,故本选项正确;
B、b2=ac,不是b2=ce,故本选项错误;
C、be=ad,不是be=ac,故本选项错误;
D、bd=ac,不是bd=ae,故本选项错误.
故选A.
点评: 本题考查了相似三角形的判定与性质,解答本题的关键是判断△CDB∽△DBA,注意掌握相似三角形的对应边成比例.
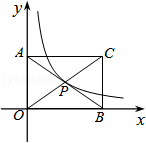
9.(4分)(2013•淄博)如图,矩形AOBC的面积为4,反比例函数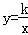 的图象的一支经过矩形对角线的交点P,则该反比例函数的解析式是( )
的图象的一支经过矩形对角线的交点P,则该反比例函数的解析式是( )
A.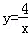 B.
B.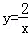 C.
C.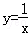 D.
D.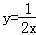
考点: 反比例函数系数k的几何意义.
专题: 计算题.
分析: 作PE⊥x轴,PF⊥y轴,根据矩形的性质得矩形OEPF的面积=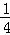 矩形AOBC的面积=
矩形AOBC的面积=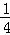 ×4=1,然后根据反比例函数y=
×4=1,然后根据反比例函数y=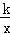 (k≠0)系数k的几何意义即可得到k=1.
(k≠0)系数k的几何意义即可得到k=1.
解答: 解:作PE⊥x轴,PF⊥y轴,如图,
∵点P为矩形AOBC对角线的交点,
∴矩形OEPF的面积=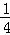 矩形AOBC的面积=
矩形AOBC的面积=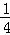 ×4=1,
×4=1,
∴|k|=1,
而k>0,
∴k=1,
∴过P点的反比例函数的解析式为y=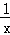 .
.
故选C.
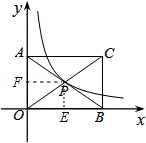
点评: 本题考查了反比例函数y=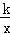 (k≠0)系数k的几何意义:从反比例函数y=
(k≠0)系数k的几何意义:从反比例函数y=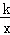 (k≠0)图象上任意一点向x轴和y轴作垂线,垂线与坐标轴所围成的矩形面积为|k|.
(k≠0)图象上任意一点向x轴和y轴作垂线,垂线与坐标轴所围成的矩形面积为|k|.
10.(4分)(2013•淄博)如果m是任意实数,则点P(m﹣4,m+1)一定不在( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
考点: 点的坐标.
分析: 求出点P的纵坐标一定大于横坐标,然后根据各象限的点的坐标特征解答.
解答: 解:∵(m+1)﹣(m﹣4)=m+1﹣m+4=5,
∴点P的纵坐标一定大于横坐标,
∵第四象限的点的横坐标是正数,纵坐标是负数,
∴第四象限的点的横坐标一定大于纵坐标,
∴点P一定不在第四象限.
故选D.
点评: 本题考查了点的坐标,记住各象限内点的坐标的符号是解决的关键,四个象限的符号特点分别是:第一象限(+,+);第二象限(﹣,+);第三象限(﹣,﹣);第四象限(+,﹣).
11.(4分)(2013•淄博)假定鸟卵孵化后,雏鸟为雌与雄的概率相同.如果三枚卵全部成功孵化,则三只雏鸟中恰有两只雌鸟的概率是( )
A.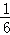 B.
B.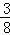 C.
C.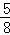 D.
D.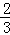
考点: 列表法与树状图法.
专题: 计算题.
分析: 画树状图得出所有等可能的情况数,找出恰有两只雌鸟的情况数,即可求出所求的概率.
解答: 解:画树状图,如图所示:
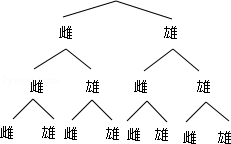
所有等可能的情况数有8种,其中三只雏鸟中恰有两只雌鸟的情况数有3种,
则P=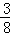 .
.
故选B.
点评: 此题考查了列表法与树状图法,用到的知识点为:概率=所求情况数与总情况数之比.












