评论
打印
一．选择题（本大题共8小题，每小题3分，满分24分。在每小题给出的四个选项中，只有一个是符合题目要求的，请将正确选项填在括号内。）
1．（2013宜宾）下列各数中，最小的数是（ ）
A．2 B．﹣3 C．﹣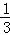
D．0
考点：有理数大小比较．
分析：根据正数都大于0，负数都小于0，正数大于一切负数，两个负数绝对值大的反而小，进行比较即可．
解答：解：∵﹣3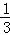＜﹣＜0＜2，
∴最小的数是﹣3；
故选B．
点评：此题考查了有理数的大小比较，要熟练掌握任意两个有理数比较大小的方法：正数都大于0，负数都小于0，正数大于一切负数，两个负数绝对值大的反而小．
2．（2013宜宾）据宜宾市旅游局公布的数据，今年“五一”小长假期间，全市实现旅游总收入330000000元．将330000000用科学记数法表示为（ ）
A．3.3×108 B．3.3×109 C．3.3×107 D．0.33×1010
考点：科学记数法—表示较大的数．
专题：计算题．
分析：找出所求数字的位数，减去1得到10的指数，表示成科学记数法即可．
解答：解：330000000用科学记数法表示为3.3×108．
故选A．
点评：此题考查了科学记数法﹣表示较大的数，科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．
3．（2013宜宾）下列水平放置的四个几何体中，主视图与其它三个不相同的是（ ）
A．
B．
C．
D．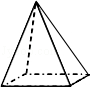
考点：简单几何体的三视图．
分析：分别找到四个几何体从正面看所得到的图形比较即可．
解答：解：A．主视图为长方形；
B．主视图为长方形；
C．主视图为长方形；
D．主视图为三角形．
则主视图与其它三个不相同的是D．
故选D．
点评：本题考查了三视图的知识，主视图是从物体的正面看得到的视图．
4．（2013宜宾）要判断小强同学的数学考试成绩是否稳定，那么需要知道他最近几次数学考试成绩的（ ）
A．方差 B．众数 C．平均数 D．中位数
考点：方差；统计量的选择．
分析：根据方差的意义作出判断即可．
解答：解：要判断小强同学的数学考试成绩是否稳定，只需要知道他最近几次数学考试成绩的方差即可．
故选A．
点评：本题考查方差的意义．方差是用来衡量一组数据波动大小的量，方差越大，表明这组数据偏离平均数越大，即波动越大，数据越不稳定；反之，方差越小，表明这组数据分布比较集中，各数据偏离平均数越小，即波动越小，数据越稳定．
5．（2013宜宾）若关于x的一元二次方程x2+2x+k=0有两个不相等的实数根，则k的取值范围是（ ）
A．k＜1 B．k＞1 C．k=1 D．k≥0
考点：根的判别式．
分析：判断上述方程的根的情况，只要看根的判别式△=b2﹣4ac的值的符号就可以了．
解答：解：∵关于x的一元二次方程x2+2x+k=0有两个不相等的实数根，a=1，b=2，c=k，
∴△=b2﹣4ac=22﹣4×1×k＞0，
∴k＜1，
故选：A．
点评：此题主要考查了根的判别式，一元二次方程根的情况与判别式△的关系：（1）△＞0⇔方程有两个不相等的实数根；（2）△=0⇔方程有两个相等的实数根；（3）△＜0⇔方程没有实数根．
6．（2013宜宾）矩形具有而菱形不具有的性质是（ ）
A．两组对边分别平行 B．对角线相等
C．对角线互相平分 D．两组对角分别相等
考点：矩形的性质；菱形的性质．
分析：根据矩形与菱形的性质对各选项分析判断后利用排除法求解．
解答：解：A．矩形与菱形的两组对边都分别平行，故本选项错误；
B．矩形的对角线相等，菱形的对角线不相等，故本选项正确；
C．矩形与菱形的对角线都互相平分，故本选项错误；
D．矩形与菱形的两组对角都分别相等，故本选项错误．
故选B．
点评：本题考查了矩形的性质，菱形的性质，熟记两图形的性质是解题的关键．
7．（2013宜宾）某棵果树前x年的总产量y与x之间的关系如图所示，从目前记录的结果看，前x年的年平均产量最高，则x的值为（ ）
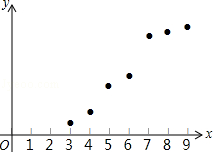
A．3 B．5 C．7 D．9
考点：算术平均数．
分析：由已知中图象表示某棵果树前x年的总产量y与n之间的关系，可分析出平均产量的几何意义为原点与该点边线的斜率，结合图象可得答案．
解答：解：若果树前x年的总产量y与n在图中对应P（x，y）点则前x年的年平均产量即为直线OP的斜率，
由图易得当x=7时，直线OP的斜率最大，
即前7年的年平均产量最高，x=7．
故选C．
点评：本题以函数的图象与图象变化为载体考查了斜率的几何意义，其中正确分析出平均产量的几何意义是解答本题的关键．
8．（2013宜宾）对于实数a、b，定义一种运算“⊗”为：a⊗b=a2+ab﹣2，有下列命题：①1⊗3=2；
②方程x⊗1=0的根为：x1=﹣2，x2=1；
③不等式组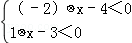
的解集为：﹣1＜x＜4；
④点（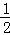
，
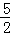）在函数y=x⊗（﹣1）的图象上．
其中正确的是（ ）
A．①②③④ B．①③ C．①②③ D．③④
考点：二次函数图象上点的坐标特征；有理数的混合运算；解一元二次方程-因式分解法；解一元一次不等式组；命题与定理．
专题：新定义．
分析：根据新定义得到1⊗3=12+1×3﹣2=2，则可对①进行判断；根据新定义由x⊗1=0得到x2+x﹣2=0，然后解方程可对②进行判断；根据新定义得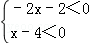
，解得﹣1＜x＜4，可对③进行判断；
根据新定义得y=x⊗（﹣1）=x2﹣x﹣2，然后把x=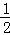代入计算得到对应的函数值，则可对④进行判断．
解答：解：1⊗3=12+1×3﹣2=2，所以①正确；
∵x⊗1=0，
∴x2+x﹣2=0，
∴x1=﹣2，x2=1，所以②正确；
∵（﹣2）⊗x﹣4=4﹣2x﹣2﹣4=﹣2x﹣2，1⊗x﹣3=1+x﹣2﹣3=x﹣4，
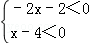∴，解得﹣1＜x＜4，所以③正确；
∵y=x⊗（﹣1）=x2﹣x﹣2，
∴当x=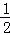
时，y=
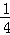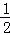﹣﹣2=﹣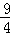
，所以④错误．
故选C．
点评：本题考查了二次函数图象上点的坐标特征：二次函数图象上点的坐标满足二次函数的解析式．也考查了阅读理解能力、解一元二次方程以及解一元一次不等式组．
二．填空题（本大题共8小题，每小题3分，满分24分。请把答案直接填在题中横线上。）
9．（2013宜宾）分式方程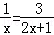
的解为 x=1 ．
考点：解分式方程．
专题：计算题．
分析：分式方程去分母转化为整式方程，求出整式方程的解得到x的值，经检验即可得到分式方程的解．
解答：解：去分母得：2x+1=3x，
解得：x=1，
经检验x=1是分式方程的解．
故答案为：x=1
点评：此题考查了解分式方程，解分式方程的基本思想是“转化思想”，把分式方程转化为整式方程求解．解分式方程一定注意要验根．
10．（2013宜宾）分解因式：am2﹣4an2= a（m+2n）（m﹣2n） ．
考点：提公因式法与公式法的综合运用．
分析：首先提取公因式a，再利用平方差公式进行二次分解即可．
解答：解：am2﹣4an2=a（m2﹣4n2）=a（m+2n）（m﹣2n），
故答案为：a（m+2n）（m﹣2n）．
点评：本题考查了用提公因式法和公式法进行因式分解，一个多项式有公因式首先提取公因式，然后再用其他方法进行因式分解，同时因式分解要彻底，直到不能分解为止．
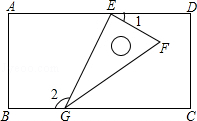
11．（2013宜宾）如图，一个含有30°角的直角三角形的两个顶点放在一个矩形的对边上，若∠1=25°，则∠2= 115° ．
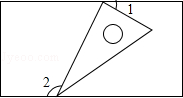
考点：平行线的性质．
分析：将各顶点标上字母，根据平行线的性质可得∠2=∠DEG=∠1+∠FEG，从而可得出答案．
解答：解：∵四边形ABCD是矩形，
∴AD∥BC，
∴∠2=∠DEG=∠1+∠FEG=115°．
故答案为：115°．
点评：本题考查了平行线的性质，解答本题的关键是掌握平行线的性质：两直线平行内错角相等．
