一.选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知集合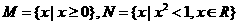 ,则
,则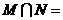 ( )
( )
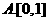
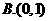
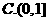
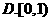
【答案】 D
【解析】
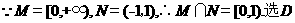
2.函数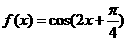 的最小正周期是( )
的最小正周期是( )
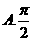
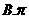
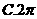
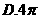
【答案】 B
【解析】
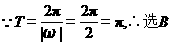
3.已知复数 Z = 2 - 1,则Z .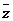 的值为( )
的值为( )
A.5 B.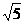 C.3 D.
C.3 D.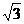
【答案】 A
【解析】
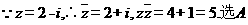
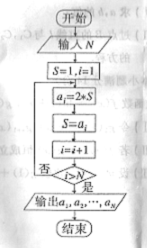
4.根据右边框图,对大于2的整数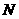 ,得出数列的通项公式是( )
,得出数列的通项公式是( )
 |
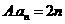
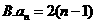
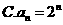
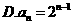
【答案】 C
【解析】

5.将边长为1的正方形以其一边所在的直线为旋转轴旋转一周,所得集合体的侧面积是( )
A.4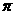 B.8
B.8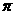 C.2
C.2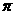 D.
D.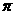
【答案】 C
【解析】
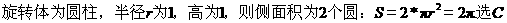
6.从正方形四个顶点及其中心这5个点中,任取2个点,则这2个点的距离不小于该正方形边长的概率为( )
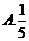
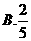
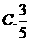
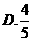
【答案】 B
【解析】

7.下列函数中,满足“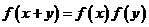 ”的单调递增函数是( )
”的单调递增函数是( )
(A)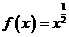 (B)
(B) (C)
(C)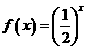 (D)
(D)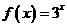
【答案】B
【解析】
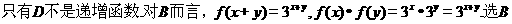
8.原命题为“若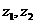 互为共轭复数,则
互为共轭复数,则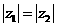 ”,关于逆命题,否命题,逆否命题真假性的判断依次如下,正确的是( )
”,关于逆命题,否命题,逆否命题真假性的判断依次如下,正确的是( )
(A)真,假,真 (B)假,假,真 (C)真,真,假 (D)假,假,假
【答案】A
【解析】

9.某公司10位员工的月工资(单位:元)为x1,x2,''',x10 ,其均值和方差分别为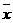 和s2,若从下月起每位员工的月工资增加100元,则这个10位员工下月工资的均值和方差分别为( )
和s2,若从下月起每位员工的月工资增加100元,则这个10位员工下月工资的均值和方差分别为( )
(A)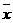 ,s2+1002 (B)
,s2+1002 (B)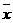 +100, s2+1002 (C)
+100, s2+1002 (C) 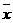 ,s2 (D)
,s2 (D)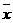 +100, s2
+100, s2
【答案】 D
【解析】

10.如图,修建一条公路需要一段环湖弯曲路段与两条直道为某三次函数图像的一部分,则该函数的解析式为( )
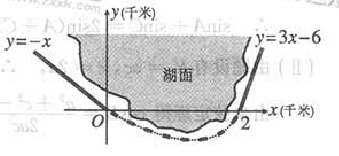
(A)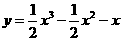 (B)
(B)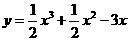
(C)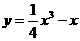 (D)
(D)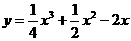
【答案】 A
【解析】
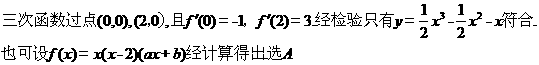
二、填空题:把答案填写在答题卡相应题号后的横线上(本大题共5小题,每小题5分,共25分).
抛物线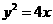 的准线方程为___________.
的准线方程为___________.
【答案】 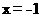
【解析】
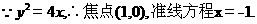
已知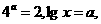 则
则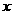 =________.
=________.
【答案】 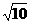
【解析】
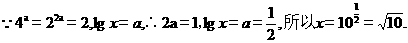
13. 设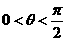 ,向量
,向量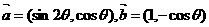 ,若
,若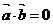 ,则
,则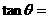 ______.
______.
【答案】 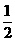
【解析】
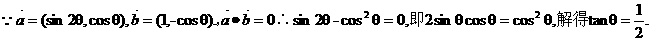
已知f(x)=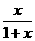 ,x≥0, f1(x)=f(x),fn+1(x)=f(fn(x)),n
,x≥0, f1(x)=f(x),fn+1(x)=f(fn(x)),n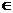 N+, 则f2014(x)的表达式为__________.
N+, 则f2014(x)的表达式为__________.
【答案】 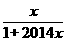
【解析】
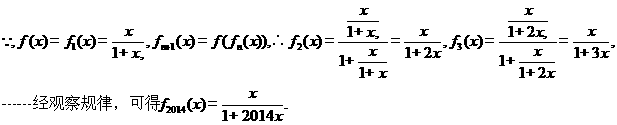
15.(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)
 (不等式选做题)设
(不等式选做题)设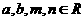 ,且
,且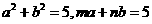 ,则
,则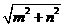 的最小值为
的最小值为
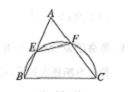
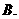 (几何证明选做题)如图,
(几何证明选做题)如图,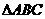 中,
中,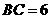 ,以
,以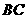 为直径的半圆分别交
为直径的半圆分别交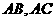 于点
于点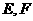 ,若
,若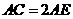 ,则
,则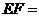
 (坐标系与参数方程选做题)在极坐标系中,点
(坐标系与参数方程选做题)在极坐标系中,点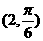 到直线
到直线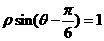 的距离是
的距离是
【答案】 A 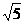 B 3 C 1
B 3 C 1
【解析】
A
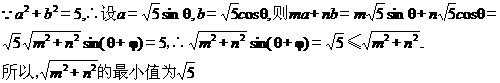
B
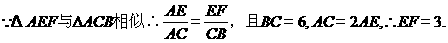
C













