2014年高考数学真题附答案和解析Word版(理科+陕西卷)
一.选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知集合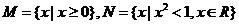 ,则
,则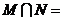 ( )
( )
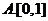
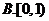
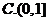
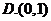
【答案】 B
【解析】
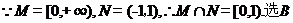
2.函数 的最小正周期是( )
的最小正周期是( )
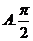
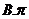
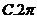
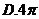
【答案】 B
【解析】
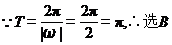
3.定积分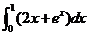 的值为( )
的值为( )
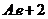
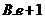
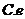
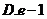
【答案】 C
【解析】
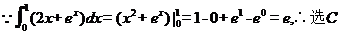
4.根据右边框图,对大于2的整数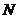 ,输出数列的通项公式是( )
,输出数列的通项公式是( )
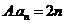
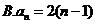
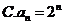
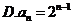
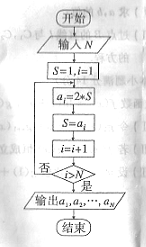
【答案】 C
【解析】
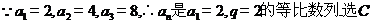
5.已知底面边长为1,侧棱长为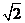 则正四棱柱的各顶点均在同一个球面上,则该球的体积为( )
则正四棱柱的各顶点均在同一个球面上,则该球的体积为( )
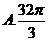
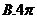
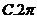
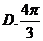
【答案】 D
【解析】
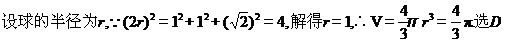
6.从正方形四个顶点及其中心这5个点中,任取2个点,则这2个点的距离不小于该正方形边长的概率为( )
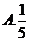
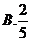
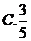
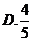
【答案】 C
【解析】
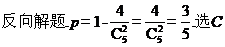
下列函数中,满足“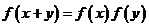 ”的单调递增函数是( ) (A)
”的单调递增函数是( ) (A)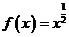 (B)
(B)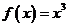 (C)
(C)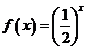 (D)
(D)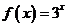
【答案】 D
【解析】
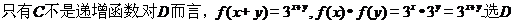
8.原命题为“若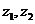 互为共轭复数,则
互为共轭复数,则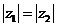 ”,关于逆命题,否命题,逆否命题真假性的判断依次如下,正确的是( )
”,关于逆命题,否命题,逆否命题真假性的判断依次如下,正确的是( )
(A)真,假,真 (B)假,假,真 (C)真,真,假 (D)假,假,假
【答案】 B
【解析】
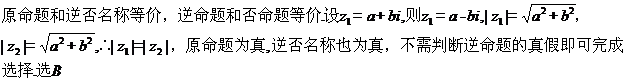
设样本数据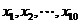 的均值和方差分别为1和4,若
的均值和方差分别为1和4,若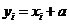 (
(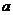 为非零常数,
为非零常数, 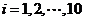 ),则
),则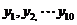 的均值和方差分别为( )
的均值和方差分别为( )
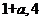 (B)
(B)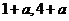 (C)
(C)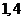 (D)
(D)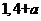
【答案】 A
【解析】
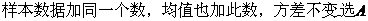
10.如图,某飞行器在4千米高空水平飞行,从距着陆点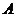 的水平距离10千米处下降, 已知下降飞行轨迹为某三次函数图像的一部分,则函数的解析式为( )
的水平距离10千米处下降, 已知下降飞行轨迹为某三次函数图像的一部分,则函数的解析式为( )
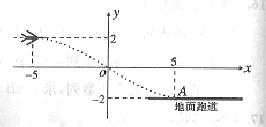
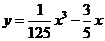 (B)
(B)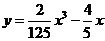
(C)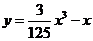 (D)
(D)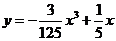
【答案】 A
【解析】
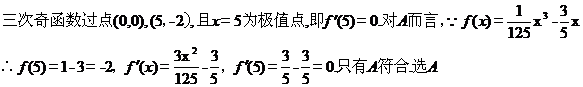 第二部分(共100分)
第二部分(共100分)
填空题:把答案填写在答题卡相应题号后的横线上(本大题共5小题,每小题5分,共25分).
已知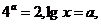 则
则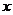 =________.
=________.
【答案】 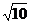
【解析】
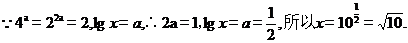
若圆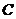 的半径为1,其圆心与点
的半径为1,其圆心与点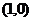 关于直线
关于直线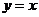 对称,则圆
对称,则圆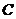 的标准方程为_______.
的标准方程为_______.
【答案】 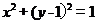
【解析】
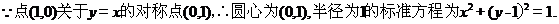
设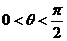 ,向量
,向量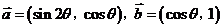 ,若
,若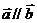 ,则
,则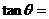 _______.
_______.
【答案】 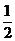
【解析】 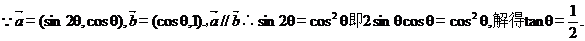
14. 观察分析下表中的数据:
多面体 | 面数( | 顶点数( | 棱数( |
三棱锥 | 5 | 6 | 9 |
五棱锥 | 6 | 6 | 10 |
立方体 | 6 | 8 | 12 |
猜想一般凸多面体中,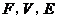 所满足的等式是_________.
所满足的等式是_________.
【答案】 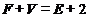
【解析】
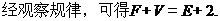
15.(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)
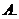 (不等式选做题)设
(不等式选做题)设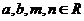 ,且
,且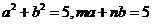 ,则
,则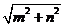 的最小值为
的最小值为
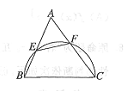
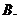 (几何证明选做题)如图,
(几何证明选做题)如图,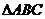 中,
中,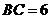 ,以
,以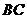 为直径的半圆分别交
为直径的半圆分别交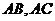 于点
于点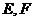 ,若
,若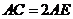 ,则
,则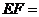
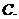 (坐标系与参数方程选做题)在极坐标系中,点
(坐标系与参数方程选做题)在极坐标系中,点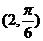 到直线
到直线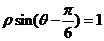 的距离是
的距离是
【答案】 A 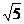 B 3 C 1
B 3 C 1
【解析】
A
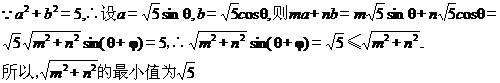
B
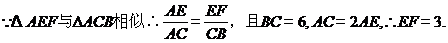
C
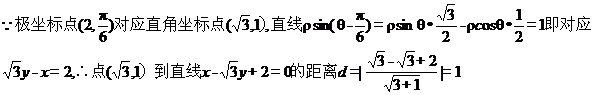
三、解答题:解答应写出文字说明、证明过程或演算步骤(本大题共6小题,共75分)
16. (本小题满分12分)
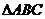 的内角
的内角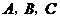 所对的边分别为
所对的边分别为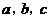 .
.
(I)若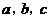 成等差数列,证明:
成等差数列,证明: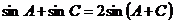 ;
;
(II)若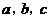 成等比数列,求
成等比数列,求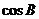 的最小值.
的最小值.
【答案】 (1) 省略 (2) 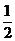
【解析】
(1)
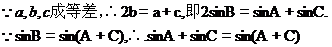
(2)
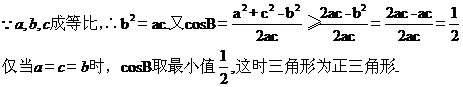
(本小题满分12分)
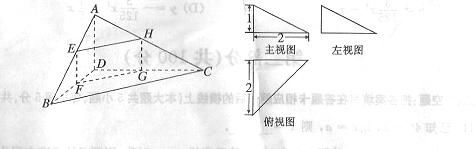
四面体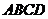 及其三视图如图所示,过棱
及其三视图如图所示,过棱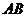 的中点
的中点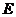 作平行于
作平行于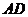 ,
,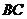 的平面分
的平面分
别交四面体的棱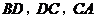 于点
于点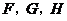 .
.
(I)证明:四边形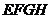 是矩形;
是矩形;
(II)求直线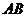 与平面
与平面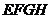 夹角
夹角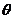 的正弦值.
的正弦值.
【答案】 (1) 省略 (2) 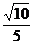
【解析】
(1)

(2)
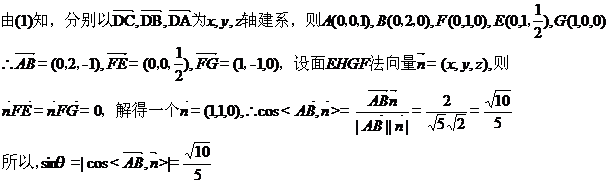
18.(本小题满分12分)
在直角坐标系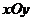 中,已知点
中,已知点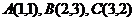 ,点
,点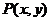 在
在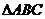 三边围成的
三边围成的
区域(含边界)上
(1)若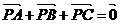 ,求
,求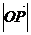 ;
;
(2)设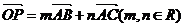 ,用
,用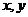 表示
表示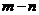 ,并求
,并求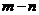 的最大值.【答案】 (1)
的最大值.【答案】 (1) 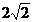 (2) m-n=y-x, 1
(2) m-n=y-x, 1
【解析】
(1)
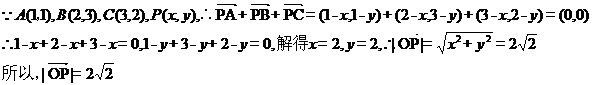 (2)
(2)
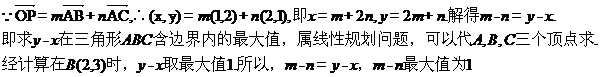
19.(本小题满分12分)
在一块耕地上种植一种作物,每季种植成本为1000元,此作物的市场价格和这块地上
的产量具有随机性,且互不影响,其具体情况如下表:

(1)设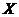 表示在这块地上种植1季此作物的利润,求
表示在这块地上种植1季此作物的利润,求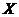 的分布列;
的分布列;
(2)若在这块地上连续3季种植此作物,求这3季中至少有2季的利润不少于2000元
的概率.
【答案】 (1)(800,0.2)(2000,0.5)(4000,0.3) (2) 0.896
【解析】
(1)
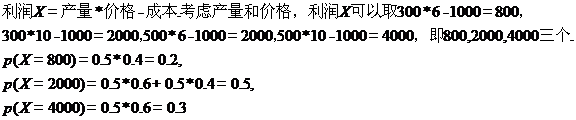
X的分布列如下表:
X | 800 | 2000 | 4000 |
P | 0.2 | 0.5 | 0.3 |
(2)
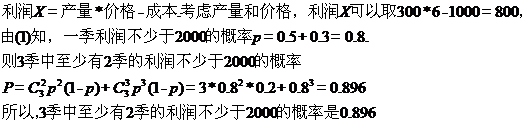
(本小题满分13分)
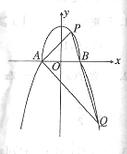
如图,曲线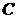 由上半椭圆
由上半椭圆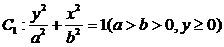 和部分抛物线
和部分抛物线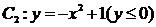 连接而成,
连接而成,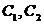 的公共点为
的公共点为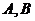 ,其中
,其中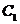 的离心率为
的离心率为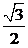 .
.
求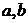 的值;
的值;
过点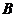 的直线
的直线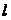 与
与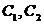 分别交于
分别交于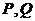 (均异于点
(均异于点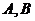 ),若
),若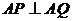 ,求直线
,求直线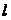 的方程.
的方程.
【答案】 (1) a=2,b=1 (2) 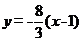
【解析】
(1)
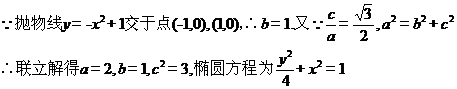
(2)
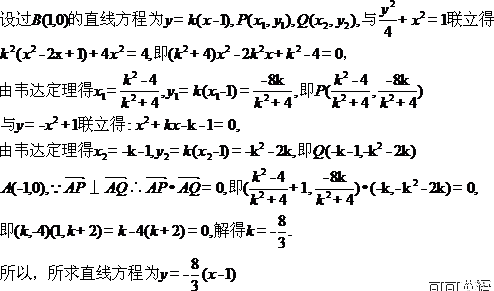
21.(本小题满分14分)
设函数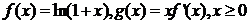 ,其中
,其中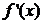 是
是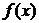 的导函数.
的导函数.
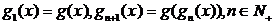 ,求
,求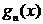 的表达式;
的表达式;
若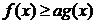 恒成立,求实数
恒成立,求实数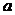 的取值范围;
的取值范围;
(3)设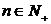 ,比较
,比较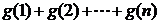 与
与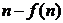 的大小,并加以证明.
的大小,并加以证明.
【答案】 (1) 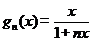 (2)
(2) 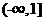 (3) 前式 > 后式
(3) 前式 > 后式
【解析】
(1)
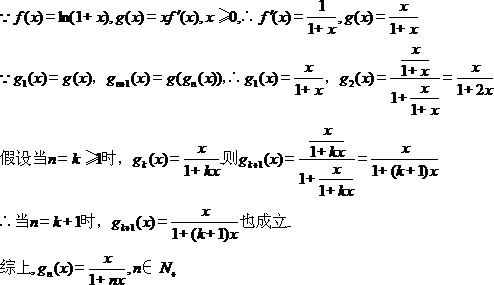
(2)
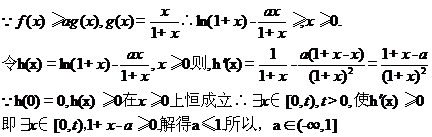
(3)
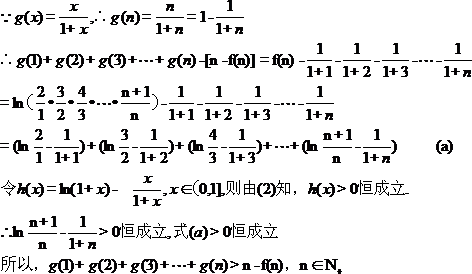



 )
) )
) )
)








