第Ⅰ卷共10小题。
一、选择题:本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一个是符合题目要求的。
1、已知集合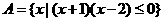 ,集合
,集合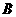 为整数集,则
为整数集,则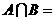 ( )
( )
A、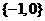 B、
B、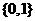 C、
C、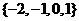 D、
D、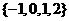
【答案】D
【解析】
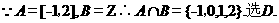
2、在“世界读书日”前夕,为了了解某地 名居民某天的阅读时间,从中抽取了
名居民某天的阅读时间,从中抽取了 名居民的阅读时间进行统计分析。在这个问题中,
名居民的阅读时间进行统计分析。在这个问题中, 名居民的阅读时间的全体是( )
名居民的阅读时间的全体是( )
A、总体 B、个体
C、样本的容量 D、从总体中抽取的一个样本
【答案】A
【解析】

3、为了得到函数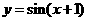 的图象,只需把函数
的图象,只需把函数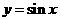 的图象上所有的点( )
的图象上所有的点( )
A、向左平行移动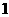 个单位长度 B、向右平行移动
个单位长度 B、向右平行移动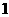 个单位长度
个单位长度
C、向左平行移动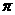 个单位长度 D、向右平行移动
个单位长度 D、向右平行移动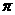 个单位长度
个单位长度
【答案】A
【解析】
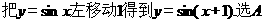
4、某三棱锥的侧视图、俯视图如图所示,则该三棱锥的体积是( )(锥体体积公式: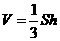 ,其中
,其中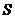 为底面面积,
为底面面积,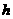 为高)
为高)
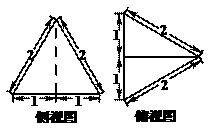
A、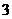 B、
B、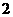 C、
C、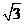 D、
D、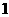
【答案】D
【解析】
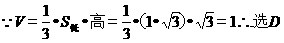
5、若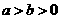 ,
,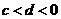 ,则一定有( )
,则一定有( )
A、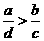 B、
B、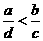
C、 D、
D、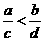
【答案】B
【解析】
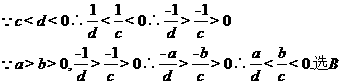
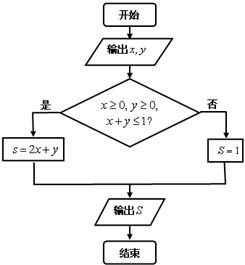
6、执行如图的程序框图,如果输入的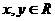 ,那么输出的
,那么输出的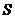 的最大值为( )
的最大值为( )
A、 B、
B、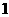 C、
C、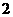 D、
D、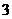
【答案】C
【解析】
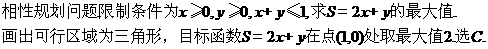
7、已知 ,
,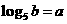 ,
,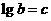 ,
,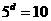 ,则下列等式一定成立的是( )
,则下列等式一定成立的是( )
A、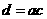 B、
B、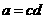 C、
C、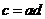 D、
D、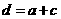
【答案】B
【解析】
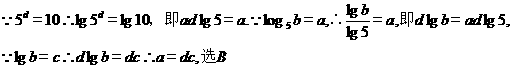
8、如图,从气球 上测得正前方的河流的两岸
上测得正前方的河流的两岸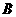 ,
,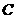 的俯角分别为
的俯角分别为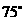 ,
, ,此时气球的高是
,此时气球的高是 ,则河流的宽度
,则河流的宽度 等于( )
等于( )

A、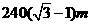 B、
B、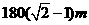
C、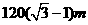 D、
D、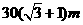
【答案】C
【解析】
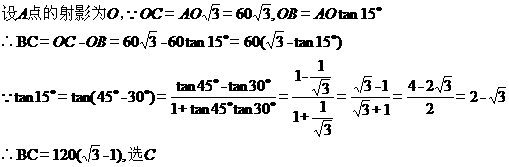
9、设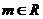 ,过定点
,过定点 的动直线
的动直线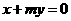 和过定点
和过定点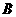 的动直线
的动直线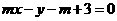 交于点
交于点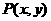 ,则
,则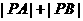 的取值范围是( )
的取值范围是( )
A、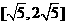 B、
B、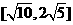 C、
C、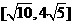 D、
D、
【答案】B
【解析】
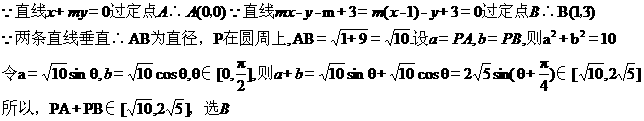
10、已知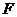 为抛物线
为抛物线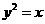 的焦点,点
的焦点,点 ,
,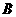 在该抛物线上且位于
在该抛物线上且位于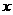 轴的两侧,
轴的两侧,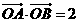 (其中
(其中 为坐标原点),则
为坐标原点),则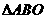 与
与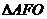 面积之和的最小值是( )
面积之和的最小值是( )
A、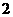 B、
B、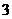 C、
C、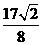 D、
D、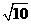
【答案】B
【解析】
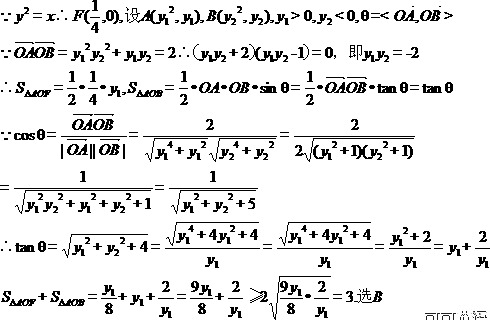
第Ⅱ卷 (非选择题 共100分)第Ⅱ卷共11小题。
二、填空题:本大题共5小题,每小题5分,共25分。
11、双曲线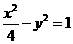 的离心率等于____________。
的离心率等于____________。
【答案】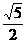
【解析】
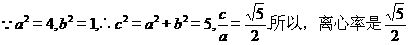
12、复数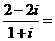 ____________。
____________。
【答案】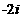
【解析】
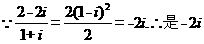
13、设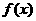 是定义在
是定义在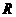 上的周期为
上的周期为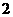 的函数,当
的函数,当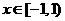 时,
时,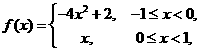 ,则
,则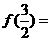 ____________。
____________。
【答案】1
【解析】
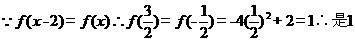
14、平面向量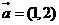 ,
,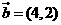 ,
,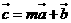 (
(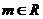 ),且
),且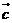 与
与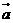 的夹角等于
的夹角等于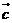 与
与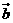 的夹角,则
的夹角,则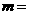 ____________。
____________。
【答案】2
【解析】
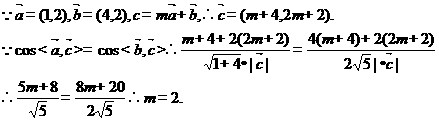
15、以 表示值域为
表示值域为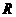 的函数组成的集合,
的函数组成的集合,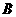 表示具有如下性质的函数
表示具有如下性质的函数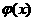 组成的集合:对于函数
组成的集合:对于函数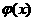 ,存在一个正数
,存在一个正数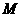 ,使得函数
,使得函数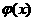 的值域包含于区间
的值域包含于区间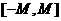 。例如,当
。例如,当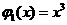 ,
,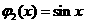 时,
时,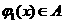 ,
,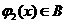 。现有如下命题:
。现有如下命题:
①设函数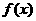 的定义域为
的定义域为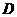 ,则“
,则“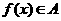 ”的充要条件是“
”的充要条件是“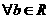 ,
,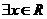 ,
,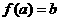 ”;
”;
②若函数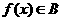 ,则
,则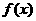 有最大值和最小值;
有最大值和最小值;
③若函数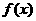 ,
,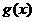 的定义域相同,且
的定义域相同,且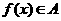 ,
,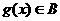 ,则
,则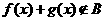 ;
;
④若函数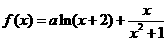 (
(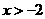 ,
,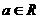 )有最大值,则
)有最大值,则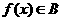 。
。
其中的真命题有____________。(写出所有真命题的序号)。
【答案】 (1)(3) (4)
【解析】

三、解答题:本大题共6小题,共75分。解答应写出文字说明,证明过程或演算步骤。
16、(本小题满分12分)
一个盒子里装有三张卡片,分别标记有数字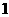 ,
,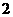 ,
,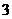 ,这三张卡片除标记的数字外完全相同。随机有放回地抽取
,这三张卡片除标记的数字外完全相同。随机有放回地抽取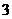 次,每次抽取
次,每次抽取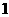 张,将抽取的卡片上的数字依次记为
张,将抽取的卡片上的数字依次记为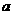 ,
,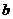 ,
,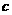 。
。
(Ⅰ)求“抽取的卡片上的数字满足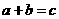 ”的概率;
”的概率;
(Ⅱ)求“抽取的卡片上的数字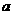 ,
,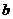 ,
,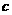 不完全相同”的概率。
不完全相同”的概率。
【答案】 (Ⅰ)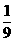 (Ⅱ)
(Ⅱ)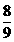
【解析】
(Ⅰ)

(Ⅲ)

17、(本小题满分12分)
已知函数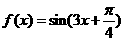
(Ⅰ)求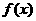 的单调递增区间;
的单调递增区间;
(Ⅱ)若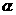 是第二象限角,
是第二象限角,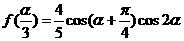 ,求
,求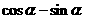 的值。
的值。
【答案】 (Ⅰ)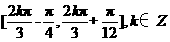 (Ⅱ)
(Ⅱ)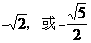
【解析】
(Ⅰ)
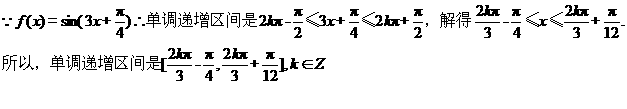 (Ⅱ)
(Ⅱ)
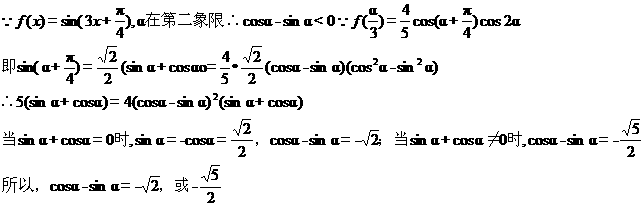
18、(本小题满分12分)
在如图所示的多面体中,四边形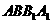 和
和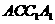 都为矩形。
都为矩形。

(Ⅰ)若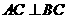 ,证明:直线
,证明:直线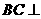 平面
平面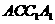 ;
;
(Ⅱ)设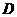 ,
,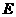 分别是线段
分别是线段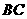 ,
,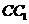 的中点,在线段
的中点,在线段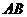 上是否存在一点
上是否存在一点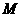 ,使直线
,使直线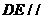 平面
平面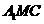 ?请证明你的结论。
?请证明你的结论。
【答案】 (Ⅰ)省略 (Ⅱ) 存在,点M为AB中点
【解析】
(Ⅰ)
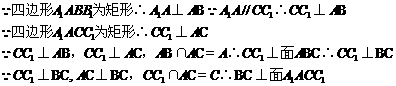
(Ⅱ)

19、(本小题满分12分)
设等差数列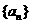 的公差为
的公差为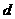 ,点
,点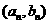 在函数
在函数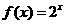 的图象上(
的图象上(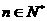 )。
)。
(Ⅰ)证明:数列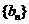 为等差数列;
为等差数列;
(Ⅱ)若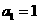 ,函数
,函数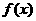 的图象在点
的图象在点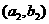 处的切线在
处的切线在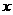 轴上的截距为
轴上的截距为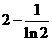 ,求数列
,求数列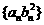 的前
的前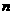 项和
项和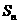 。
。
【答案】 (Ⅰ) (Ⅱ) 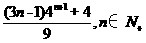
【解析】
(Ⅰ)
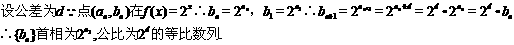
(Ⅱ)

20、(本小题满分13分)
已知椭圆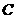 :
: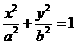 (
(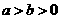 )的左焦点为
)的左焦点为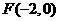 ,离心率为
,离心率为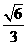 。
。
(Ⅰ)求椭圆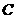 的标准方程;
的标准方程;
(Ⅱ)设 为坐标原点,
为坐标原点,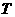 为直线
为直线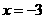 上一点,过
上一点,过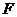 作
作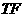 的垂线交椭圆于
的垂线交椭圆于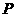 ,
,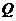 。当四边形
。当四边形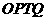 是平行四边形时,求四边形
是平行四边形时,求四边形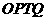 的面积。
的面积。
【答案】 (Ⅰ)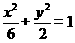 (Ⅱ)
(Ⅱ) 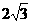
【解析】
(Ⅰ)
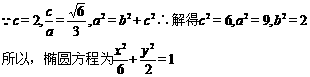
(Ⅱ-1)

21、(本小题满分14分)
已知函数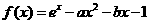 ,其中
,其中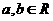 ,
,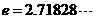 为自然对数的底数。
为自然对数的底数。
(Ⅰ)设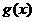 是函数
是函数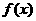 的导函数,求函数
的导函数,求函数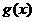 在区间
在区间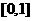 上的最小值;
上的最小值;
(Ⅱ)若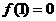 ,函数
,函数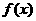 在区间
在区间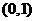 内有零点,证明:
内有零点,证明: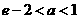 。
。
【答案】
(Ⅰ) 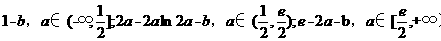
(Ⅱ) 省略
【解析】
(Ⅰ)

(Ⅱ)

















