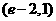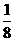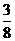一.选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一个是符合题目要求的。
1.已知集合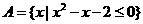 ,集合
,集合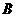 为整数集,则
为整数集,则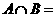
A.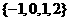 B.
B.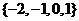 C.
C.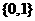 D.
D.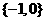
【答案】A
【解析】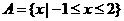 ,
,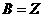 ,故
,故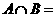
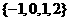
2.在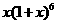 的展开式中,含
的展开式中,含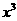 项的系数为
项的系数为
A. B.
B.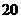 C.
C.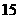 D.
D.
【答案】C
【解析】含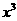 项为
项为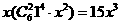
3.为了得到函数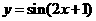 的图象,只需把函数
的图象,只需把函数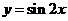 的图象上
的图象上
所有的点
A.向左平行移动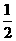 个单位长度 B.向右平行移动
个单位长度 B.向右平行移动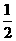 个单位长度
个单位长度
C.向左平行移动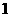 个单位长度 D.向右平行移动
个单位长度 D.向右平行移动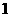 个单位长度
个单位长度
【答案】A
【解析】因为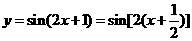 ,故可由函数
,故可由函数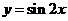 的图象上所有的点向左平行移动
的图象上所有的点向左平行移动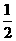 个单位长度得到
个单位长度得到
4.若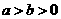 ,
,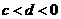 ,则一定有
,则一定有
A.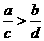 B.
B.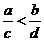 C.
C.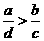 D.
D.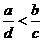
【答案】D
【解析】由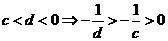 ,又
,又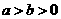 ,由不等式性质知:
,由不等式性质知: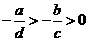 ,所以
,所以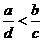
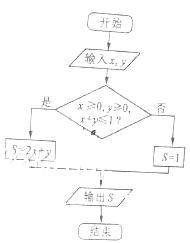
5.执行如图1所示的程序框图,如果输入的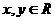 ,则输出的
,则输出的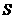 的最大值为
的最大值为
A. B.
B.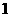 C.
C.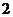 D.
D.
【答案】C
【解析】当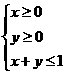 时,函数
时,函数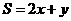 的最大值为2,否则,
的最大值为2,否则,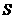 的值为1.
的值为1.
6.六个人从左至右排成一行,最左端只能排甲或乙,最右端不能拍甲,则不同的排法共有
A.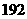 种 B.
种 B.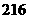 种 C.
种 C.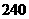 种 D.
种 D.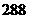 种
种
【答案】B
【解析】当最左端为甲时,不同的排法共有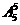 种;当最左端为乙时,不同的排法共有
种;当最左端为乙时,不同的排法共有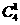
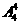 种。
种。
共有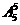 +
+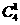
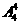
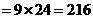 种
种
7.平面向量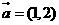 ,
,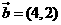 ,
,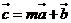 (
(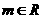 ),且
),且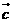 与
与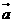 的夹角等于
的夹角等于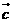 与
与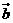 的夹角,则
的夹角,则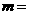
A.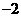 B.
B.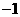 C.
C.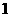 D.
D.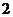
【答案】D
【解析1】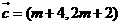
因为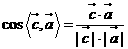 ,
,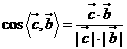 ,所以
,所以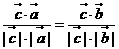 ,又
,又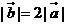
所以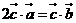 即
即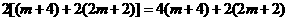
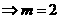
【解析2】由几何意义知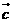 为以
为以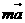 ,
,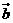 为邻边的菱形的对角线向量,又
为邻边的菱形的对角线向量,又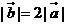 故
故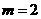
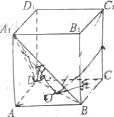
8.如图,在正方体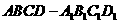 中,点
中,点 为线段
为线段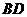 的中点。设点
的中点。设点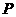 在线段
在线段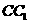 上,直线
上,直线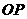 与平面
与平面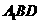 所成的角为
所成的角为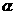 ,则
,则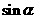 的取值范围是
的取值范围是
A.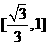 B.
B.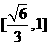 C.
C.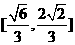 D.
D.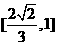
【答案】B
【解析】直线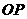 与平面
与平面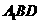 所成的角为
所成的角为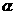 的取值范围是
的取值范围是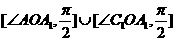 ,
,
由于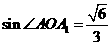 ,
,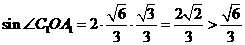 ,
,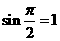 所以
所以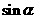 的取值范围是
的取值范围是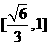
9.已知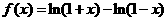 ,
,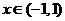 。现有下列命题:
。现有下列命题:
①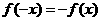 ;②
;②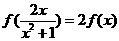 ;③
;③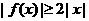 。其中的所有正确命题的序号是
。其中的所有正确命题的序号是
A.①②③ B.②③ C.①③ D.①②
【答案】C
【解析】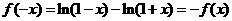 故①正确
故①正确
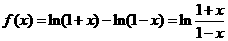
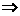
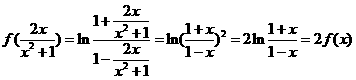
但左边的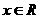 ,右边的
,右边的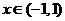 ,故②不正确
,故②不正确
当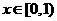 时,
时,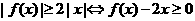
令 (
(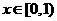 )
)
因为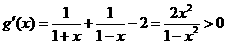 ,所以
,所以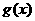 在
在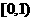 单增,
单增,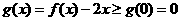
即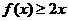 ,又
,又 与
与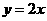 为奇函数,所以
为奇函数,所以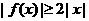 成立故③正确
成立故③正确
10.已知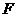 是抛物线
是抛物线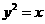 的焦点,点
的焦点,点 ,
,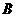 在该抛物线上且位于
在该抛物线上且位于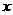 轴的两侧,
轴的两侧,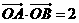 (其中
(其中 为
为
坐标原点),则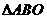 与
与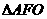 面积之和的最小值是
面积之和的最小值是
A.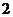 B.
B.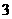 C.
C.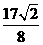 D.
D.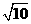
【答案】B
【解析】设直线AB的方程为: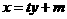 ,点
,点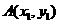 ,
,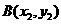 ,又
,又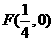 ,直线AB与
,直线AB与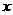 轴的交点
轴的交点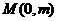 (不妨假设
(不妨假设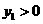 )
)
 由
由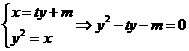 ,所以
,所以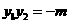
又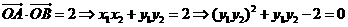
因为点 ,
,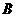 在该抛物线上且位于
在该抛物线上且位于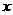 轴的两侧,所以
轴的两侧,所以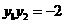 ,故
,故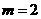
于是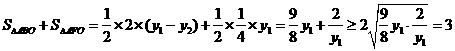
当且仅当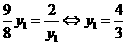 时取“
时取“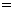 ”
”
所以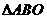 与
与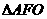 面积之和的最小值是
面积之和的最小值是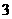
二.填空题:本大题共5小题,每小题5分,共25分。
11.复数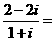 _____________。
_____________。
【答案】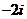
【解析】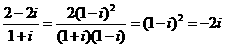
12.设 是定义在R上的周期为2的函数,当
是定义在R上的周期为2的函数,当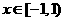 时,
时,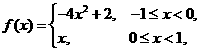 ,则
,则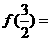 ___________。
___________。
【答案】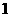
【解析】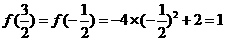
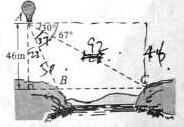
13.如图,从气球A上测得正前方的河流的两岸B,C的俯角分别为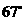 ,
, ,此时气球的高是
,此时气球的高是 ,则河流的宽度BC约等于___________
,则河流的宽度BC约等于___________  。(用四舍五入法将结果精确到个位。参考数据:
。(用四舍五入法将结果精确到个位。参考数据: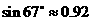 ,
,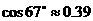 ,
,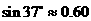 ,
,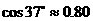 ,
,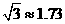 )
)
【答案】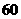
【解析】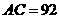 ,
,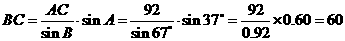
14.设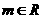 ,过定点A的动直线
,过定点A的动直线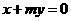 和过定点B的动直线
和过定点B的动直线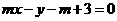 交于点
交于点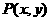 ,则
,则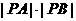 的最大值是___________。
的最大值是___________。
【答案】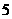
【解析】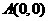 ,
,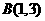 ,因为
,因为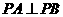 ,所以
,所以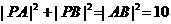 ,故
,故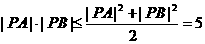 (当且仅当
(当且仅当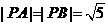 时取“
时取“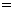 ”)
”)
15.以 表示值域为R的函数组成的集合,
表示值域为R的函数组成的集合,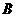 表示具有如下性质的函数
表示具有如下性质的函数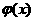 组成的集合:对于函数
组成的集合:对于函数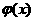 ,存在一个正数
,存在一个正数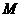 ,使得函数
,使得函数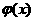 的值域包含于区间
的值域包含于区间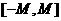 。例如,当
。例如,当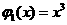 ,
,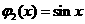 时,
时,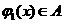 ,
,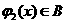 。现有如下命题:
。现有如下命题:
①设函数 的定义域为
的定义域为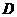 ,则“
,则“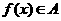 ”的充要条件是“
”的充要条件是“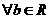 ,
,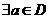 ,
, ”;
”;
②函数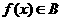 的充要条件是
的充要条件是 有最大值和最小值;
有最大值和最小值;
③若函数 ,
,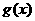 的定义域相同,且
的定义域相同,且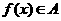 ,
,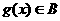 ,则
,则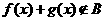 ;
;
④若函数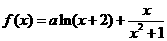 (
(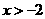 ,
,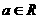 )有最大值,则
)有最大值,则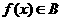 。
。
其中的真命题有___________ 。(写出所有真命题的序号)
【答案】①③④
三.解答题:本大题共6小题,共 75分。解答须写出文字说明,证明过程或演算步骤。
16.已知函数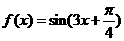 。
。
(1)求 的单调递增区间;
的单调递增区间;
(2)若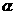 是第二象限角,
是第二象限角,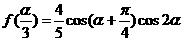 ,求
,求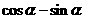 的值。
的值。
解:(1)由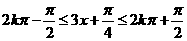
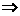
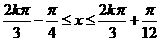
所以 的单调递增区间为
的单调递增区间为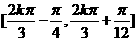 (
(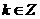 )
)
(2)由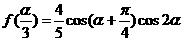
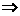
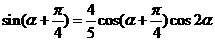
因为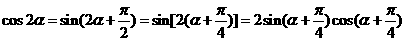
所以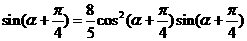
又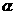 是第二象限角,所以
是第二象限角,所以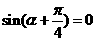 或
或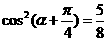
①由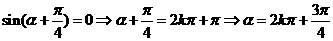 (
(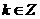 )
)
所以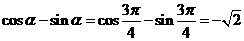
②由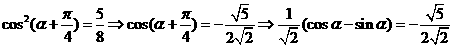
所以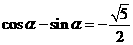
综上,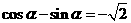 或
或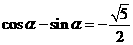
17.一款击鼓小游戏的规则如下:每盘游戏都需要击鼓三次,每次击鼓要么出现一次音乐,要么不出现音乐;每盘游戏击鼓三次后,出现一次音乐获得10分,出现两次音乐获得20分,出现三次音乐获得100分,没有出现音乐则扣除200分(即获得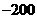 分)。设每次击鼓出现音乐的概率为
分)。设每次击鼓出现音乐的概率为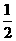 ,且各次击鼓出现音乐相互独立。
,且各次击鼓出现音乐相互独立。
(1)设每盘游戏获得的分数为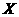 ,求
,求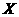 的分布列;
的分布列;
(2)玩三盘游戏,至少有一盘出现音乐的概率是多少?
(3)玩过这款游戏的许多人都发现,若干盘游戏后,与最初的分数相比,分数没有增加反而减少了。请运用概率统计的相关知识分析分数减少的原因。
解:(1)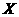 可能取值有
可能取值有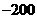 ,10,20,100
,10,20,100
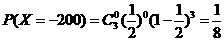 ,
,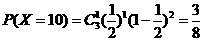 ,
,
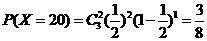 ,
,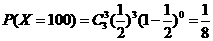
故分布列为
|
| 10 | 20 | 100 |
P |
|
|
|
|
(2)由(1)知:每盘游戏出现音乐的概率是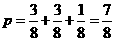
则玩三盘游戏,至少有一盘出现音乐的概率是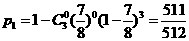
(3)由(1)知,每盘游戏获得的分数为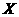 的数学期望是
的数学期望是
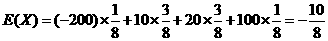 分
分
这说明每盘游戏平均得分是负分,由概率统计的相关知识可知:许多人经过若干盘游戏后,与最初的分数相比,分数没有增加反而会减少。
18.三棱锥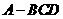 及其侧视图、俯视图如图所示。设
及其侧视图、俯视图如图所示。设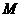 ,
,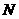 分别为线段
分别为线段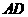 ,
,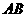 的中点,
的中点,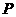 为线段
为线段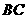 上的点,且
上的点,且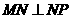 。
。
(1)证明: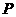 为线段
为线段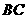 的中点;
的中点;
(2)求二面角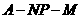 的余弦值。
的余弦值。
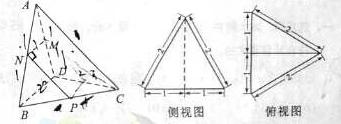
解:(1)由三棱锥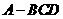 及其侧视图、俯视图可知,在三棱锥
及其侧视图、俯视图可知,在三棱锥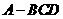 中:
中:
平面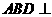 平面
平面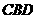 ,
,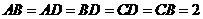
设 为
为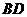 的中点,连接
的中点,连接 ,
,
于是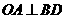 ,
,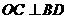 所以
所以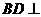 平面
平面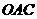
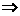
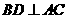
因为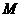 ,
,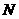 分别为线段
分别为线段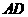 ,
,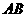 的中点,所以
的中点,所以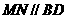 ,又
,又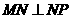 ,故
,故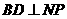
假设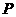 不是线段
不是线段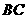 的中点,则直线
的中点,则直线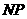 与直线
与直线 是平面
是平面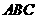 内相交直线
内相交直线
从而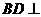 平面
平面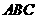 ,这与
,这与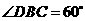 矛盾
矛盾
所以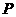 为线段
为线段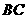 的中点
的中点
(2)以 为坐标原点,
为坐标原点,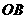 、
、 、
、 分别为
分别为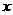 、
、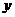 、
、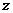 轴建立空间直角坐标系,
轴建立空间直角坐标系,
则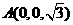 ,
,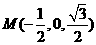 ,
,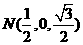 ,
,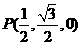
于是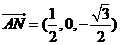 ,
,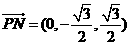 ,
,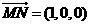
设平面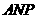 和平面
和平面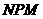 的法向量分别为
的法向量分别为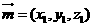 和
和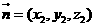
由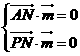
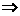
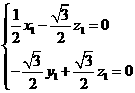 ,设
,设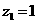 ,则
,则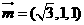
由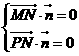
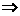
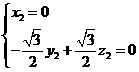 ,设
,设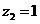 ,则
,则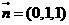
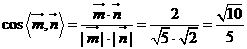
所以二面角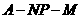 的余弦值
的余弦值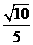
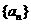 的公差为
的公差为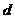 ,点
,点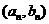 在函数
在函数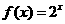 的图象上(
的图象上(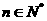 )。
)。(1)若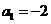 ,点
,点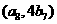 在函数
在函数 的图象上,求数列
的图象上,求数列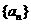 的前
的前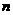 项和
项和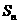 ;
;
(2)若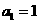 ,函数
,函数 的图象在点
的图象在点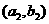 处的切线在
处的切线在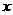 轴上的截距为
轴上的截距为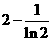 ,求数列
,求数列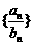 的前
的前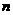 项和
项和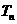 。
。
解:(1)点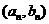 在函数
在函数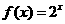 的图象上,所以
的图象上,所以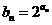 ,又等差数列
,又等差数列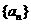 的公差为
的公差为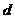
所以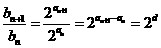
因为点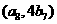 在函数
在函数 的图象上,所以
的图象上,所以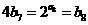 ,所以
,所以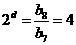
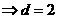
又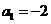 ,所以
,所以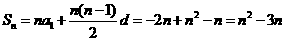
(2)由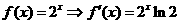
函数 的图象在点
的图象在点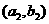 处的切线方程为
处的切线方程为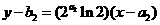
所以切线在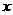 轴上的截距为
轴上的截距为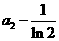 ,从而
,从而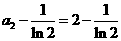 ,故
,故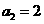
从而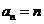 ,
,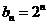 ,
,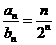
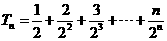
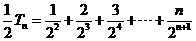
所以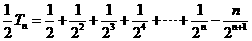
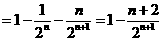
故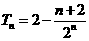
20.已知椭圆C: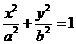 (
(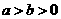 )的焦距为4,其短轴的两个端点与长轴的一个端点构成正三角形。
)的焦距为4,其短轴的两个端点与长轴的一个端点构成正三角形。
(1)求椭圆C的标准方程;
(2)设F为椭圆C的左焦点,T为直线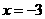 上任意一点,过F作TF的垂线交椭圆C于点P,Q。
上任意一点,过F作TF的垂线交椭圆C于点P,Q。
(i)证明:OT平分线段PQ(其中O为坐标原点);
(ii)当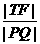 最小时,求点T的坐标。
最小时,求点T的坐标。
解:(1)依条件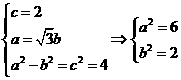
所以椭圆C的标准方程为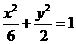
(2)设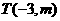 ,
,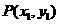 ,
,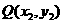 ,又设
,又设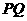 中点为
中点为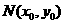
(i)因为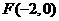 ,所以直线
,所以直线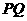 的方程为:
的方程为: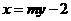
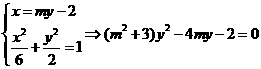
所以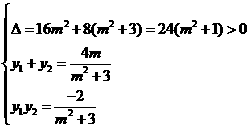
于是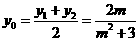 ,
,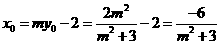
所以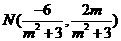 。因为
。因为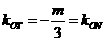
所以 ,
,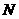 ,
,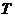 三点共线
三点共线
即OT平分线段PQ(其中O为坐标原点)
(ii)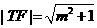 ,
,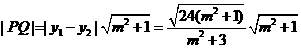
所以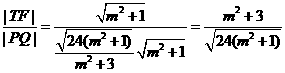 ,令
,令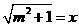 (
(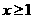 )
)
则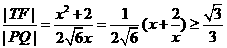 (当且仅当
(当且仅当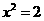 时取“
时取“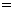 ”)
”)
所以当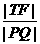 最小时,
最小时,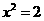 即
即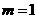 或
或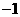 ,此时点T的坐标为
,此时点T的坐标为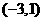 或
或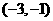
21.已知函数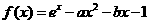 ,其中
,其中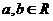 ,
,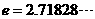 为自然对数的底数。
为自然对数的底数。
(1)设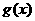 是函数
是函数 的导函数,求函数
的导函数,求函数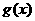 在区间
在区间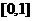 上的最小值;
上的最小值;
(2)若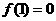 ,函数
,函数 在区间
在区间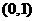 内有零点,求
内有零点,求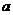 的取值范围
的取值范围
解:(1)因为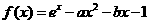 所以
所以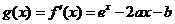 又
又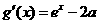
因为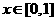 ,
,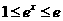 所以:
所以:
①若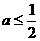 ,则
,则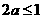 ,
,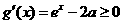 ,
,
所以函数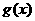 在区间
在区间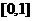 上单增,
上单增,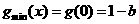
②若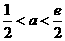 ,则
,则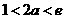 ,
,
于是当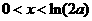 时
时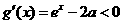 ,当
,当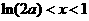 时
时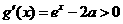 ,
,
所以函数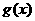 在区间
在区间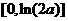 上单减,在区间
上单减,在区间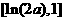 上单增,
上单增,
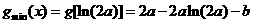
③若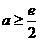 ,则
,则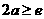 ,
,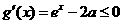
所以函数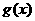 在区间
在区间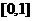 上单减,
上单减,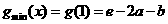
综上: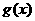 在区间
在区间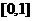 上的最小值为
上的最小值为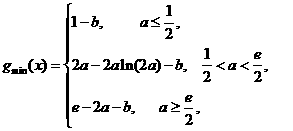
(2)由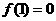
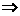
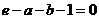
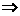
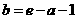 ,又
,又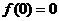
若函数 在区间
在区间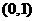 内有零点,则函数
内有零点,则函数 在区间
在区间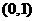 内至少有三个单调区间
内至少有三个单调区间
由(1)知当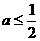 或
或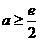 时,函数
时,函数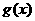 即
即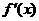 在区间
在区间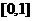 上单调,不可能满足“函数
上单调,不可能满足“函数 在区间
在区间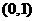 内至少有三个单调区间”这一要求。
内至少有三个单调区间”这一要求。
若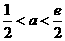 ,则
,则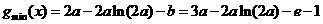
令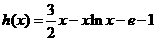 (
(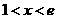 )
)
则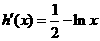 。由
。由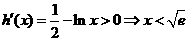
所以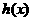 在区间
在区间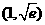 上单增,在区间
上单增,在区间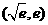 上单减
上单减
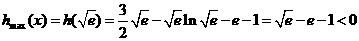 即
即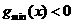 恒成立
恒成立
于是,函数 在区间
在区间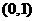 内至少有三个单调区间
内至少有三个单调区间
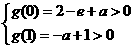
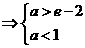
又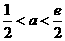 所以
所以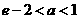
综上,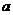 的取值范围为
的取值范围为