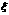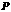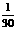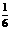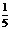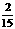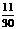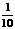一、选择题:本大题共10小题,每小题5分.在每小题给出的四个选项中,只有一项是符合题目要求的.
(1)已知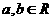 ,
,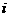 是虚数单位,若
是虚数单位,若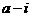 与
与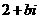 互为共轭复数,则
互为共轭复数,则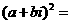
(A)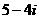 (B)
(B)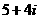 (C)
(C)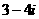 (D)
(D)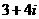
(2)设集合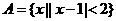 ,
,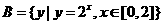 ,则
,则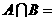
(A)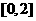 (B)
(B)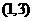 (C)
(C)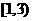 (D)
(D)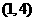
(3)函数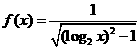 的定义域为
的定义域为
(A)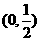 (B)
(B)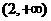 (C)
(C)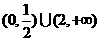 (D)
(D)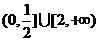
(4)用反证法证明命题:“已知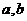 为实数,则方程
为实数,则方程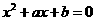 至少有一个实根”时,要做的假设是
至少有一个实根”时,要做的假设是
(A)方程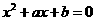 没有实根(B)方程
没有实根(B)方程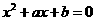 至多有一个实根
至多有一个实根
(C)方程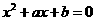 至多有两个实根(D)方程
至多有两个实根(D)方程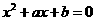 恰好有两个实根
恰好有两个实根
(5)已知实数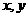 满足
满足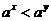 (
(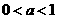 ),则下列关系式恒成立的是
),则下列关系式恒成立的是
(A)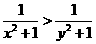 (B)
(B)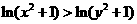
(C)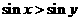 (D)
(D)
(6)直线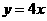 与曲线
与曲线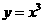 在第一象限内围成的封闭图形的面积为
在第一象限内围成的封闭图形的面积为
(A)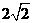 (B)
(B)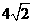 (C)2(D)4
(C)2(D)4
(7)为研究某药品的疗效,选取若干名志愿者进行临床试验,所有志愿者的舒张压数据(单位: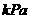 )的分组区间为
)的分组区间为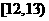 ,
,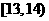 ,
,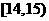 ,
,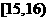 ,
,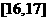 ,将其按从左到右的顺序分别编号为第一组,第二组,......,第五组.右图是根据试验数据制成的频率分布直方图.已知第一组与第二组共有20人,第三组中没有疗效的有6人,则第三组中有疗效的人数为
,将其按从左到右的顺序分别编号为第一组,第二组,......,第五组.右图是根据试验数据制成的频率分布直方图.已知第一组与第二组共有20人,第三组中没有疗效的有6人,则第三组中有疗效的人数为
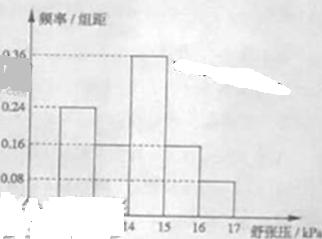
(A)1(B)8(C)12(D)18
(8)已知函数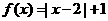 ,
,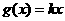 ,若
,若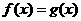 有两个不相等的实根,则实数
有两个不相等的实根,则实数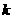 的取值范围是
的取值范围是
(A)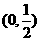 (B)
(B)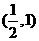 (C)
(C)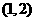 (D)
(D)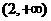
(9)已知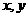 满足约束条件
满足约束条件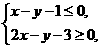 当目标函数
当目标函数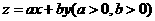 在该约束条件下取到最小值
在该约束条件下取到最小值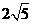 时,
时,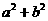 的最小值为
的最小值为
(A)5(B)4(C)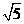 (D)2
(D)2
(10)已知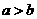 ,椭圆
,椭圆 的方程为
的方程为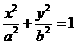 ,双曲线
,双曲线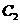 的方程为
的方程为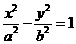 ,
, 与
与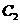 的离心率之积为
的离心率之积为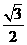 ,则
,则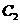 的渐近线方程为
的渐近线方程为
(A)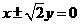 (B)
(B)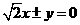 (C)
(C)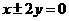 (D)
(D)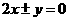
二、填空题:本大题共5小题,每小题5分,共25分
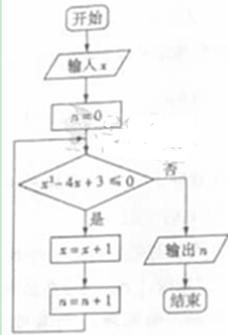
(11)执行右面的程序框图,若输入的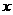 的值为1,则输出的
的值为1,则输出的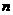 的值为__________ .
的值为__________ .
(12)在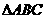 中,已知
中,已知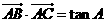 ,当
,当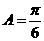 时,
时,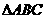 的面积为__________ .
的面积为__________ .
(13)三棱锥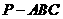 中,
中,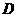 ,
,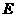 分别为
分别为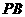 ,
,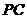 的中点,记三棱锥
的中点,记三棱锥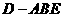 的体积为
的体积为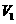 ,
,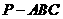 的体积为
的体积为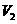 ,则
,则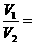 __________ .
__________ .
(14)若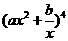 的展开式中
的展开式中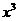 项的系数为20,则
项的系数为20,则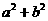 的最小值为 __________ .
的最小值为 __________ .
(15)已知函数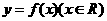 .对函数
.对函数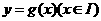 ,定义
,定义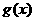 关于
关于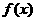 的“对称函数”为
的“对称函数”为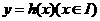 ,
,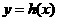 满足:对任意
满足:对任意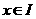 ,两个点
,两个点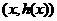 ,
,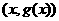 关于点
关于点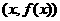 对称.若
对称.若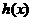 是
是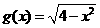 关于
关于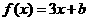 的“对称函数”,且
的“对称函数”,且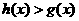 恒成立,则实数
恒成立,则实数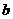 的取值范围是 __________.
的取值范围是 __________.
三、解答题:本大题共6小题,共75分.
(16)(本小题满分12分)
已知向量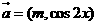 ,
,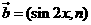 ,设函数
,设函数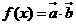 ,且
,且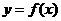 的图象过点
的图象过点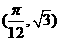 和点
和点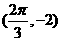 .
.
(Ⅰ)求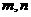 的值;
的值;
(Ⅱ)将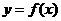 的图象向左平移
的图象向左平移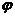 (
(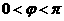 )个单位后得到函数
)个单位后得到函数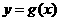 的图象.若
的图象.若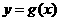 的图象上各最高点到点
的图象上各最高点到点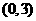 的距离的最小值为1,求
的距离的最小值为1,求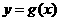 的单调增区间.
的单调增区间.
(17)(本小题满分12分)
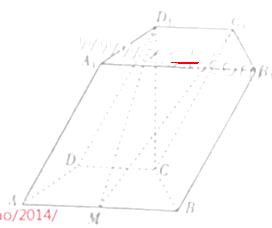
如图,在四棱柱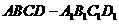 中,底面
中,底面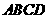 是等腰梯形,
是等腰梯形,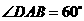 ,
,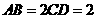 ,
,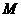 是线段
是线段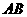 的中点.
的中点.
(Ⅰ)求证: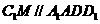 ;
;
(Ⅱ)若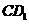 垂直于平面
垂直于平面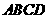 且
且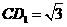 ,求平面
,求平面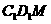 和平面
和平面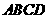 所成的角(锐角)的余弦值.
所成的角(锐角)的余弦值.
(18)(本小题满分12分)
乒乓球台面被网分成甲、乙两部分,如图,
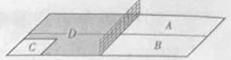
甲上有两个不相交的区域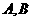 ,乙被划分为两个不相交的区域
,乙被划分为两个不相交的区域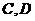 .某次测试要求队员接到落点在甲上的来球后向乙回球.规定:回球一次,落点在
.某次测试要求队员接到落点在甲上的来球后向乙回球.规定:回球一次,落点在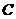 上记3分,在
上记3分,在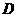 上记1分,其它情况记0分.对落点在
上记1分,其它情况记0分.对落点在 上的来球,小明回球的落点在
上的来球,小明回球的落点在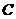 上的概率为
上的概率为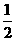 ,在
,在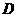 上的概率为
上的概率为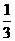 ;对落点在
;对落点在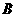 上的来球,小明回球的落点在
上的来球,小明回球的落点在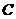 上的概率为
上的概率为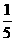 ,在
,在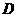 上的概率为
上的概率为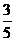 .假设共有两次来球且落在
.假设共有两次来球且落在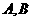 上各一次,小明的两次回球互不影响.求:
上各一次,小明的两次回球互不影响.求:
(Ⅰ)小明的两次回球的落点中恰有一次的落点在乙上的概率;
(Ⅱ)两次回球结束后,小明得分之和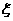 的分布列与数学期望.
的分布列与数学期望.
(19)(本小题满分12分)
已知等差数列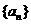 的公差为2,前
的公差为2,前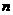 项和为
项和为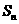 ,且
,且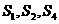 成等比数列.
成等比数列.
(Ⅰ)求数列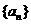 的通项公式;
的通项公式;
(Ⅱ)令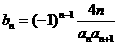 ,求数列
,求数列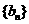 的前
的前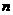 项和
项和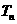 .
.
(20)(本小题满分13分)
设函数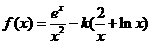 (
(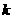 为常数,
为常数,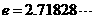 是自然对数的底数).
是自然对数的底数).
(Ⅰ)当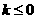 时,求函数
时,求函数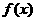 的单调区间;
的单调区间;
(Ⅱ)若函数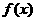 在
在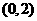 内存在两个极值点,求
内存在两个极值点,求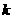 的取值范围.
的取值范围.
(21)(本小题满分14分)
已知抛物线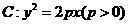 的焦点为
的焦点为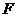 ,
, 为
为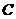 上异于原点的任意一点,过点
上异于原点的任意一点,过点 的直线
的直线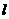 交
交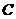 于另一点
于另一点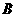 ,交
,交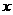 轴的正半轴于点
轴的正半轴于点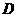 ,且有
,且有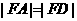 .当点
.当点 的横坐标为3时,
的横坐标为3时, 为正三角形.
为正三角形.
(Ⅰ)求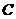 的方程;
的方程;
(Ⅱ)若直线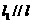 ,且
,且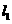 和
和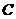 有且只有一个公共点
有且只有一个公共点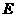 ,
,
(ⅰ)证明直线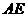 过定点,并求出定点坐标;
过定点,并求出定点坐标;
(ⅱ)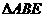 的面积是否存在最小值?若存在,请求出最小值;若不存在,请说明理由.
的面积是否存在最小值?若存在,请求出最小值;若不存在,请说明理由.
2014年山东高考数学(理科)试题解析
第Ⅰ卷(共50分)
一、选择题:本大题共10个小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.【答案】D
【解析】
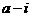 与
与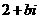 互为共轭复数,
互为共轭复数,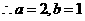
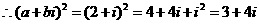
2.【答案】C
【解析】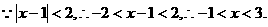
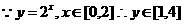
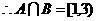
3.【答案】C
【解析】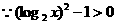
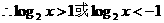
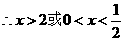
4.【答案】A
【解析】“至少有一个”的对立面应是“没有”,故选A
5.【答案】D
【解析】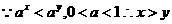 但不能判断
但不能判断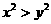 (如
(如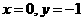 )
) 排除A,B;
排除A,B;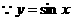 是周期函数,
是周期函数, 排除C;
排除C;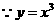 是单调递增函数,
是单调递增函数, D正确.
D正确.
6.【答案】D
【解析】联立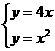 ,且在第一象限,得
,且在第一象限,得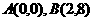
 所求面积
所求面积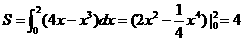
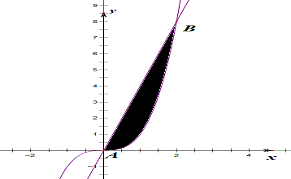
7.【答案】C
【解析】第一组与第二组频率之和为0.24+0.16=0.4,
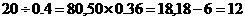
8.【答案】B
【解析】画出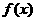 的图像,最低点是
的图像,最低点是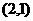 ,
,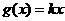 过原点和
过原点和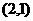 时斜率最小为
时斜率最小为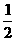 ;斜率最大时
;斜率最大时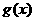 的斜率与
的斜率与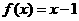 的斜率一致.
的斜率一致.
9.【答案】B
【解析】联立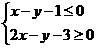 ,得交点坐标
,得交点坐标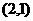 ,则
,则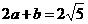 ,即圆心(0,0)到直线
,即圆心(0,0)到直线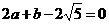 的距离的平方
的距离的平方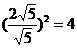 .
.
10.【答案】A
【解析】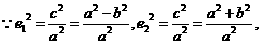
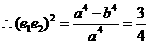
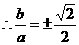
第Ⅱ卷(共100分)
二、填空题(每题5分,满分25分,将答案填在答题纸上)
11.【答案】3
【解析】根据判断条件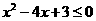 ,得
,得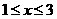
输入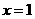
第一次判断后循环,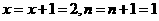
第二次判断后循环,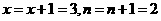
第三次判断后循环,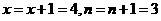
第四次判断不满足条件,结束循环,输出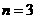
12.【答案】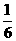
【解析】由条件可知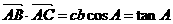 当
当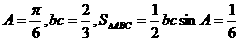
13.【答案】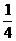
【解析】分别过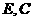 向平面PAB做高
向平面PAB做高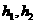 ,由
,由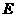 为
为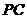 的中点得
的中点得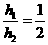 ,
,
由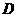 为
为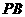 的中点得
的中点得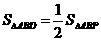 ,所以
,所以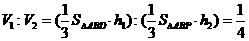
14.【答案】2
【解析】将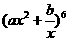 展开,得到
展开,得到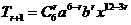 ,令
,令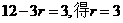 .
.
由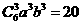 ,得
,得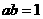 ,所以
,所以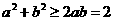 .
.
15.【答案】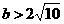
【解析】由题意得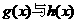 的图像位于直线
的图像位于直线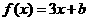 的两侧,要使
的两侧,要使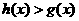 恒成立,则
恒成立,则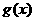 的图像应位于直线
的图像应位于直线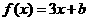 的右下方.根据图像分析得,当
的右下方.根据图像分析得,当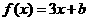 与
与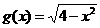 在第二象限相切时,
在第二象限相切时,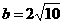 ,由
,由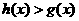 恒成立得
恒成立得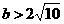 .
.
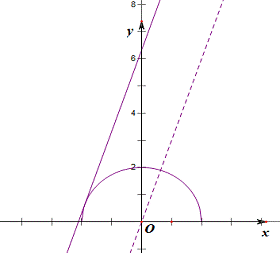
三.解答题:本大题共6小题,共75分,解答应写出文字说明、证明过程或演算步骤。
16.解:(Ⅰ)已知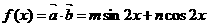 ,
,
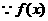 过点
过点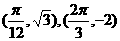

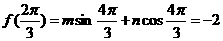
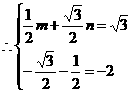 解得
解得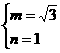
(Ⅱ)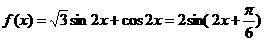
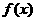 左移
左移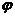 后得到
后得到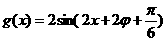
设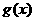 的对称轴为
的对称轴为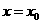 ,
,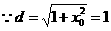 解得
解得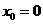
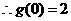 ,解得
,解得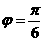
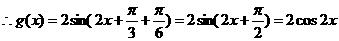
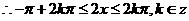
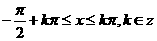
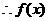 的单调增区间为
的单调增区间为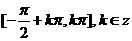
17.解:(Ⅰ)连接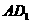
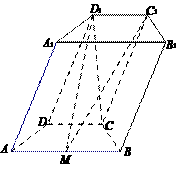
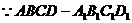 为四棱柱,
为四棱柱,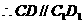
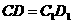
又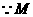 为
为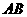 的中点,
的中点,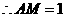
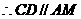 ,
,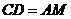
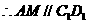 ,
,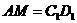
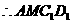 为平行四边形
为平行四边形
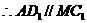
又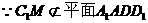
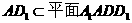
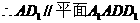
(Ⅱ)方法一: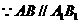
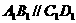
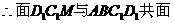
作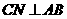 ,连接
,连接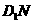
则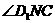 即为所求二面角
即为所求二面角
在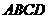 中,
中,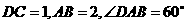
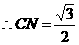
在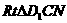 中,
中,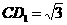 ,
,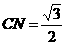
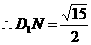
方法二:作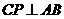 于
于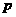 点
点
以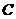 为原点,
为原点,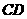 为
为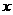 轴,
轴,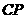 为
为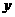 轴,
轴,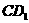 为
为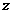 轴建立空间坐标系,
轴建立空间坐标系,
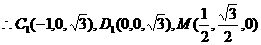
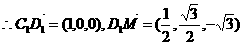
设平面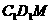 的法向量为
的法向量为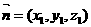
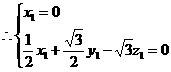
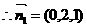
显然平面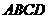 的法向量为
的法向量为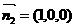
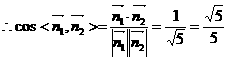 .
.
显然二面角为锐角,
所以平面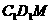 和平面
和平面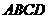 所成角的余弦值为
所成角的余弦值为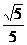
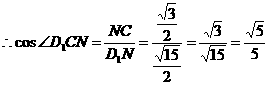
18.解:(I)设恰有一次的落点在乙上这一事件为
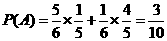
(II)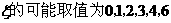
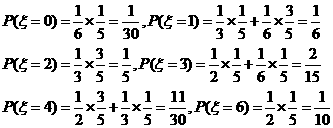
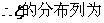
| 0 | 1 | 2 | 3 | 4 | 6 |
|
|
|
|
|
|
|
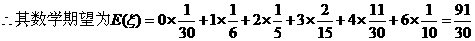 .
.
19.解:(I)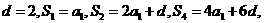

解得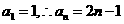
(II)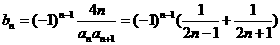
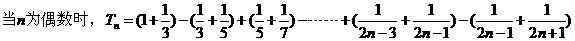
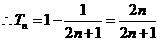
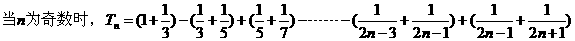
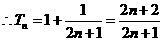
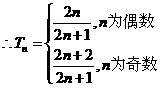
解:(I)函数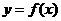 的定义域为
的定义域为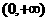
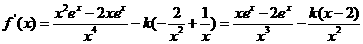
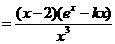
由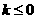 可得
可得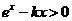 ,
,
所以 当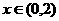 时,
时,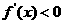 ,函数
,函数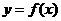 单调递减,
单调递减,
当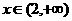 时,
时,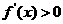 ,函数
,函数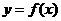 单调递增,
单调递增,
所以,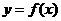 的单调递减区间为
的单调递减区间为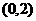 ,单调递增区间为
,单调递增区间为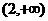 .
.
(II)由(I)知,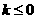 时,函数
时,函数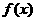 在
在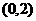 内单调递减,
内单调递减,
所以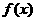 在
在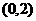 内不存在极值点;
内不存在极值点;
当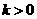 时,设函数
时,设函数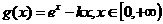 .
.
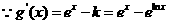 ,
,
当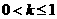 时,当
时,当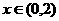 时,
时,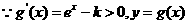 单调递增.
单调递增.
所以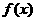 在
在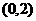 内不存在两个极值点;
内不存在两个极值点;
当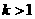 时,得:当
时,得:当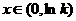 时,
时,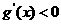 ,函数
,函数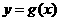 单调递减,
单调递减,
当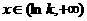 时,
时,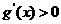 ,函数
,函数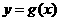 单调递增.
单调递增.
所以函数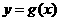 的最小值为
的最小值为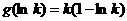 .
.
函数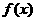 在
在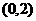 内存在两个极值点,当且仅当
内存在两个极值点,当且仅当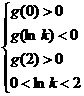
解得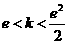
综上所述,函数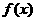 在
在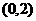 内存在两个极值点时,
内存在两个极值点时,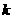 的取值范围为
的取值范围为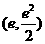 .
.
解:(I)由题意知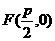 .
.
设,则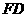 的中点为
的中点为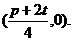
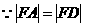 ,由抛物线的定义知
,由抛物线的定义知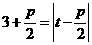 ,
,
解得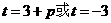 (舍去)
(舍去)
由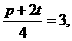 解得
解得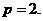
所以抛物线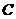 的方程为
的方程为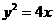 .
.
(II)(i)由(I)知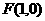
设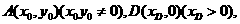
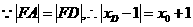 ,
,
由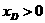 得
得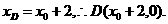
所以直线AB的斜率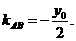
因为直线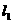 与直线AB平行,
与直线AB平行,
所以设直线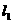 的方程为
的方程为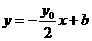 ,
,
代入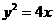 ,得
,得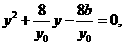
由题意得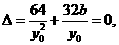 得
得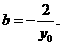
设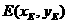 ,则
,则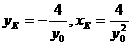 .
.
当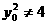 时,
时,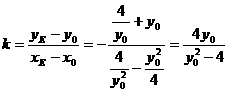 ,
,
由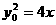 ,整理得
,整理得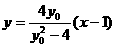 ,
,
直线AE恒过点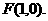
当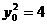 时,直线AE的方程为
时,直线AE的方程为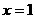 ,过点
,过点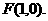
所以 直线AE过定点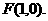
(ii)由(i)得直线AE过焦点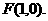
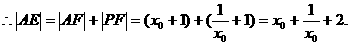
设直线AE的方程为
因为点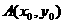 在直线AE上,
在直线AE上,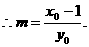
设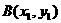 ,直线AB的方程为
,直线AB的方程为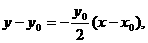
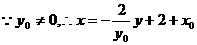 ,
,
代入抛物线方程,得: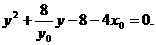
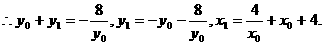
所以点B到直线AE的距离为
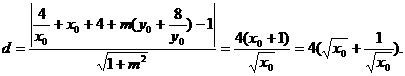
则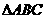 的面积
的面积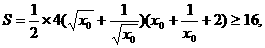
当且仅当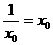 ,即
,即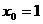 时等号成立.
时等号成立.
所以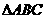 的面积的最小值为16.
的面积的最小值为16.