一、选择题:本大题共12小题,每小题5分,共60分。每小题给出的四个选项中,只有一项是符合题目要求的。
(1)集合A={0,2,a},B={1,a2}.若A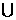 B={0,1,2,4,16},则a的值为
B={0,1,2,4,16},则a的值为
(A)0 (B)1 (C)2 (D)4
(2)复数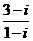 等于
等于
(A)1+2i (B)1-2i (C)2 +i (D)2 – i
(3) 将函数y=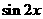 的图像向左平移
的图像向左平移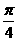 个单位,再向上平移1个单位,所得图像的函数解析式是
个单位,再向上平移1个单位,所得图像的函数解析式是
(A)y=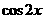 (B)y=
(B)y=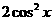
(C)y=1+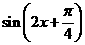 (D)y=
(D)y=
(4)一空间几何体的三视图如图所示,则该几何体的体积为
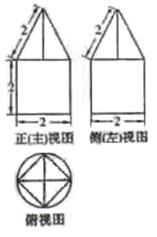
(A)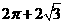 (B)
(B)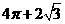
(C)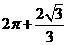 (D)
(D)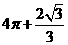
(5)已知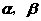 表示两个不同的平面,m为平面
表示两个不同的平面,m为平面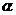 内的一条直线,则“
内的一条直线,则“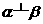 ”是“
”是“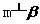 ”的
”的
(A)充分不必要条件 (B)必要不充分条件
(C)充要条件 (D)既不充分也不必要条件
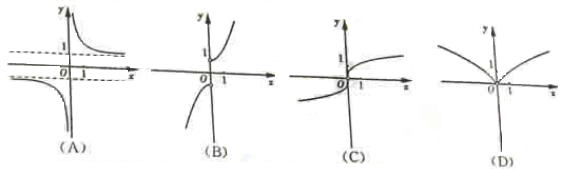
(6)函数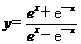 的图象大致为
的图象大致为
(7)设p是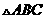 所在平面内的一点,
所在平面内的一点,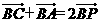 ,则
,则
(A)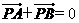
 (B)
(B)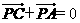
(C)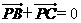 (D)
(D)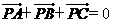
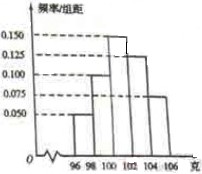
(8)某工厂对一批产品进行了抽样检测。右图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是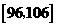 ,样本数据分组为
,样本数据分组为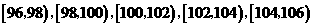
已知样本中产品净重小于100克的个数是36,则样本中净重大于或等于98克并且小于104克的产品的个数是
(A)90 (B)75
(C)60 (D)45
(9)设双曲线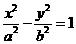 的一条渐近线与抛物线
的一条渐近线与抛物线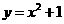 只有一个公共点,则双曲线的离心率为
只有一个公共点,则双曲线的离心率为
(A)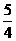 (B)
(B) 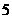 (C)
(C) 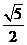 (D)
(D) 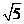
(10) 定义在R上的函数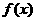 满足
满足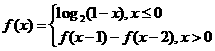 ,则
,则 的值为
的值为
(A)-1 (B) 0 (C) 1 (D) 2
(11)在区间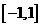 上随机取一个数
上随机取一个数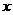 ,
,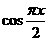 的值介于0到
的值介于0到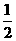 之间的概率为
之间的概率为
(A)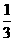 (B)
(B) 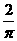 (C)
(C) 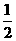 (D)
(D) 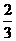
(12)设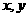 满足约束条件
满足约束条件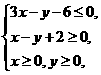 若目标函数
若目标函数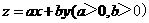 的最大值为12,则
的最大值为12,则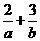 的最小值为
的最小值为
(A)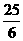 (B)
(B) 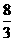 (C)
(C) 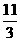 (D) 4
(D) 4
二、填空题:本大题共4小题,每小题4分,共16分. (注意:在试题卷上作答无效)
(13)不等式 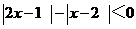 的解集为__________.
的解集为__________.
(14)若函数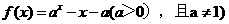 有两个零点,则实数
有两个零点,则实数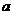 的取值范围是_________.
的取值范围是_________.
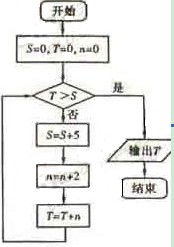
(15)执行右边的程序框图,输出的T=_________.
(16)已知定义在R上的奇函数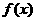 满足
满足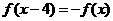 ,且在区间[0,2]上是增函数.若方程
,且在区间[0,2]上是增函数.若方程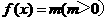 在区间[-8,8]上有四个不同的根
在区间[-8,8]上有四个不同的根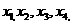 则
则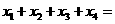 _________.
_________.
三、解答题:本大题共6小题,共74分。
(17)(本小题满分12分)(注意:在试题卷上作答无效)
设函数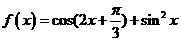 。
。
(Ⅰ)求函数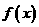 的最大值和最小正周期;
的最大值和最小正周期;
(Ⅱ)设A,B,C为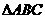 的三个内角,若
的三个内角,若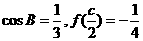 ,且C为锐角,求
,且C为锐角,求
 。
。
(18)(本小题满分12分)(注意:在试题卷上作答无效)
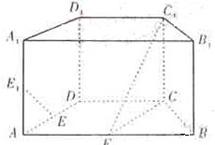
如图,在直四棱柱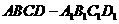 中,底面ABCD为等腰梯形,AB∥CD,AB=4,BC=CD=2,
中,底面ABCD为等腰梯形,AB∥CD,AB=4,BC=CD=2,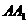 ,AB的中点。
,AB的中点。
(Ⅰ)证明:直线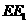 ∥平面
∥平面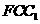 ;
;
(Ⅱ)求二面角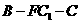 的弦值。
的弦值。
(19)(本小题满分12分) (注意:在试题卷上作答无效)
在某学校组织的一次蓝球定点投蓝训练中,规定每人最多投3次;在A处每投进一球得3分,在B处每投进一球得2分;如果前两次得分之和超过3分即停止投篮,否则投三次。某同学在A处的命中率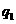 为0.25,在B处的命中率为
为0.25,在B处的命中率为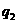 .该同学选择先在A处投一球,以后都在B处投,用
.该同学选择先在A处投一球,以后都在B处投,用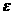 表示该同学投篮训练结束后所得的总分,其分布列为
表示该同学投篮训练结束后所得的总分,其分布列为

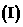 求
求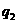 的值;
的值;
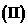 求随机变量
求随机变量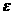 的数学期量
的数学期量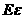 ;
;
 试比较该同学选择都在B处投篮得分超过3分与选择上述方式投篮得分超过3分的概率的大小。
试比较该同学选择都在B处投篮得分超过3分与选择上述方式投篮得分超过3分的概率的大小。
20.(本小题满分12分)(注意:在试题卷上作答无效)
等比数列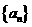 的前n项和为,已知对任意的
的前n项和为,已知对任意的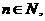 ,点
,点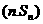 均在函数
均在函数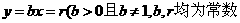 的图象上。
的图象上。
(Ⅰ)求r的值。
(Ⅱ)当b=2时,记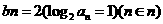 证明:对任意的,不等式成立
证明:对任意的,不等式成立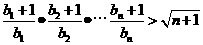
(21)(本小题满分12分)(注意:在试题卷上作答无效)
两县城A和B相距20Km,现计划在两县城外以AB为直径的半圆弧
 上选择一点C建造垃圾理厂,其对城市的影响度与所选地点到城市的距离有关,对城A和城B的总影响度为对城A与对城B的影响度之和。记C点到城A的距离xKm,建在C处的垃圾处理厂对城B的影响度为Y,统计调查表明;垃圾处理厂对城A的影响度与所选地点到城B的平方成反比,比例系数为4;城B的影响度与所选地点到城B的距离的平方成反比,比例系数为K,当垃圾处理厂建在弧
上选择一点C建造垃圾理厂,其对城市的影响度与所选地点到城市的距离有关,对城A和城B的总影响度为对城A与对城B的影响度之和。记C点到城A的距离xKm,建在C处的垃圾处理厂对城B的影响度为Y,统计调查表明;垃圾处理厂对城A的影响度与所选地点到城B的平方成反比,比例系数为4;城B的影响度与所选地点到城B的距离的平方成反比,比例系数为K,当垃圾处理厂建在弧 的中点时,对城A和城B)总影响度为0.065
的中点时,对城A和城B)总影响度为0.065
(Ⅰ)将Y表示成X的函数;
(Ⅱ)讨论(Ⅰ)中函数的单调性,并判断弧 上是否存在一点,使建在此处的垃圾处理厂对城A和城B的总影响度最小?若存在,求出该点城A的距离;若不存在,说明理由。
上是否存在一点,使建在此处的垃圾处理厂对城A和城B的总影响度最小?若存在,求出该点城A的距离;若不存在,说明理由。
(22)(本小题满分14分)(注意:在试题卷上作答无效)
设椭圆E: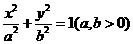
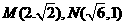 ,O为坐标原点
,O为坐标原点
(Ⅰ)求椭圆E的方程;
(Ⅱ)是否存在圆心在原点的圆,使得该圆的任意一条切线与椭圆E恒在两个交点A,B且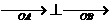 ?若存在,写出该圆的方程,关求
?若存在,写出该圆的方程,关求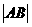 的取值范围;若不存在,说明理由。
的取值范围;若不存在,说明理由。