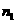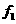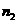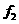一、选择题:本大题共8小题,每小题5分,满分40分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1、已知集合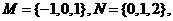 则
则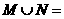
A.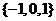 B.
B. 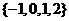
C. 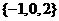 D.
D. 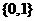
【品题】B.考查集合的并集,目测就可以得出结果.
2、已知复数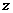 满足
满足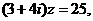 则
则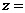
A.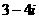 B.
B. 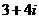 C.
C. 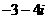 D.
D. 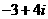
【品题】A.考查复数的运算,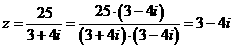
3、若变量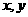 满足约束条件
满足约束条件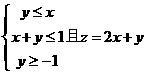 的最大值和最小值分别为
的最大值和最小值分别为 和
和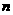 ,则
,则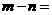
A.8 B.7 C.6 D.5
【品题】C.考查线性规划,求出三条直线的交点为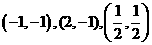 ,故
,故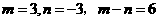
4、若实数k满足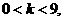 则曲线
则曲线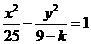 与曲线
与曲线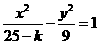 的
的
A.离心率相等 B.虚半轴长相等
C. 实半轴长相等 D.焦距相等
【品题】D.考查双曲线,注意到两条双曲线的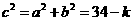 相等,故而选D.
相等,故而选D.
5、已知向量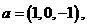 则下列向量中与
则下列向量中与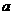 成
成 夹角的是
夹角的是
A.(-1,1,0)B. (1,-1,0)C. (0,-1,1)D. (-1,0,1)
【品题】B.考查向量的夹角与运算,将ABCD四个选项代入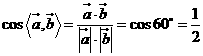 即可选出正确答案
即可选出正确答案
6、已知某地区中小学学生人数和近视情况分别如图1和如图2所示,为了解该地区中下学生的近视形成原因,用分层抽样的方法抽取2%的学生进行调查,则样本容量和抽取的高中生近视人数分别为
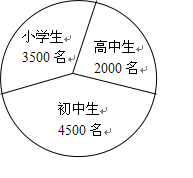
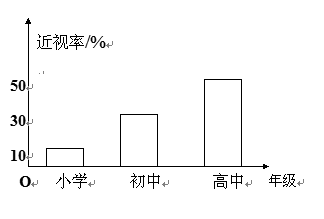
A. 100,10 B. 200,10 C. 100,20 D. 200,20
【品题】D.考查分层抽样.总人数为10000人,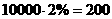 ,其中高中生抽取
,其中高中生抽取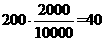 人,故抽取的高中生近视人数为
人,故抽取的高中生近视人数为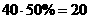 人
人
7、若空间中四条两两不同的直线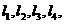 满足
满足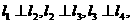 则下面结论一定正确的是
则下面结论一定正确的是
A.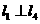 B.
B.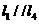 C.
C.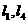 既不垂直也不平行 D.
既不垂直也不平行 D.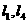 的位置关系不确定
的位置关系不确定
【品题】D.考查空间直线的位置关系.可利用正方体来判断,易得答案.
8、设集合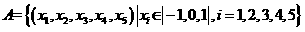 ,那么集合A中满足条件“
,那么集合A中满足条件“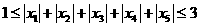 ”的元素个数为
”的元素个数为
A.130 B.120 C.90 D.60
【品题】A.考查分类计数原理、排列组合.先分成3类,4个0、3个0、2个0
(1)4个0
①4个0,1个1: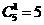
②4个0,1个-1: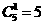
(2)3个0:
①3个0,2个1: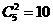
②3个0,1个1,1个-1: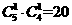
③3个0,2个-1: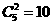
(3)2个0
①2个0,3个1: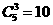
②2个0,2个1,1个-1: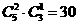
③2个0,1个1,2个-1: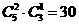
④2个0,3个-1: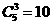
综上所述,所有的可能性有130种
【品味小题】选择很基础了,第8题稍微要一点点细心.答案是BACDBDDA,选项延续了多年答案3221的模式
二、填空题:本大题共7小题.考生作答6小题.每小题5分,满分30分.
(一)必做题(9~13题)
9、不等式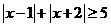 的解集为
的解集为
【品题】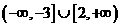 .考查简单的绝对值不等式,用几何意义很快得出答案.
.考查简单的绝对值不等式,用几何意义很快得出答案.
10、曲线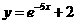 在点
在点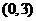 处的切线方程为
处的切线方程为
【品题】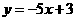 .考查复合函数求导、切线方程.
.考查复合函数求导、切线方程.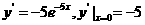 ,故切线方程为
,故切线方程为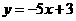 .本题易错点在符合函数求导忘记乘以
.本题易错点在符合函数求导忘记乘以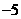 .
.
11、从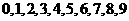 中任取七个不同的数,则这七个数的中位数是6的概率为
中任取七个不同的数,则这七个数的中位数是6的概率为
【品题】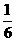 .考查分步技术原理和古典概型.基本事件
.考查分步技术原理和古典概型.基本事件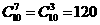 种,包括6且6为中位数的,前3个数从0—5六个数中选3个,后三个数只能是7、8、9,故满足题意的事件有
种,包括6且6为中位数的,前3个数从0—5六个数中选3个,后三个数只能是7、8、9,故满足题意的事件有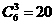 种,从而概率为
种,从而概率为 .本题主要分析准确6为7个数的中位数这个条件就可以很快做出来.
.本题主要分析准确6为7个数的中位数这个条件就可以很快做出来.
12、在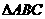 中,角
中,角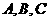 所对应的边分别为
所对应的边分别为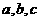 ,已知
,已知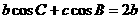 ,
,
则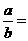
【品题】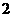 .考查正余弦定理,边角互化.
.考查正余弦定理,边角互化.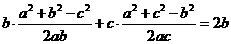 ,化简即可.
,化简即可.
13、若等比数列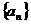 的各项均为正数,且
的各项均为正数,且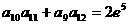 ,
,
则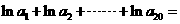
【品题】 .考查等比数列的基础知识.依题意有
.考查等比数列的基础知识.依题意有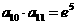 ,所求等式左边
,所求等式左边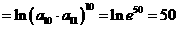
(二)选做题(14、15题,考生只能从中选做一题)
14、(坐标系与参数方程选做题)在极坐标系中,曲线 和
和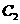 的方程分别为
的方程分别为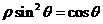 和
和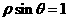 ,以极点为平面直角坐标系的原点,极轴为
,以极点为平面直角坐标系的原点,极轴为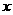 轴正半轴,建立平面直角坐标系,则曲线
轴正半轴,建立平面直角坐标系,则曲线 和
和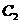 交点的直角坐标为_________
交点的直角坐标为_________

【品题】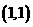 .考查极坐标方程.
.考查极坐标方程.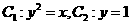 ,联立方程很快得出结果
,联立方程很快得出结果
15、(几何证明选讲选做题)如图3,在平行四边形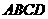 中,
中,
点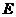 在
在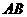 上且
上且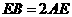 ,
, 与
与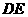 交于点
交于点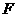 ,
,
则
【品题】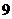 .考查相似三角形面积比等于相似比的平方.
.考查相似三角形面积比等于相似比的平方.
【品填空题】10是易错点、11题有点新意;10、12、13等等是广东07—13年高考考过的.
【品小题】难度适中,出得不错。排列组合除了两题。概率统计考查了很大一个部分,6、11都是概率统计的题目,加大了应用问题的考查,符合新课标的要求,也是2013年高考年报中要求的:加大新课标新双基的力度.没有考查的热点内容包括:算法、三视图、二项式定理、直线与圆的位置关系、回归直线方程等等
三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤.
16、(本小题满分12分)
已知函数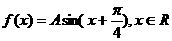 ,且
,且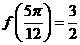 ,
,
(1)求 的值;
的值;
(2)若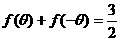 ,
,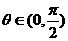 ,求
,求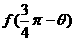 。
。
解:(1)依题意有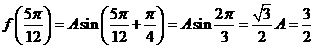 ,所以
,所以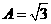
(2)由(1)得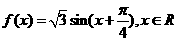 ,
,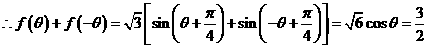
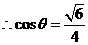 ,
,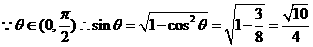
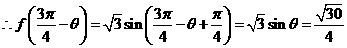
【品题】三角函数延续了08年至今的模式,考查而很基础,有利于稳定考生的得分.
17、(本小题满分13分)
随机观测生产某种零件的某工厂25名工人的日加工零件数(单位:件),获得数据如下:
30,42,41,36,44,40,37,37,25,45,29,43,31,36,49,34,33,43,38,42,32,34,46,39,36
根据上述数据得到样本的频率分布表如下:
分组 | 频数 | 频率 |
[25,30] | 3 | 0.12 |
(30,35] | 5 | 0.20 |
(35,40] | 8 | 0.32 |
(40,45] |
|
|
(45,50] |
|
|
(1)确定样本频率分布表中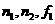 和
和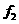 的值;
的值;
(2)根据上述频率分布表,画出样本频率分布直方图;
(3)根据样本频率分布直方图,求在该厂任取4人,至少有1人的日加工零件数落在区间(30,35]的概率.
解:(1)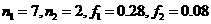
(2)先计算 频率/组距;然后作图即可

(3)由(1)知,任取一人,日加工零件数落在区间(30,35]的概率为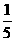
设该厂任取4人,没有人日加工零件数落在区间(30,35]的事件为 ,
,
则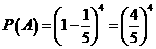 ,所以
,所以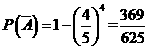
答:在该厂任取4人,至少有1人的日加工零件数落在区间(30,35]的概率为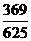
【品题】(1)(2)两问考查了频率分布直方图,包括画图,这个题型主要在于平时练习画图可能不够,以后备考的时候要注意.(3)考查二项分布,不过题意没有明显的标志,相信不少考生感到迷糊,这个考法也是广州一模、二模出过的.
18、(本小题满分13分)
如图4,四边形 为正方形,
为正方形,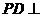 平面
平面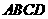 ,
,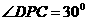 ,
,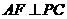 于点
于点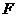 ,
,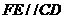 ,交
,交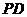 于点
于点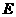 .
.

(1)证明: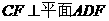
(2)求二面角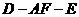 的余弦值
的余弦值