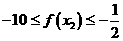一、选择题
(1)设集合A={4,5,7,9},B={3,4,7,8,9},全集U=A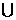 B,则集合
B,则集合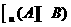 中的元素共有
中的元素共有
(A)3个 (B)4个 (C)5个 (D)6个
(2)已知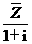 =2+i,则复数z=
=2+i,则复数z=
(A)-1+3i (B)1-3i (C)3+i (D)3-i
(3) 不等式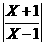 <1的解集为
<1的解集为
(A){x (B)
(B)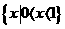
(C)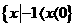 (D)
(D)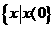
(4)设双曲线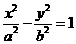 (a>0,b>0)的渐近线与抛物线y=x2 +1相切,则该双曲线的离心率等于
(a>0,b>0)的渐近线与抛物线y=x2 +1相切,则该双曲线的离心率等于
(A)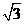 (B)2 (C)
(B)2 (C)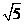 (D)
(D)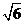
(5) 甲组有5名男同学,3名女同学;乙组有6名男同学、2名女同学。若从甲、乙两组中各选出2名同学,则选出的4人中恰有1名女同学的不同选法共有
(A)150种 (B)180种 (C)300种 (D)345种
(6)设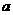 、
、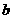 、
、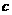 是单位向量,且
是单位向量,且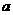 ·
·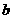 =0,则
=0,则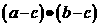 的最小值为
的最小值为
(A)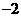 (B)
(B)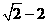 (C)
(C)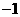 (D)
(D)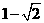
(7)已知三棱柱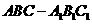 的侧棱与底面边长都相等,
的侧棱与底面边长都相等, 在底面
在底面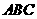 上的射影为
上的射影为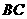 的中点,则异面直线
的中点,则异面直线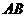 与
与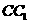 所成的角的余弦值为
所成的角的余弦值为
(A)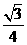 (B)
(B)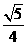 (C)
(C)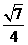 (D)
(D) 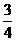
(8)如果函数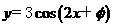 的图像关于点
的图像关于点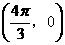 中心对称,那么
中心对称,那么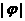 的最小值为
的最小值为
(A)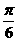 (B)
(B)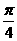 (C)
(C)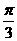 (D)
(D) 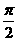
(9) 已知直线y=x+1与曲线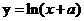 相切,则α的值为
相切,则α的值为
(A)1 (B)2 (C) -1 (D)-2
(10)已知二面角α-l-β为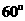 ,动点P、Q分别在面α、β内,P到β的距离为
,动点P、Q分别在面α、β内,P到β的距离为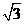 ,Q到α的距离为
,Q到α的距离为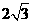 ,则P、Q两点之间距离的最小值为
,则P、Q两点之间距离的最小值为
(A)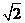 (B)2 (C)
(B)2 (C) 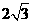 (D)4
(D)4
(11)函数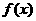 的定义域为R,若
的定义域为R,若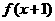 与
与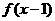 都是奇函数,则
都是奇函数,则
(A) 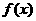 是偶函数 (B)
是偶函数 (B) 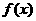 是奇函数
是奇函数
(C) 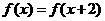 (D)
(D) 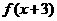 是奇函数
是奇函数
12.已知椭圆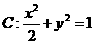 的右焦点为
的右焦点为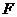 ,右准线为
,右准线为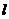 ,点
,点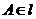 ,线段
,线段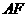 交
交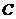 于点
于点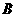 ,若
,若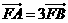 ,则
,则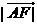 =
=
a. 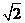 b. 2 C.
b. 2 C.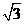 D. 3
D. 3
二、填空题:本大题共4小题,每小题5分,共20分,把答案填在题中横线上。
(注意:在试题卷上作答无效)
13. 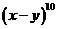 的展开式中,
的展开式中,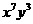 的系数与
的系数与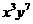 的系数之和等于__________。
的系数之和等于__________。
14. 设等差数列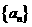 的前
的前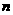 项和为
项和为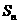 ,若
,若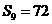 ,则
,则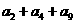 = ________。
= ________。
15. 直三棱柱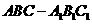 的各顶点都在同一球面上,若
的各顶点都在同一球面上,若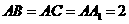 ,
,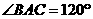 ,则此球的表面积等于________。
,则此球的表面积等于________。
16. 若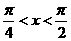 ,则函数
,则函数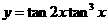 的最大值为 ________。
的最大值为 ________。
三、解答题:本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤。
17(本小题满分10分)(注意:在试题卷上作答无效)
在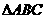 中,内角A、B、C的对边长分别为
中,内角A、B、C的对边长分别为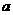 、
、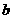 、
、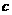 ,已知
,已知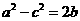 ,且
,且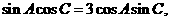 求b
求b
18(本小题满分12分)(注意:在试题卷上作答无效)
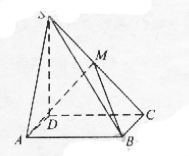
如图,四棱锥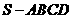 中,底面
中,底面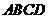 为矩形,
为矩形,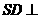 底面
底面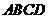 ,
,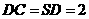 ,点M在侧棱
,点M在侧棱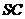 上,
上,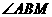 =60°
=60°
(I)证明:M在侧棱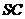 的中点
的中点
(II)求二面角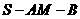 的大小。
的大小。
19(本小题满分12分)(注意:在试题卷上作答无效)
甲、乙二人进行一次围棋比赛,约定先胜3局者获得这次比赛的胜利,比赛结束,假设在一局中,甲获胜的概率为0.6,乙获胜的概率为0.4,各局比赛结果相互独立,已知前2局中,甲、乙各胜1局。
(I)求甲获得这次比赛胜利的概率;
(II)设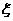 表示从第3局开始到比赛结束所进行的局数,求
表示从第3局开始到比赛结束所进行的局数,求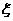 得分布列及数学期望。
得分布列及数学期望。
20(本小题满分12分)(注意:在试题卷上作答无效)
在数列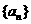 中,
中,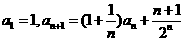
(I)设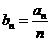 ,求数列
,求数列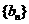 的通项公式
的通项公式
(II)求数列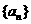 的前
的前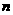 项和
项和
21(本小题满分12分)(注意:在试题卷上作答无效)
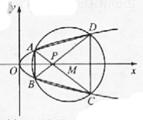
如图,已知抛物线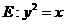 与圆
与圆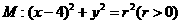 相交于
相交于 、
、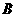 、
、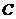 、
、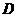 四个点。
四个点。
(I)求 得取值范围;
得取值范围;
(II)当四边形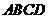 的面积最大时,求对角线
的面积最大时,求对角线 、
、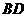 的交点
的交点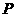 坐标
坐标
22. 本小题满分12分。(注意:在试题卷上作答无效)
设函数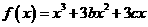 在两个极值点
在两个极值点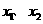 ,且
,且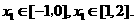
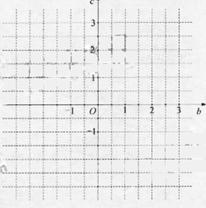
(I)求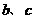 满足的约束条件,并在下面的坐标平面内,画出满足这些条件的点
满足的约束条件,并在下面的坐标平面内,画出满足这些条件的点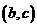 的区域;
的区域;
(II)证明: