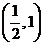非选择题部分(共100分)
二、填空题:本大题共7小题,每小题4分,共28分。
11.设等比数列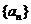 的公比
的公比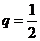 ,前
,前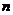 项和为
项和为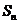 ,则
,则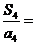 __________.
__________.
答案:15
【解析】对于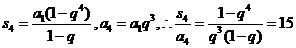
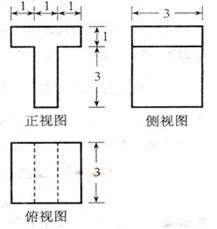
12.若某几何体的三视图(单位: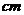 )如图所示,则此几何体的体积是________
)如图所示,则此几何体的体积是________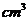 .
.
答案:18
【解析】该几何体是由二个长方体组成,下面体积为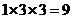 ,上面的长方体体积为
,上面的长方体体积为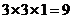 ,因此其几何体的体积为18
,因此其几何体的体积为18
13.若实数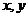 满足不等式组
满足不等式组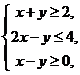 则
则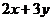 的最小值是_________.
的最小值是_________.

答案:4
【解析】通过画出其线性规划,可知直线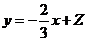 过点
过点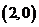 时,
时,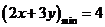
14.某地区居民生活用电分为高峰和低谷两个时间段进行分时计价.该地区的电网销售电价表如
下:
高峰时间段用电价格表 | 低谷时间段用电价格表 | ||
高峰月用电量 (单位:千瓦时) | 高峰电价 (单位:元/千瓦时) | 低谷月用电量 (单位:千瓦时) | 低谷电价 (单位:元/千瓦时) |
50及以下的部分 | 0.568 | 50及以下的部分 | 0.288 |
超过50至200的部分 | 0.598 | 超过50至200的部分 | 0.318 |
超过200的部分 | 0.668 | 超过200的部分 | 0.388 |
若某家庭5月份的高峰时间段用电量为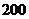 千瓦时,低谷时间段用电量为
千瓦时,低谷时间段用电量为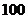 千瓦时,则按这种计费方式该家庭本月应付的电费为 ___________元(用数字作答).
千瓦时,则按这种计费方式该家庭本月应付的电费为 ___________元(用数字作答).

答案: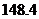
【解析】对于应付的电费应分二部分构成,高峰部分为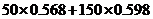 ;对于低峰部分为
;对于低峰部分为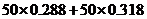 ,二部分之和为
,二部分之和为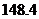
15.观察下列等式:
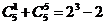 ,
,
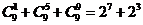 ,
,
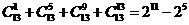 ,
,
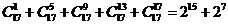 ,
,
………
由以上等式推测到一个一般的结论:
对于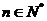 ,
,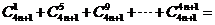 ___________.
___________.

答案: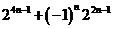
【解析】这是一种需类比推理方法破解的问题,结论由二项构成,第二项前有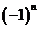 ,二项指数分别为
,二项指数分别为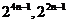 ,因此对于
,因此对于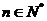 ,
,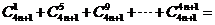
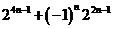
16.甲、乙、丙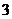 人站到共有
人站到共有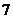 级的台阶上,若每级台阶最多站
级的台阶上,若每级台阶最多站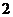 人,同一级台阶上的人不区分站的位置,则不同的站法种数是_____________(用数字作答).
人,同一级台阶上的人不区分站的位置,则不同的站法种数是_____________(用数字作答).
答案:336
【解析】对于7个台阶上每一个只站一人,则有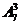 种;若有一个台阶有2人,另一个是1人,则共有
种;若有一个台阶有2人,另一个是1人,则共有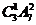 种,因此共有不同的站法种数是336种.
种,因此共有不同的站法种数是336种.

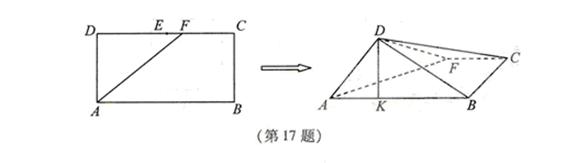
17.如图,在长方形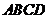 中,
中,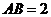 ,
,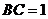 ,
,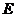 为
为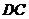 的中点,
的中点,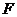 为线段
为线段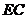 (端点除外)上一动点.现将
(端点除外)上一动点.现将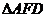 沿
沿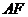 折起,使平面
折起,使平面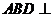 平面
平面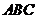 .在平面
.在平面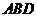 内过点
内过点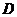
作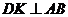 ,
,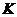 为垂足.设
为垂足.设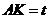 ,则
,则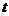 的取值范围是___________.
的取值范围是___________.
答案: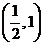
【解析】此题的破解可采用二个极端位置法,即对于F位于DC的中点时,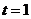 ,随着F点到C点时,因
,随着F点到C点时,因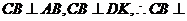 平面
平面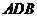 ,即有
,即有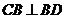 ,对于
,对于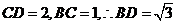 ,又
,又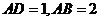 ,因此有
,因此有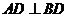 ,则有
,则有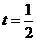 ,因此
,因此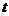 的取值范围是
的取值范围是