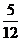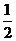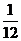三、解答题:本大题共5小题,共72分。解答应写出文字说明、证明过程或演算步骤。
18.(本题满分14分)在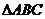 中,角
中,角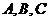 所对的边分别为
所对的边分别为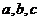 ,且满足
,且满足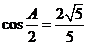 ,
,
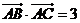 . (I)求
. (I)求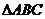 的面积; (II)若
的面积; (II)若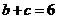 ,求
,求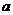 的值.
的值.
解析:(I)因为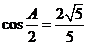 ,
,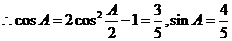 ,又由
,又由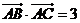 ,得
,得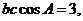
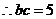 ,
,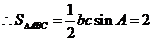


(II)对于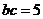 ,又
,又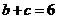 ,
,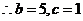 或
或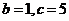 ,由余弦定理得
,由余弦定理得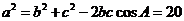 ,
,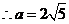


19.(本题满分14分)在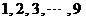 这
这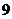 个自然数中,任取
个自然数中,任取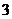 个数.
个数.
(I)求这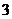 个数中恰有
个数中恰有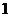 个是偶数的概率;
个是偶数的概率;
(II)设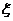 为这
为这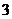 个数中两数相邻的组数(例如:若取出的数为
个数中两数相邻的组数(例如:若取出的数为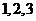 ,则有两组相邻的数
,则有两组相邻的数
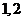 和
和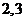 ,此时
,此时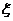 的值是
的值是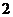 ).求随机变量
).求随机变量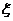 的分布列及其数学期望
的分布列及其数学期望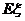 .
.
解析:
(I)记“这3个数恰有一个是偶数”为事件A,则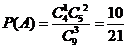 ;
;

(II)随机变量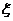 的取值为
的取值为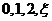 的分布列为
的分布列为
| 0 | 1 | 2 |
P |
|
|
|
所以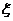 的数学期望为
的数学期望为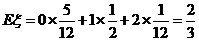


20.(本题满分15分)如图,平面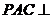 平面
平面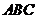 ,
,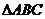 是以
是以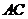 为斜边的等腰直角三角形,
为斜边的等腰直角三角形,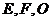 分别为
分别为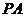 ,
,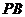 ,
,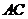 的中点,
的中点,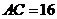 ,
,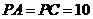 .
.
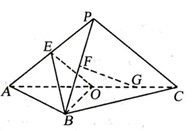
(I)设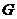 是
是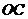 的中点,证明:
的中点,证明: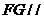 平面
平面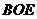 ;
;
(II)证明:在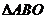 内存在一点
内存在一点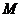 ,使
,使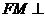 平面
平面 ,并求点
,并求点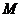 到
到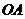 ,
,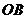 的距离.
的距离.
证明:(I)如图,连结OP,以O为坐标原点,分别以OB、OC、OP所在直线为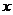 轴,
轴,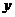 轴,
轴,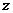 轴,建立空间直角坐标系O
轴,建立空间直角坐标系O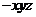 ,
,

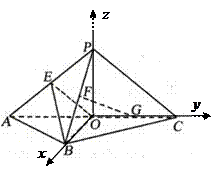
则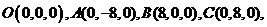
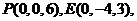
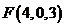 ,由题意得,
,由题意得,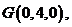 因
因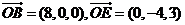 ,因此平面BOE的法向量为
,因此平面BOE的法向量为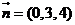 ,
,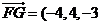 得
得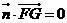 ,又直线
,又直线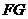 不在平面
不在平面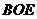 内,因此有
内,因此有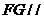 平面
平面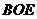
(II)设点M的坐标为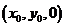 ,则
,则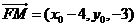 ,因为
,因为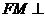 平面BOE,所以有
平面BOE,所以有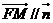 ,因此有
,因此有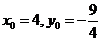 ,即点M的坐标为
,即点M的坐标为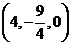 ,在平面直角坐标系
,在平面直角坐标系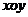 中,
中, 的内部区域满足不等式组
的内部区域满足不等式组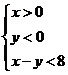 ,经检验,点M的坐标满足上述不等式组,所以在
,经检验,点M的坐标满足上述不等式组,所以在 内存在一点
内存在一点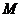 ,使
,使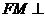 平面
平面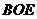 ,由点M的坐标得点
,由点M的坐标得点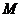 到
到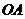 ,
, 的距离为
的距离为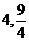 .
.

21.(本题满分15分)已知椭圆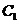 :
: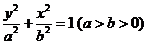 的右顶点为
的右顶点为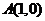 ,过
,过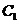 的焦点且垂直长轴的弦长为
的焦点且垂直长轴的弦长为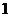 .
.
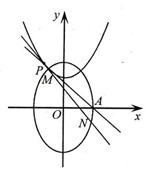
(I)求椭圆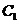 的方程;
的方程;
(II)设点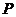 在抛物线
在抛物线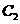 :
: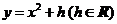 上,
上,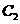 在点
在点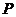 处的切线与
处的切线与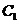 交于点
交于点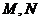 .当线段
.当线段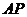 的中点与
的中点与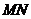 的中点的横坐标相等时,求
的中点的横坐标相等时,求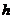 的最小值.
的最小值.
解析:
(I)由题意得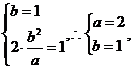 所求的椭圆方程为
所求的椭圆方程为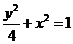 ,
,

(II)不妨设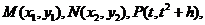 则抛物线
则抛物线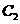 在点P处的切线斜率为
在点P处的切线斜率为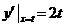 ,直线MN的方程为
,直线MN的方程为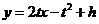 ,将上式代入椭圆
,将上式代入椭圆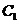 的方程中,得
的方程中,得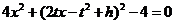 ,即
,即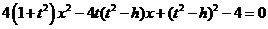 ,因为直线MN与椭圆
,因为直线MN与椭圆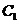 有两个不同的交点,所以有
有两个不同的交点,所以有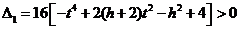 ,
,
设线段MN的中点的横坐标是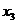 ,则
,则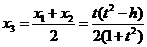 ,
,

设线段PA的中点的横坐标是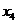 ,则
,则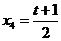 ,由题意得
,由题意得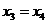 ,即有
,即有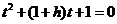 ,其中的
,其中的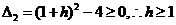 或
或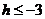 ;
;
当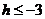 时有
时有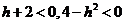 ,因此不等式
,因此不等式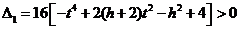 不成立;因此
不成立;因此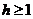 ,当
,当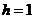 时代入方程
时代入方程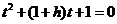 得
得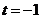 ,将
,将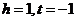 代入不等式
代入不等式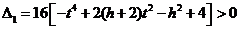 成立,因此
成立,因此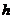 的最小值为1.
的最小值为1.
22.(本题满分14分)已知函数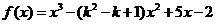 ,
,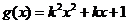 ,
,
其中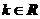 .
.

(I)设函数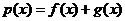 .若
.若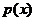 在区间
在区间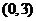 上不单调,求
上不单调,求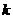 的取值范围;
的取值范围;
(II)设函数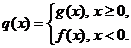 是否存在
是否存在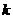 ,对任意给定的非零实数
,对任意给定的非零实数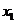 ,存在惟一的非零实数
,存在惟一的非零实数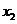 (
(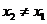 ),使得
),使得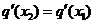 成立?若存在,求
成立?若存在,求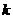 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
解析:(I)因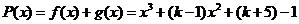 ,
,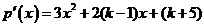 ,因
,因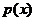 在区间
在区间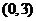 上不单调,所以
上不单调,所以 在
在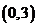 上有实数解,且无重根,由
上有实数解,且无重根,由 得
得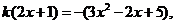


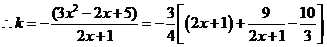 ,令
,令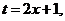 有
有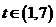 ,记
,记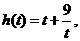 则
则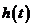 在
在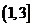 上单调递减,在
上单调递减,在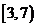 上单调递增,所以有
上单调递增,所以有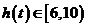 ,于是
,于是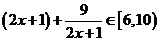 ,得
,得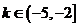 ,而当
,而当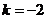 时有
时有 在
在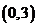 上有两个相等的实根
上有两个相等的实根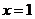 ,故舍去,所以
,故舍去,所以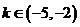 ;
;

(II)当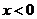 时有
时有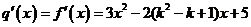 ;
;
当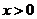 时有
时有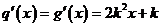 ,因为当
,因为当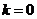 时不合题意,因此
时不合题意,因此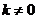 ,
,
下面讨论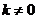 的情形,记A
的情形,记A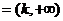 ,B=
,B=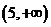 (ⅰ)当
(ⅰ)当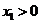 时,
时,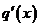 在
在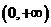 上单调递增,所以要使
上单调递增,所以要使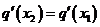 成立,只能
成立,只能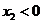 且
且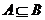 ,因此有
,因此有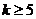 ,(ⅱ)当
,(ⅱ)当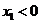 时,
时,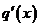 在
在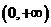 上单调递减,所以要使
上单调递减,所以要使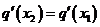 成立,只能
成立,只能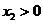 且
且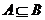 ,因此
,因此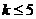 ,综合(ⅰ)(ⅱ)
,综合(ⅰ)(ⅱ)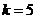 ;
;
当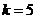 时A=B,则
时A=B,则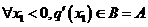 ,即
,即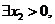 使得
使得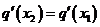 成立,因为
成立,因为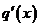 在
在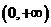 上单调递增,所以
上单调递增,所以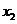 的值是唯一的;
的值是唯一的;
同理,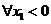 ,即存在唯一的非零实数
,即存在唯一的非零实数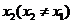 ,要使
,要使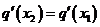 成立,所以
成立,所以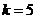 满足题意.
满足题意.