三.解答题:本大题共6小题,共75分,解答应写出文字说明、证明过程或演算步骤.解答写在答题卡的制定区域内.
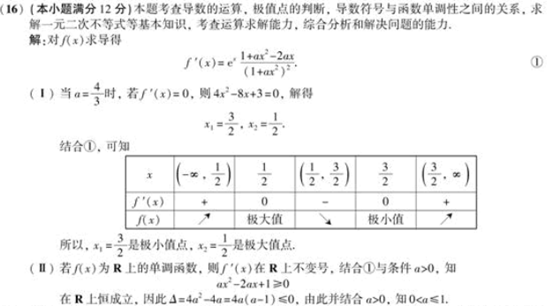
(16)(本小题满分12分)
设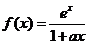
 ,其中
,其中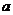 为正实数
为正实数
(Ⅰ)当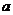
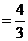 时,求
时,求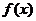 的极值点;
的极值点;
(Ⅱ)若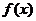 为
为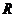 上的单调函数,求
上的单调函数,求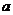 的取值范围。
的取值范围。
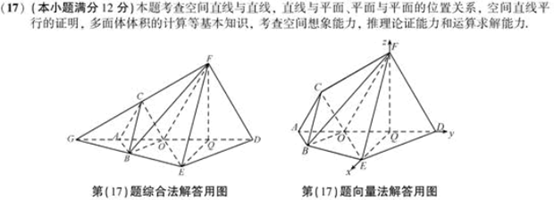
(17)(本小题满分12分)
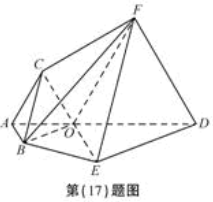
如图,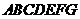 为多面体,平面
为多面体,平面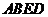 与平面
与平面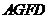 垂直,点
垂直,点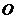 在线段
在线段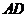 上,
上,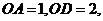
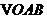 ,△
,△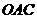 ,△
,△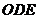 ,△
,△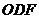 都是正三角形。
都是正三角形。
(Ⅰ)证明直线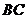 ∥
∥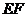 ;
;
(2)求棱锥F—OBED的体积.

(18)(本小题满分13分)
在数1和100之间插入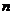 个实数,使得这
个实数,使得这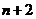 个数构成递增的等比数列,将这
个数构成递增的等比数列,将这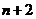 个数的乘积记作
个数的乘积记作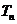 ,再令
,再令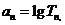
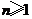 .
.
(Ⅰ)求数列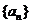 的通项公式;
的通项公式;
(Ⅱ)设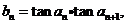 求数列
求数列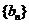 的前
的前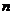 项和
项和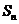 .
.

(19)(本小题满分12分)
(Ⅰ)设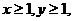 证明
证明
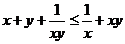 ,
,
(Ⅱ)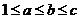 ,证明
,证明
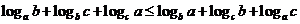 .
.


(20)(本小题满分13分)
工作人员需进入核电站完成某项具有高辐射危险的任务,每次只派一个人进去,且每个人只派一次,工作时间不超过10分钟,如果有一个人10分钟内不能完成任务则撤出,再派下一个人。现在一共只有甲、乙、丙三个人可派,他们各自能完成任务的概率分别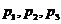
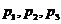 ,假设
,假设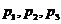 互不相等,且假定各人能否完成任务的事件相互独立.
互不相等,且假定各人能否完成任务的事件相互独立.
(Ⅰ)如果按甲在先,乙次之,丙最后的顺序派人,求任务能被完成的概率。若改变三个人被派出的先后顺序,任务能被完成的概率是否发生变化?
(Ⅱ)若按某指定顺序派人,这三个人各自能完成任务的概率依次为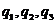 ,其中
,其中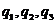 是
是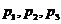 的一个排列,求所需派出人员数目
的一个排列,求所需派出人员数目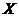 的分布列和均值(数字期望)
的分布列和均值(数字期望)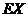 ;
;
(Ⅲ)假定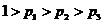 ,试分析以怎样的先后顺序派出人员,可使所需派出的人员数目的均值(数字期望)达到最小。
,试分析以怎样的先后顺序派出人员,可使所需派出的人员数目的均值(数字期望)达到最小。

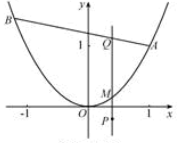
(21)(本小题满分13分)
设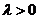 ,点
,点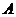 的坐标为(1,1),点
的坐标为(1,1),点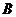 在抛物线
在抛物线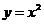 上运动,点
上运动,点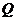 满足
满足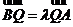 ,经过
,经过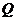 点与
点与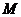
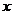 轴垂直的直线交抛物线于点
轴垂直的直线交抛物线于点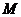 ,点
,点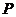 满足
满足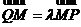 ,求点
,求点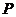 的轨迹方程。
的轨迹方程。