三.解答题:本大题共6小题,共75分。解答应写出文字说明、证明过程或演算步骤。解答写在答题卡上的指定区域内。
(16)(本小题满分12分)
已知函数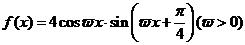 的最小正周期为
的最小正周期为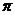 。
。
(Ⅰ)求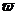 的值;
的值;
(Ⅱ)讨论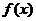 在区间
在区间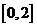 上的单调性。
上的单调性。
【答案】 (Ⅰ) 1
(Ⅱ) 
【解析】 (Ⅰ)
 .所以
.所以
(Ⅱ) 

所以
(17)(本小题满分12分)
设函数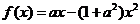 ,其中
,其中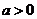 ,区间
,区间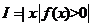
(Ⅰ)求的长度(注:区间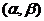 的长度定义为
的长度定义为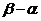 );
);
(Ⅱ)给定常数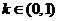 ,当时,求
,当时,求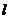 长度的最小值。
长度的最小值。
【答案】 (Ⅰ) 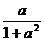 .
.
(Ⅱ) 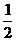
【解析】 (Ⅰ) .所以区间长度为
.所以区间长度为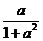 .
.
(Ⅱ) 若
 .
. .
.
(18)(本小题满分12分)
设椭圆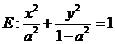 的焦点在
的焦点在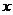 轴上
轴上
(Ⅰ)若椭圆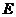 的焦距为1,求椭圆
的焦距为1,求椭圆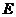 的方程;
的方程;
(Ⅱ)设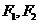 分别是椭圆的左、右焦点,
分别是椭圆的左、右焦点,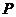 为椭圆
为椭圆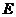 上的第一象限内的点,直线
上的第一象限内的点,直线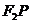 交
交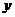 轴与点
轴与点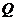 ,并且
,并且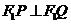 ,证明:当
,证明:当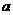 变化时,点
变化时,点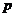 在某定直线上。
在某定直线上。
【答案】 (Ⅰ)  .
.
(Ⅱ) 
【解析】 (Ⅰ)
 .
.
(Ⅱ)  .
.
由 .
.
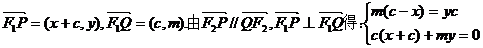
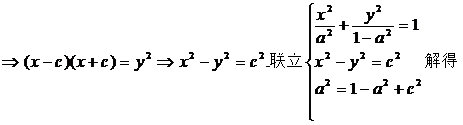
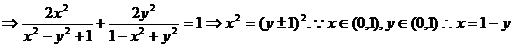
所以动点P过定直线 .
.
(19)(本小题满分13分)
如图,圆锥顶点为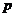 。底面圆心为
。底面圆心为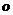 ,其母线与底面所成的角为22.5°。
,其母线与底面所成的角为22.5°。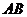 和
和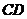 是底面圆
是底面圆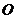 上的两条平行的弦,轴
上的两条平行的弦,轴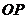 与平面
与平面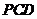 所成的角为60°,
所成的角为60°,
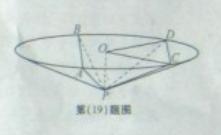
(Ⅰ)证明:平面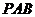 与平面
与平面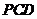 的交线平行于底面;
的交线平行于底面;
(Ⅱ)求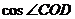 。
。
【答案】 (Ⅰ) 见下.
(Ⅱ) 
【解析】 (Ⅰ) 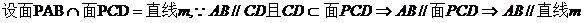
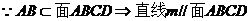 .
.
所以, .(证毕)
.(证毕)
(Ⅱ) 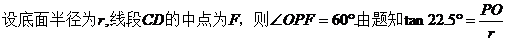 .
.
 .
.

 .(完)
.(完)
(20)(本小题满分13分)
设函数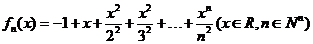 ,证明:
,证明:
(Ⅰ)对每个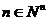 ,存在唯一的
,存在唯一的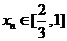 ,满足
,满足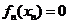 ;
;
(Ⅱ)对任意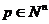 ,由(Ⅰ)中
,由(Ⅰ)中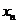 构成的数列
构成的数列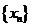 满足
满足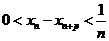 。
。
【答案】 (Ⅰ) 见下. (Ⅱ)见下.
【解析】 (Ⅰ) 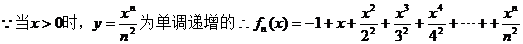 是x的单调递增函数,也是n的单调递增函数.
是x的单调递增函数,也是n的单调递增函数.  .
.

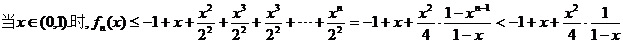

综上,对每个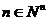 ,存在唯一的
,存在唯一的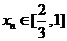 ,满足
,满足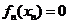 ;(证毕)
;(证毕)
(Ⅱ) 由题知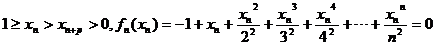
 上式相减:
上式相减:

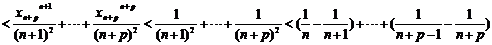

(21)(本小题满分13分)
某高校数学系计划在周六和周日各举行一次主题不同的心理测试活动,分别由李老师和张老师负责,已知该系共有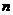 位学生,每次活动均需该系
位学生,每次活动均需该系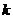 位学生参加(
位学生参加(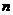 和
和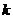 都是固定的正整数)。假设李老师和张老师分别将各自活动通知的信息独立、随机地发给该系
都是固定的正整数)。假设李老师和张老师分别将各自活动通知的信息独立、随机地发给该系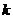 位学生,且所发信息都能收到。记该系收到李老师或张老师所发活动通知信息的学生人数为
位学生,且所发信息都能收到。记该系收到李老师或张老师所发活动通知信息的学生人数为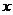
(Ⅰ)求该系学生甲收到李老师或张老师所发活动通知信息的概率;
(Ⅱ)求使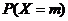 取得最大值的整数
取得最大值的整数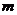 。
。
【答案】 (Ⅰ) 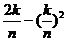 .
.
(Ⅱ) 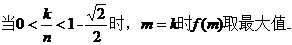

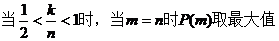
【解析】 (Ⅰ)  .
.
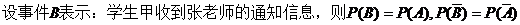 .
.
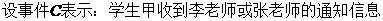 .
.
则 .
.
所以, .
.
(Ⅱ)  ,
,

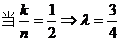 .
.
 ;
;
讨论如下:
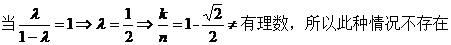 .
.
 .
.
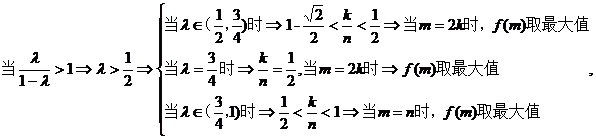 .
.