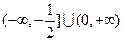19.(本小题满分14分)
设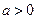 ,讨论函数
,讨论函数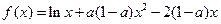 的单调性.
的单调性.
19.解:函数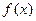 的定义域为
的定义域为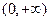
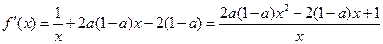
令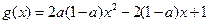
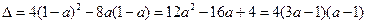
① 当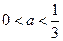 时,
时,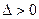 ,令
,令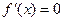 ,解得
,解得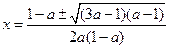
则当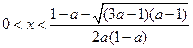 或
或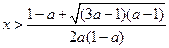 时,
时,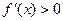
当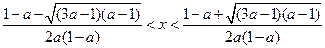 时,
时,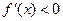
则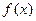 在
在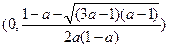 ,
,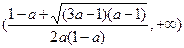 上单调递增,
上单调递增,
在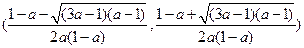 上单调递减
上单调递减
② 当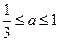 时,
时,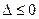 ,
,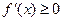 ,则
,则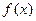 在
在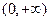 上单调递增
上单调递增
③ 当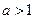 时,
时,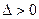 ,令
,令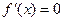 ,解得
,解得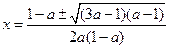
∵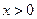 ,∴
,∴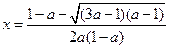
则当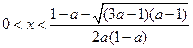 时,
时,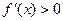
当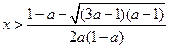 时,
时,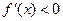
则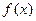 在
在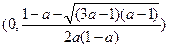 上单调递增,在
上单调递增,在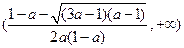 上单调递减
上单调递减
20.(本小题满分14分)
设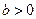 ,数列
,数列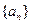 满足
满足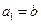 ,
,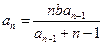
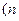 ≥
≥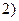 .
.
(1)求数列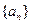 的通项公式;
的通项公式;
(2)证明:对于一切正整数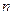 ,
,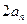 ≤
≤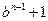 .
.
20.(1)解:∵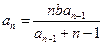
∴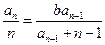
∴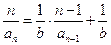
① 当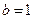 时,
时,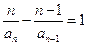 ,则
,则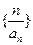 是以1为首项,1为公差的等差数列
是以1为首项,1为公差的等差数列
∴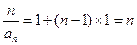 ,即
,即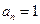
② 当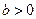 且
且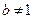 时,
时,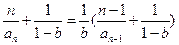
当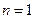 时,
时,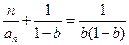
∴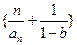 是以
是以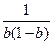 为首项,
为首项,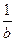 为公比的等比数列
为公比的等比数列
∴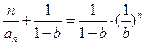
∴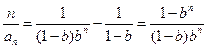
∴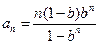
综上所述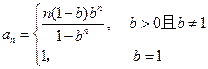
(2)证明:① 当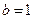 时,
时,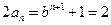 ;
;
② 当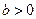 且
且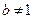 时,
时,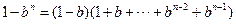
要证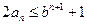 ,只需证
,只需证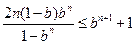 ,
,
即证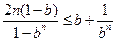
即证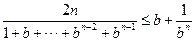
即证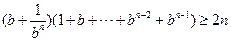
即证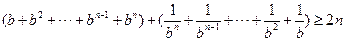
∵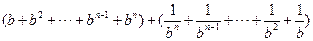
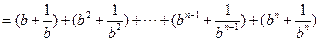
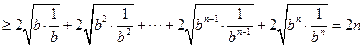 ,∴原不等式成立
,∴原不等式成立
∴对于一切正整数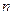 ,
,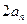 ≤
≤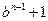 .
.
21.(本小题满分14分)
在平面直角坐标系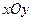 上,直线
上,直线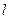 :
: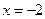 交
交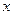 轴于点
轴于点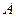 .设
.设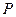 是
是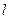 上一点,
上一点,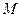 是线段
是线段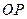 的垂直平分线上一点,且满足
的垂直平分线上一点,且满足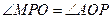 .
.
(1)当点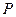 在
在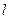 上运动时,求点
上运动时,求点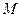 的轨迹
的轨迹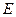 的方程;
的方程;
(2)已知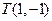 ,设
,设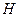 是
是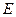 上动点,求
上动点,求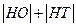 的最小值,并给出此时点
的最小值,并给出此时点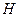 的坐标;
的坐标;
(3)过点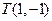 且不平行于
且不平行于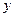 轴的直线
轴的直线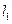 与轨迹
与轨迹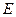 有且只有两个不同的交点,求直线
有且只有两个不同的交点,求直线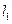 的斜率
的斜率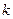 的取值范围.
的取值范围.
21.解:(1)如图所示,连接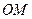 ,则
,则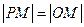
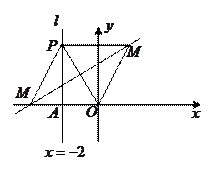
∵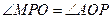 ,
,
∴动点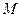 满足
满足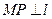 或
或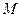 在
在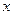 的负半轴上,设
的负半轴上,设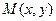
① 当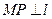 时,
时,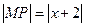 ,
,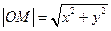
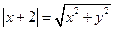 ,化简得
,化简得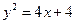
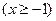
② 当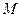 在
在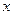 的负半轴上时,
的负半轴上时,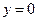
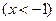
综上所述,点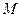 的轨迹
的轨迹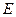 的方程为
的方程为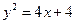
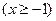 或
或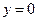
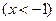
(2)由(1)知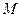 的轨迹是顶点为
的轨迹是顶点为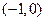 ,焦点为原点的抛物线和
,焦点为原点的抛物线和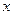 的负半轴
的负半轴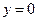
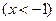
① 若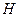 是抛物线上的动点,过
是抛物线上的动点,过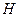 作
作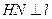 于
于
由于 是抛物线
是抛物线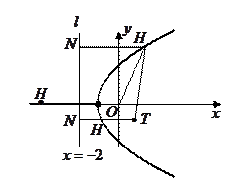 的准线,根据抛物线的定义有
的准线,根据抛物线的定义有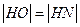
则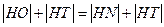
当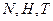 三点共线时,
三点共线时,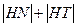 有最小值
有最小值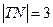
求得此时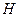 的坐标为
的坐标为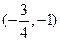
② 若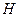 是
是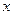 的负半轴
的负半轴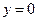
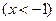 上的动点
上的动点
显然有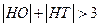
综上所述,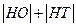 的最小值为3,此时点
的最小值为3,此时点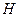 的坐标为
的坐标为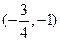
(3)如图,设抛物线顶点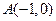 ,则直线
,则直线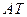 的斜率
的斜率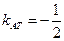
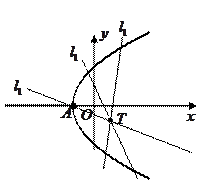
∵点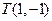 在抛物线内部,
在抛物线内部,
∴过点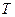 且不平行于
且不平行于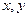 轴的直线
轴的直线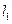 必与抛物线有两个交点
必与抛物线有两个交点
则直线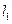 与轨迹
与轨迹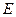 的交点个数分以下四种情况讨论:
的交点个数分以下四种情况讨论:
① 当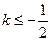 时,直线
时,直线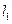 与轨迹
与轨迹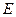 有且只有两个不同的交点
有且只有两个不同的交点
② 当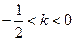 时,直线
时,直线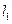 与轨迹
与轨迹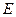 有且只有三个不同的交点
有且只有三个不同的交点
③ 当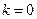 时,直线
时,直线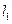 与轨迹
与轨迹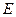 有且只有一个交点
有且只有一个交点
④ 当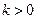 时,直线
时,直线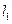 与轨迹
与轨迹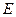 有且只有两个不同的交点
有且只有两个不同的交点
综上所述,直线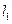 的斜率
的斜率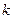 的取值范围是
的取值范围是