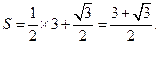(二)填空题:把答案填在答题卡相应题号后的横线上( 本大题共5小题,每小题5分,共25分)
11.设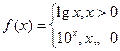 ,则
,则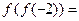 ______.
______.
【分析】由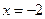 算起,先判断
算起,先判断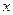 的范围,是大于0,还是不大于0,;再判断
的范围,是大于0,还是不大于0,;再判断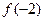 作为自变量的值时的范围,最后即可计算出结果.
作为自变量的值时的范围,最后即可计算出结果.
【解】∵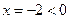 ,∴
,∴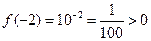 ,所以
,所以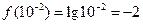 ,即
,即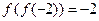 .
.
【答案】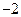
12.如图,点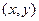 在四边形ABCD内部和边界上运动,那么
在四边形ABCD内部和边界上运动,那么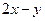 的最小值为________.
的最小值为________.
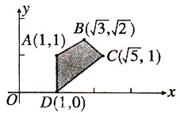
【分析】本题为线性规划问题,采用数形结合法解答,解答本题的关键是确定目标函数过哪一个点时取得最小值.
【解】目标函数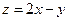 ,当
,当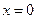 时,
时,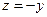 ,所以当
,所以当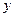 取得最大值时,
取得最大值时,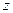 的值最小;移动直线
的值最小;移动直线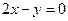 ,当直线移动到过点A时,
,当直线移动到过点A时,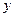 最大,即
最大,即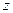 的值最小,此时
的值最小,此时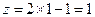 .
.
【答案】1
13.观察下列等式
1=1
2+3+4=9
3+4+5+6+7=25
4+5+6+7+8+9+10=49
照此规律,第五个等式应为__________________.
【分析】归纳总结时,看等号左边是子的变化规律,右边结果的特点,根据以上规律写出第五个等式,注意行数、项数及其变化规律是解答本题的关键.
【解】把已知等式与行数对应起来,则每一个等式的左边的式子的第一个数是行数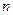 ,加数的个数是
,加数的个数是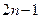 ;等式右边都是完全平方数,行数 等号左边的项数
;等式右边都是完全平方数,行数 等号左边的项数
1=1 1 1
2+3+4=9 2 3
3+4+5+6+7=25 3 5
4+5+6+7+8+9+10=49 4 7
则第5行等号的左边有9项,右边是9的平方,所以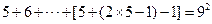 ,
,
即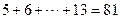 .
.
【答案】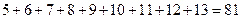 (或
(或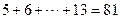 )
)
14.设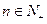 ,一元二次方程
,一元二次方程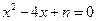 有整数根的充要条件是
有整数根的充要条件是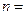 .
.
【分析】直接利用求根公式进行计算,然后用完全平方数、整除等进行判断计算.
【解】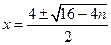
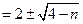 ,因为
,因为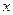 是整数,即
是整数,即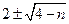 为整数,所以
为整数,所以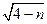 为整数,且
为整数,且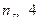 ,又因为
,又因为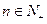 ,取
,取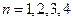 验证可知
验证可知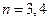 符合题意;反之
符合题意;反之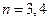 时,可推出一元二次方程
时,可推出一元二次方程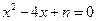 有整数根.
有整数根.
【答案】3或4
15.(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)
A.(不等式选做题)若不等式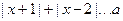 对任意
对任意 R恒成立,则
R恒成立,则 的取值范围是 .
的取值范围是 .
【分析】先确定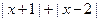 的取值范围,则只要
的取值范围,则只要 不大于
不大于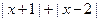 的最小值即可.
的最小值即可.
【解】当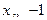 时,
时,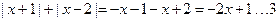 ;
;
当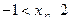 时,
时,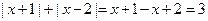 ;
;
当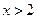 时,
时,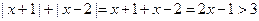 ;
;
综上可得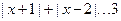 ,所以只要
,所以只要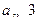 ,
,
即实数 的取值范围是
的取值范围是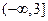 .
.
【答案】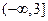
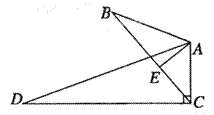
B.(几何证明选做题)如图,∠B=∠D,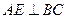 ,
,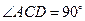 ,且AB=6,AC=4,AD=12,则AE= .
,且AB=6,AC=4,AD=12,则AE= .
【分析】寻找两个三角形相似的条件,再根据相似三角形的对应边成比例求解.
【解】因为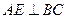 ,
,
所以∠AEB=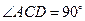 ,又因为∠B=∠D,所以△AEB∽△ACD,所以
,又因为∠B=∠D,所以△AEB∽△ACD,所以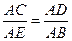 ,所以
,所以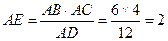 .
.
【答案】2
C.(坐标系与参数方程选做题)直角坐标系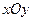 中,以原点O为极点,
中,以原点O为极点,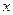 轴的正半轴为极轴建立极坐标系,设点A,B分别在曲线
轴的正半轴为极轴建立极坐标系,设点A,B分别在曲线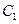 :
: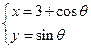 (
(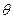 为参数)和曲线
为参数)和曲线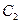 :
: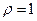 上,则
上,则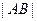 的最小值为 .
的最小值为 .
【分析】利用化归思想和数形结合法,把两条曲线转化为直角坐标系下的方程.
【解】曲线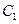 的方程是
的方程是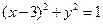 ,曲线
,曲线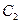 的方程是
的方程是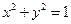 ,两圆外离,所以
,两圆外离,所以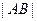 的最小值为
的最小值为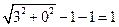 .
.
【答案】1
(3)解答题:接答应写出文字说明、证明过程或演算步骤(本大题共6小题,共75分)
P.(本小题满分12分)
如图,在△ABC中,∠ABC=45°,∠BAC=90°,AD是BC上的高,沿AD把△ABD折起,使∠BDC=90°。
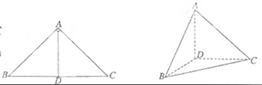
(1)证明:平面ADB⊥平面BDC;
(2 )设BD=1,求三棱锥D—ABC的表面积。
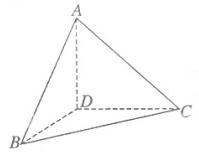
【分析】(1)确定图形在折起前后的不变性质,如角的大小不变,线段长度不变,线线关系不变,再由面面垂直的判定定理进行推理证明;(2)充分利用垂直所得的直角三角形,根据直角三角形的面积公式计算.
【解】(1)∵折起前AD是BC边上的高,
∴ 当Δ ABD折起后,AD⊥DC,AD⊥DB,
又DB DC=D,
DC=D,
∴AD⊥平面BDC,又∵AD 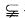 平面BDC.
平面BDC.
∴平面ABD⊥平面BDC.
(2)由(1)知,DA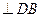 ,
,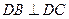 ,
,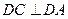 ,
,
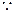 DB=DA=DC=1,
DB=DA=DC=1,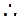 AB=BC=CA=
AB=BC=CA=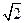 ,
,
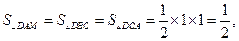
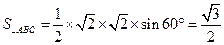
∴三棱锥D—ABC的表面积是