一、选择题:在每小题给出的四个选项中,只有一项符合题目要求(本大题共10小题,每小题5分,共50分)
1. 集合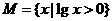 ,
,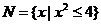 ,则
,则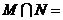 ( C )
( C )
A 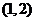 B
B 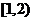 C
C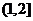 D
D 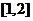
解析: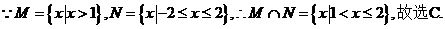
答案:C
点评:本题主要考察集合的运算以及不等式的解法.
2.下列函数中,既是奇函数又是增函数的为( )
A 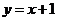 B
B 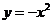 C
C 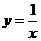 D
D 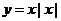
解析:A是增函数,不是奇函数;B和C都不是定义域内的增函数,排除,只有D正确,因此选D.
答案:D
点评:该题主要考察函数的奇偶性和单调性,理解和掌握基本函数的性质是关键.
3. 对某商店一个月内每天的顾客人数进行了统计,得到样本的茎叶图(如图所示),则该样本的中位数、众数、极差分别是 ( A )

A.46,45,56 B.46,45,53
C.47,45,56 D.45,47,53
解析:由概念知中位数是中间两数的平均数,即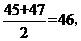 众数是45,极差为68-12=56.所以选A.
众数是45,极差为68-12=56.所以选A.
答案:A
点评:此题主要考察样本数据特征的概念,要正确地理解样本数据特征的概念以及正确地用来估计总体.
4.设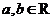 ,
,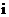 是虚数单位,则“
是虚数单位,则“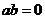 ”是“复数
”是“复数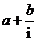 为纯虚数”的( B )
为纯虚数”的( B )
A.充分不必要条件 B。必要不充分条件
C 。充分必要条件 D。既不充分也不必要条件
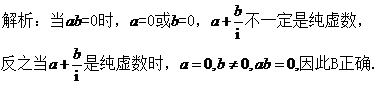
答案:B
点评:此题主要考察充分必要条件和复数的概念以及它们之间的逻辑关系,掌握概念是根本.
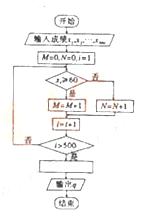
5. 下图是计算某年级500名学生期末考试(满分为100分)及格率q的程序框图,则图中空白框内应填入( )
A. q=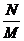 B 。q=
B 。q=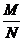
C.q=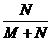 D.q=
D.q=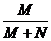
解析:因为执行判断框“是”计算的及格的总分数M,“否”统计的是不及格的成绩,所以及格率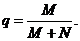 选D.
选D.
答案:D
点评:本题主要考察算法中的循环结构,算法的功能以及算法的基本思想,对算法的学习和把握要全面深入.
6. 已知圆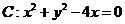 ,
,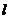 过点
过点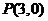 的直线,则( )
的直线,则( )
A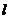 与
与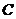 相交 B
相交 B 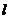 与
与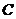 相切 C
相切 C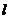 与
与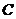 相离 D. 以上三个选项均有可能
相离 D. 以上三个选项均有可能
解析:因为点P(3,0)在圆的内部,所以过点P的直线必与圆相交.选A.
答案:A
点评:该题主要考察直线和元的位置关系,掌握点和圆、直线和圆的位置关系是关键.
7.设向量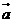 =(1.
=(1.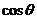 )与
)与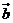 =(-1, 2
=(-1, 2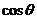 )垂直,则
)垂直,则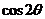 等于 ( C )
等于 ( C )
A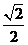 B
B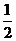 C .0 D.-1
C .0 D.-1
解析: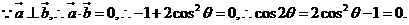 正确的是C.
正确的是C.
答案:C
点评:此题主要考察平面向量的数量积的概念、运算和性质,同时考察三角函数的求值运算.
8. 将正方形(如图1所示)截去两个三棱锥,得到图2所示的几何体,则该几何体的左视图为 ( B )
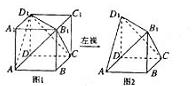
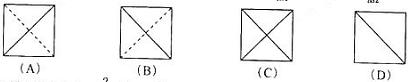
解析:因为从左面垂直光线在竖直平面上的正投影是正方形,其中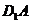 的正投影是正方形的对角线(实线),
的正投影是正方形的对角线(实线),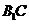 的正投影被遮住是虚线,所以B正确.
的正投影被遮住是虚线,所以B正确.
答案:B
点评:本题主要考察空间图像的直观图与三视图,考察空间想象能力与逻辑推理能力,注意培养.
9. 设函数f(x)=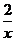 +lnx 则 ( D )
+lnx 则 ( D )
A.x=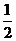 为f(x)的极大值点 B.x=
为f(x)的极大值点 B.x=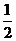 为f(x)的极小值点
为f(x)的极小值点
C.x=2为 f(x)的极大值点 D.x=2为 f(x)的极小值点

答案:D
点评:本题主要考察利用导数求函数的极值点,是导数在函数中的基本应用.
10. 小王从甲地到乙地的时速分别为a和b(a<b),其全程的平均时速为v,则 ( A )
A.a<v<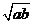 B.v=
B.v=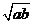 C.
C. 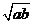 <v<
<v<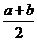 D.v=
D.v=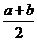
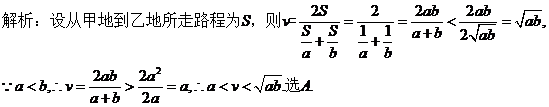
答案:A.
点评:本题主要考察基本不等式及其应用,其中正确列式巧妙运用均值不等式是关键,同时也要注意题设条件.












