第Ⅰ卷
一、选择题
(1)复数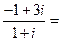
(A)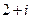 (B)
(B)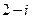 (C)
(C)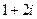 (D)
(D)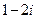
(2)已知集合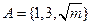 ,
,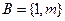 ,
,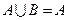 ,则
,则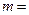
(A)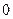 或
或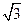 (B)
(B)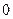 或
或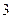 (C)
(C)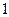 或
或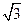 (D)
(D)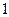 或
或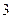
(3)椭圆的中心在原点,焦距为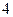 ,一条准线为
,一条准线为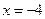 ,则该椭圆的方程为
,则该椭圆的方程为
(A)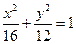 (B)
(B)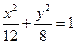 (C)
(C)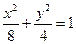 (D)
(D)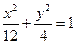
(4)已知正四棱柱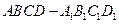 中 ,
中 ,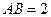 ,
,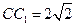 ,
,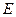 为
为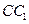 的中点,则直线
的中点,则直线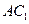 与平面
与平面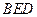 的距离为
的距离为
(A)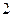 (B)
(B)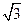 (C)
(C)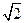 (D)
(D)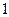
(5)已知等差数列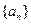 的前
的前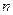 项和为
项和为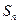 ,
,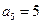 ,
,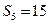 ,则数列
,则数列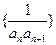 的前
的前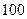 项和为
项和为
(A)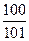 (B)
(B)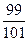 (C)
(C)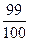 (D)
(D)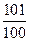
(6)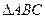 中,
中,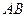 边的高为
边的高为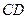 ,若
,若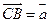 ,
,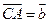 ,
,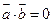 ,
,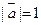 ,
,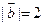 ,则
,则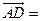
(A)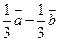 (B)
(B)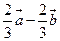 (C)
(C)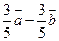 (D)
(D)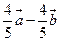
(7)已知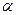 为第二象限角,
为第二象限角,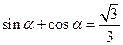 ,则
,则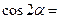
(A)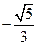 (B)
(B)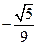 (C)
(C)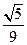 (D)
(D)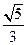
(8)已知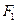 、
、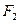 为双曲线
为双曲线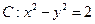 的左、右焦点,点
的左、右焦点,点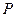 在
在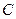 上,
上,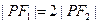 ,则
,则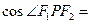
(A)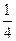 (B)
(B)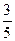 (C)
(C)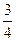 (D)
(D)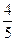
(9)已知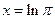 ,
,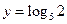 ,
,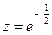 ,则
,则
(A)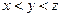 (B)
(B)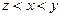 (C)
(C)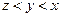 (D)
(D)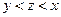
(10)已知函数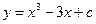 的图像与
的图像与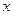 恰有两个公共点,则
恰有两个公共点,则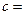
(A)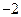 或
或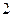 (B)
(B)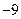 或
或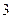 (C)
(C)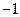 或
或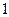 (D)
(D)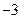 或
或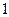
(11)将字母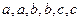 排成三行两列,要求每行的字母互不相同,每列的字母也互不相同,则不同的排列方法共有
排成三行两列,要求每行的字母互不相同,每列的字母也互不相同,则不同的排列方法共有
(A)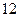 种 (B)
种 (B)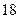 种 (C)
种 (C)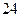 种 (D)
种 (D)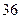 种
种
(12)正方形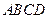 的边长为
的边长为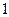 ,点
,点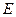 在边
在边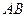 上,点
上,点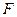 在边
在边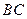 上,
上,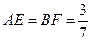 。动点
。动点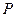 从
从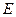 出发沿直线向
出发沿直线向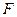 运动,每当碰到正方形的边时反弹,反弹时反射角等于入射角,当点
运动,每当碰到正方形的边时反弹,反弹时反射角等于入射角,当点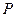 第一次碰到
第一次碰到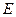 时,
时,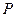 与正方形的边碰撞的次数为
与正方形的边碰撞的次数为
(A)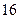 (B)
(B)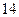 (C)
(C)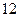 (D)
(D)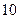
第Ⅱ卷
二。填空题:本大题共4小题,每小题5分,共20分,把答案填在题中横线上。
(注意:在试题卷上作答无效)
(13)若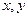 满足约束条件
满足约束条件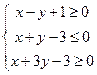 ,则
,则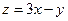 的最小值为__________。
的最小值为__________。
(14)当函数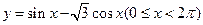 取得最大值时,
取得最大值时,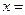 ___________。
___________。
(15)若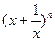 的展开式中第
的展开式中第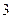 项与第
项与第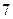 项的二项式系数相等,则该展开式中
项的二项式系数相等,则该展开式中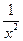 的系数为_________。
的系数为_________。
(16)三棱柱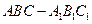 中,底面边长和侧棱长都相等,
中,底面边长和侧棱长都相等,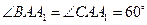 ,则异面直线
,则异面直线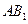 与
与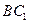 所成角的余弦值为____________。
所成角的余弦值为____________。
三.解答题:本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤。
(17)(本小题满分10分)(注意:在试卷上作答无效)
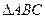 的内角
的内角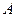 、
、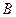 、
、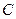 的对边分别为
的对边分别为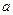 、
、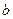 、
、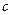 ,已知
,已知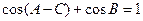 ,
,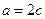 ,求
,求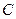 。
。
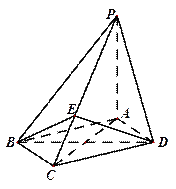
(18)(本小题满分12分)(注意:在试题卷上作答无效)
如图,四棱锥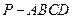 中,底面
中,底面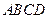 为菱形,
为菱形,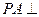 底面
底面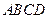 ,
,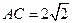 ,
,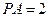 ,
,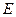 是
是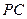 上的一点,
上的一点,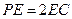 。
。
(Ⅰ)证明: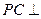 平面
平面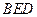 ;
;
(Ⅱ)设二面角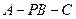 为
为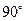 ,求
,求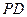 与平面
与平面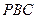 所成角的大小。
所成角的大小。
(19)(本小题满分12分)(注意:在试题卷上作答无效)
乒乓球比赛规则规定:一局比赛,双方比分在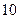 平前,一方连续发球
平前,一方连续发球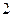 次后,对方再连续发球
次后,对方再连续发球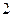 次,依次轮换。每次发球,胜方得
次,依次轮换。每次发球,胜方得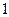 分,负方得
分,负方得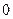 分。设在甲、乙的比赛中,每次发球,发球方得
分。设在甲、乙的比赛中,每次发球,发球方得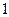 分的概率为
分的概率为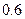 ,各次发球的胜负结果相互独立。甲、乙的一局比赛中,甲先发球。
,各次发球的胜负结果相互独立。甲、乙的一局比赛中,甲先发球。
(Ⅰ)求开始第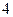 次发球时,甲、乙的比分为
次发球时,甲、乙的比分为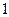 比
比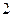 的概率;
的概率;
(Ⅱ)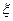 表示开始第
表示开始第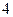 次发球时乙的得分,求
次发球时乙的得分,求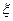 的期望。
的期望。
(20)(本小题满分12分)(注意:在试题卷上作答无效)
设函数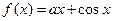 ,
,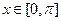 。
。
(Ⅰ)讨论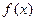 的单调性;
的单调性;
(Ⅱ)设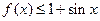 ,求
,求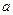 的取值范围。
的取值范围。
(21)(本小题满分12分)(注意:在试卷上作答无效)
已知抛物线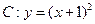 与圆
与圆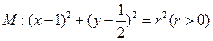 有一个公共点
有一个公共点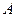 ,且在点
,且在点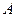 处两曲线的切线为同一直线
处两曲线的切线为同一直线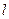 .
.
(Ⅰ)求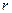 ;
;
(Ⅱ)设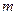 、
、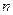 是异于
是异于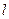 且与
且与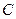 及
及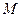 都相切的两条直线,
都相切的两条直线,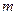 、
、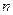 的交点为
的交点为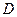 ,求
,求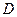 到
到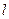 的距离。
的距离。
(22)(本小题满分12分)(注意:在试卷上作答无效)
函数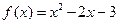 ,定义数列
,定义数列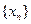 如下:
如下: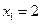 ,
,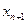 是过两点
是过两点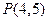 、
、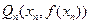 的直线
的直线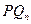 与
与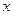 轴交点的横坐标。
轴交点的横坐标。
(Ⅰ)证明: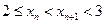 ;
;
(Ⅱ)求数列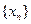 的通项公式。
的通项公式。












