一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项符合题目要求的.
1. 复数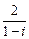 等于
等于
A.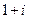 B.
B. 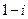 C.
C. 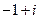 D.
D. 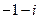

2. 下列命题中的假命题是
A. 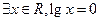 B.
B. 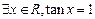
C. 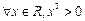 D.
D. 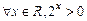
2.答案C
【命题意图】本题考查了含有存在量词与全称量词的命题的真假判定。
【解析】当x=1时,lgx=0,即A正确;当x=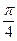 时,tanx=1,即B正确;当x≤0时,x3>0不成立,即C错误;对于任意的x∈R,都有2x>0,即D正确;故选C;
时,tanx=1,即B正确;当x≤0时,x3>0不成立,即C错误;对于任意的x∈R,都有2x>0,即D正确;故选C;
3. 某商品销售量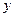 (件)与销售价格
(件)与销售价格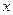 (元/件)负相关,则其回归方程可能是
(元/件)负相关,则其回归方程可能是
A. 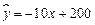 B.
B. 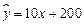
C. 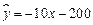 D.
D. 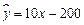
3.答案A
【命题意图】本题考查了线性回归方程及其实际应用问题。
【解析】由于某商品销售量y与销售价格x负相关,则b<0,排除选项B和D,而根据特殊值x=2,可以排除选项C,故选A;
4. 极坐标方程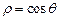 和参数方程
和参数方程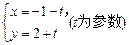 所表示的图形分别是
所表示的图形分别是
A. 直线、直线 B. 直线、圆 C. 圆、 圆 D. 圆、直线
圆 D. 圆、直线
 5. 设抛物线
5. 设抛物线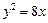 上一点P到
上一点P到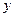 轴的距离是4,则点P到该抛物线焦点的距离是
轴的距离是4,则点P到该抛物线焦点的距离是
A. 4 B. 6 C. 8 D. 12
5.答案B
【命题意图】本题考查了抛物 线的定义及其应用。
线的定义及其应用。
【解析】由抛物线y2=8x知p=4,而其上一点P到y轴的距离为4,则点P到准线x=-2的距离6,根据抛物线的定义知点P到焦点的距离也为6,故选B;
6. 若非零向量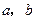 满足|
满足|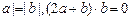 ,则
,则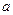 与
与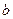 的夹角为
的夹角为
A.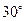 B.
B. 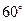 C.
C. 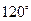
 D.
D. 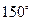
6.答案C
【命题意图】本题考查了平面向量的数量积、夹角等相关概念。
【解析】设|a|=|b|=m,a与b夹角为θ,由于(2a+b)•b=2a•b+b2=2m2cosθ+m2=0,则有cosθ=-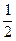 ,那么θ=120º,故选C;
,那么θ=120º,故选C;
7.在△ABC中,角A,B,C所对的边长分别为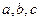 ,若∠C=1
,若∠C=1 20°,c=
20°,c=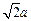 ,则
,则
A. 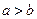 B.
B. 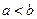
C. 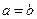 D.
D. 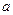 与
与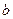 的大小关系不能确定
的大小关系不能确定

8.函数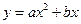
 与
与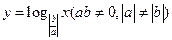 在同一直角坐标系中的图像可能是
在同一直角坐标系中的图像可能是
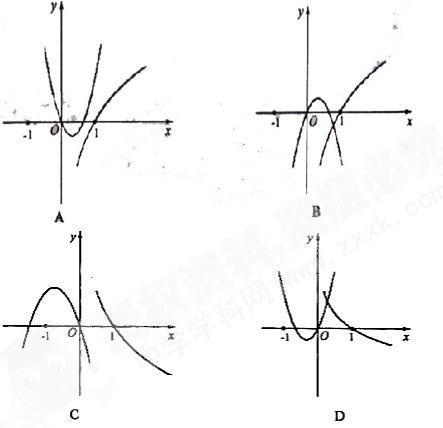
8.答案D
【命题意图】本题考查了二次函数与对数函数的图象问题,关键是分类讨论与探究性问题的分析与应用。
【解析】对于函数y=ax2+bx与函数y=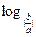 x,当|
x,当|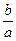 |>1时,函数y=
|>1时,函数y=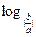 x在定义域内是增函数,对应的图象可能是选项A和B,此时y=ax(x+
x在定义域内是增函数,对应的图象可能是选项A和B,此时y=ax(x+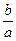 ),即二次函数除过原点外的另一个与x轴的交点应该在|
),即二次函数除过原点外的另一个与x轴的交点应该在|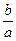 |>1外,选项A和B都不满足;当|
|>1外,选项A和B都不满足;当|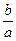 |<1时,函数y=
|<1时,函数y=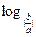 x在定义域内是减函数,对应的图象可能是选项C和D,此时y=ax(x+
x在定义域内是减函数,对应的图象可能是选项C和D,此时y=ax(x+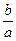 ),即二次函数除过原点外的另一个与x轴的交点应该在|
),即二次函数除过原点外的另一个与x轴的交点应该在|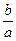 |<1外,选项C不满足;故选D;
|<1外,选项C不满足;故选D;
二、填空题:本大题共7小题,每小题5分,共35分,把答案填在答题卡中对应题号后的横线上.
9.已知集合A={1,2,3,},B={2,m,4},A∩B={2,3},则m=
9.答案3
【命题意图】本题考查了集合的运算与参数的求解
【解析】由于A={1,2,3},B={2,m,4},而A∩B={2,3},那么3∈B,则m=3,故填3;
10. 已知一种材料的最佳加入量在110g到21 0g之间.若用0.618法安排实验,则第一次试点的加入量可以是 g.
0g之间.若用0.618法安排实验,则第一次试点的加入量可以是 g.
10.答案161.8或138.2
【命题意图】本题考查了试验方法的分析与应用。
【解析】根据0.618法的特点,在最佳加入量在100g到200g之间时,第一次试点的加入量应该是:100+0.618×100=161.8或200-0.618×100=138.2,故填161.8或138.2;
11.在区间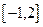 上随即取一个数
上随即取一个数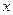 ,则
,则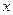 ∈[0,1]的概率为 .
∈[0,1]的概率为 .
11.答案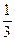
【命题意图】本题考查了几何概型的概率求解。
【解析】由于区间[-1,2]的长度为3,而[0,1]的长度为1,那么所求的概率为P=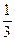 ,故选
,故选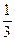 ;
;
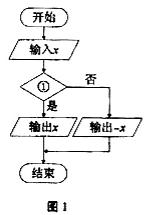
12.图1是求实数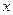 的绝对值的算法程序框图,则判断框①中可填 .
的绝对值的算法程序框图,则判断框①中可填 .
12.答案“x>0”或“x>0?”或“x≥0”或“x≥0?”(这些答案都可以,只要填一个即可)【命题意图】本题考查了算法的程序框的识别与应用。
【解析】由于算法程序框图是求实数x的绝对值,在“是”的情况下执行“输出x”,在“否”的情况下执行“输出-x”,那么判断框①中可填的可以是:“x>0”或“x>0?”或“x≥0”或“x≥0?”,故填“x>0”或“x>0?”或“x≥0”或“x≥0?”;
13.图2中的三个直角三角形是一个体积为20cm2的几何体的三视图,则h= 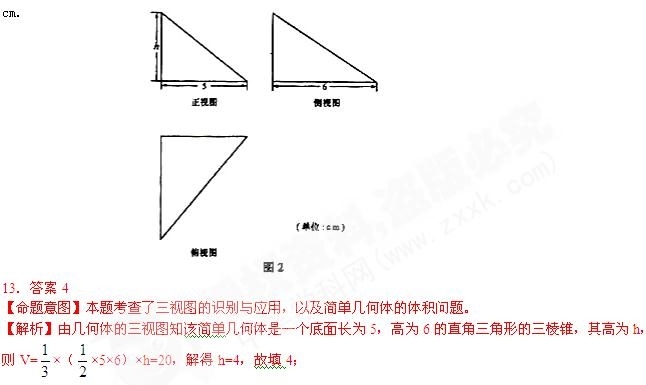
14.若不同两点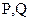 的坐标分别为
的坐标分别为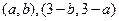 ,则线段PQ的垂直平分线
,则线段PQ的垂直平分线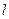 的斜率为
的斜率为
;圆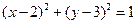 关于直线
关于直线
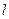 对称的圆的方程为 .
对称的圆的方程为 .
14.答案-1,x2+(y-1)2=1
【命题意图】本题考查了两点间的距离公式、直线方程、斜率公式与两直线的位置关系,圆的方程与性质、对称问题等。
【解析】由条件知线段PQ的垂直平分线l的方程为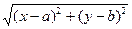 =
=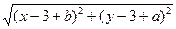 ,整理可得x+y-3=0,由于y=-x+3,则直线l的斜率为k=-1;圆(x-2)2+(y-3)2=1的圆心(2,3)关于直线l:x+y-3=0的对称点为(0,1),则对称的圆的方程为x2+(y-1)2=1,故填-1,x2+(y-1)2=1;
,整理可得x+y-3=0,由于y=-x+3,则直线l的斜率为k=-1;圆(x-2)2+(y-3)2=1的圆心(2,3)关于直线l:x+y-3=0的对称点为(0,1),则对称的圆的方程为x2+(y-1)2=1,故填-1,x2+(y-1)2=1;
15.若规定
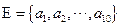 的子集
的子集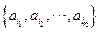 为E的第k个子集,其中
为E的第k个子集,其中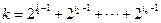 ,则
,则
(1)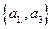 是E的第____个子集;
是E的第____个子集;
(2)E的第211个子集是_______.
15.答案5;{a1,a2,a5,a7,a8}
【命题意图】本题考查了集合的创新应用问题,关键是集合中的相关概念问题与推理分析能力的应用,以及对应的配凑思维。
【解析】根据规定,{a1,a3}是E的子集位数为k=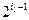 +
+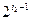 =
=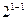 +
+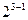 =1+4=5;而要求E的第211个子集,根据规定,
=1+4=5;而要求E的第211个子集,根据规定,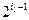 +
+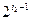 +…+
+…+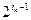 =211=128+64+16+2+1=
=211=128+64+16+2+1=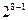 +
+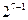 +
+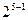 +
+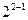 +
+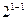 ,即对应的子集为{a1,a2,a5,a7,a8},故填5,{a1,a2,a5,a7,a8};
,即对应的子集为{a1,a2,a5,a7,a8},故填5,{a1,a2,a5,a7,a8};












