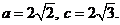第Ⅱ卷
二.填空题:本大题共4小题,每小题4分,共16分。请把答案填在答题卡上
13.已知向量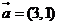 ,
,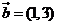 ,
,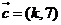 ,若
,若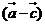 ∥
∥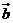 ,则
,则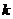 =__________.
=__________.
答案: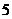
【解析】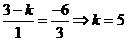
14.正三棱柱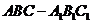 内接于半径为
内接于半径为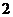 的球,若
的球,若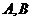 两点的球面距离为
两点的球面距离为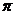 ,则正三棱柱的体积为 .
,则正三棱柱的体积为 .
答案: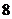
【解析】由条件可得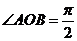 ,所以
,所以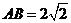 ,
,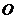 到平面
到平面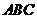 的距离为
的距离为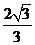 ,所以所求体积等于
,所以所求体积等于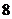 .
.
15.若不等式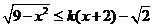 的解集为区间
的解集为区间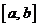 ,且
,且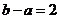 ,则
,则 .
.
答案: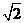
【解析】由数形结合,直线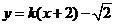 在半圆
在半圆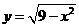 之下必须
之下必须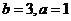 ,则直线
,则直线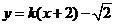 过点(
过点(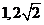 ),则
),则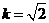
16.设直线系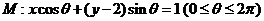 ,对于下列四个命题:
,对于下列四个命题:
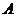 .
.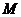 中所有直线均经过一个定点
中所有直线均经过一个定点
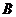 .存在定点
.存在定点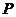 不在
不在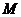 中的任一条直线上
中的任一条直线上
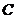 .对于任意整数
.对于任意整数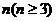 ,存在正
,存在正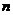 边形,其所有边均在
边形,其所有边均在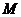 中的直线上
中的直线上
 .
. 中的直线所能围成的正三角形面积都相等
中的直线所能围成的正三角形面积都相等
其中真命题的代号是 (写出所有真命题的代号).
答案: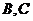
【解析】因为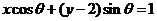 所以点
所以点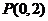 到
到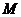 中每条直线的距离
中每条直线的距离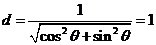
即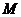 为圆
为圆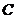 :
: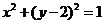 的全体切线组成的集合,从而
的全体切线组成的集合,从而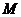 中存在两条平行直线,所以A错误
中存在两条平行直线,所以A错误
又因为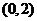 点不存在任何直线上,所以B正确
点不存在任何直线上,所以B正确
对任意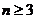 ,存在正
,存在正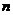 边形使其内切圆为圆
边形使其内切圆为圆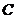 ,故
,故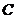 正确
正确
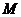 中边能组成两个大小不同的正三角形
中边能组成两个大小不同的正三角形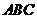 和
和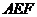 ,故D错误,
,故D错误,
故命题中正确的序号是 B,C
三.解答题:本大题共6小题,共74分。解答应写出文字说明,证明过程或演算步骤
17.(本小题满分12分)
设函数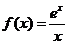
(1)求函数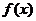 的单调区间;
的单调区间;
(2)若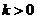 ,求不等式
,求不等式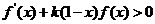 的解集.
的解集.
解: (1) 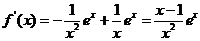 , 由
, 由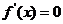 ,得
,得 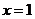 .
.
因为 当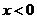 时,
时,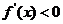 ; 当
; 当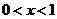 时,
时,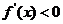 ; 当
; 当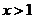 时,
时,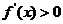 ;
;
所以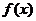 的单调增区间是:
的单调增区间是: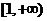 ; 单调减区间是:
; 单调减区间是: 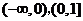 .
.
(2) 由 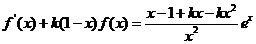
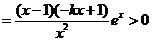 ,
,
得: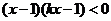 .
.
故:当 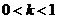 时, 解集是:
时, 解集是: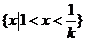 ;
;
当  时,解集是:
时,解集是:  ;
;
当  时, 解集是:
时, 解集是: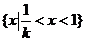 .
.
18.(本小题满分12分)
某公司拟资助三位大学生自主创业,现聘请两位专家,独立地对每位大学生的创业方案进行评审.假设评审结果为“支持”或“不支持”的概率都是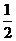 .若某人获得两个“支持”,则给予10万元的创业资助;若只获得一个“支持”,则给予5万元的资助;若未获得“支持”,则不予资助,令
.若某人获得两个“支持”,则给予10万元的创业资助;若只获得一个“支持”,则给予5万元的资助;若未获得“支持”,则不予资助,令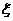 表示该公司的资助总额.
表示该公司的资助总额.
(1) 写出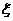 的分布列; (2) 求数学期望
的分布列; (2) 求数学期望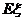
解:(1)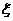 的所有取值为
的所有取值为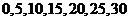
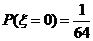
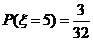
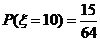
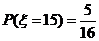
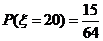
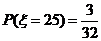
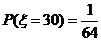
(2)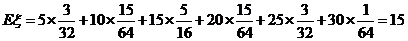 .
.
19.(本小题满分12分)
△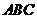 中,
中,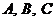 所对的边分别为
所对的边分别为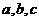 ,
,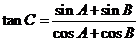 ,
,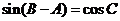 .
.
(1)求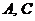 ;
;
(2)若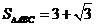 ,求
,求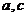 .
. 
解:(1) 因为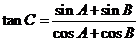 ,即
,即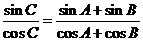 ,
,
所以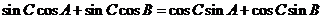 ,
,
即 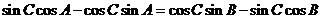 ,
,
得 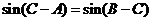 . 所以
. 所以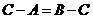 ,或
,或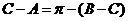 (不成立).
(不成立).
即 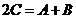 , 得
, 得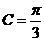 ,所以.
,所以.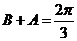
又因为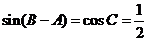 ,则
,则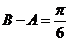 ,或
,或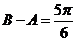 (舍去)
(舍去)
得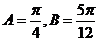
(2)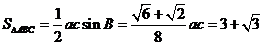 ,
,
又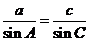 , 即
, 即 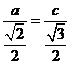 ,
,
得