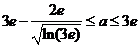(20)(本题满分15分)如图,在三棱锥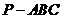 中,
中,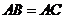 ,D为BC的中点,PO⊥平面ABC,垂足O落在线段AD上,已知BC=8,PO=4,AO=3,OD=2
,D为BC的中点,PO⊥平面ABC,垂足O落在线段AD上,已知BC=8,PO=4,AO=3,OD=2
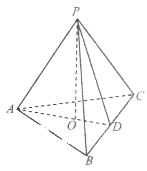
Ⅰ)证明:AP⊥BC;(Ⅱ)在线段AP上是否存在点M,
使得二面角A-MC-β为直二面 角?若存在,求出AM的长;若不存在,请说明理由。
角?若存在,求出AM的长;若不存在,请说明理由。
【解析】:本题主要考查空间点、线、面位置关系,二面角等基础知识,空间向量的应用,同时考查空间想象能力和运算求解能力。满分15分
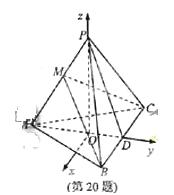
法一:(Ⅰ)证明:如图,以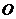 为原点,以射线
为原点,以射线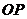 为
为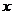 轴的正半轴,建立空间直角坐标系
轴的正半轴,建立空间直角坐标系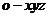 ,则
,则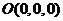 ,
,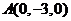 ,
,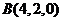 ,
,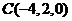 ,
,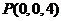 ,
,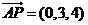 ,
,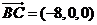 由此可得
由此可得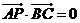 ,所以
,所以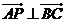 ,即
,即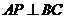
(Ⅱ)解:设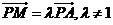 ,则
,则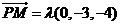 ,
,
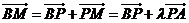
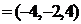
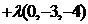
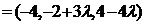 ,
,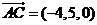 ,
,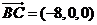
设平面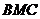 的法向量
的法向量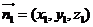 ,
,

综上所述,存在点M 符合题意,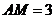
法二(Ⅰ)证明: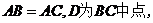
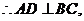
又
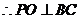 因为
因为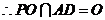 所以
所以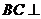 平面
平面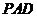 故
故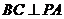
(Ⅱ)如图,在平面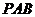 内作
内作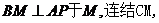
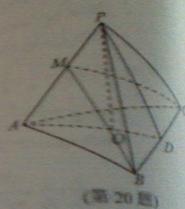
由(Ⅰ)知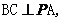 得
得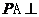 平面
平面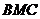 ,
,
又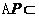 平面
平面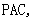 所以平面
所以平面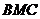
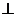 平面
平面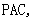
在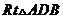 中,
中,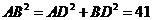 得
得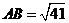
在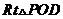 中,
中,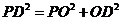 ,
,
在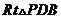 中,
中,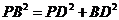 所以
所以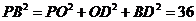 得
得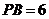 ,
,
在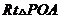 中,
中,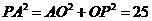 得
得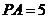 又
又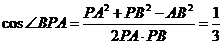
从而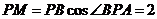 ,所以
,所以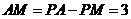 综上所述,存在点M 符合题意,
综上所述,存在点M 符合题意,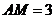
(21)(本题满分15分)已知抛物线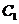 :
: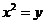 ,圆
,圆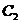 :
: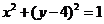 的圆心为点M(Ⅰ)求点M到抛物线
的圆心为点M(Ⅰ)求点M到抛物线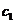 的准
的准 线的距离;
线的距离;
(Ⅱ)已知点P是抛物线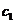 上一点(异于原点),过点P作圆
上一点(异于原点),过点P作圆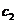 的两条切线,交抛物线
的两条切线,交抛物线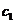 于A,B两点,若过M,P两点的直线
于A,B两点,若过M,P两点的直线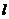 垂直于
垂直于 AB,求直线
AB,求直线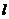 的方程
的方程
【解析】:(Ⅰ)由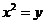 得准
得准 线方程为
线方程为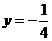 ,由
,由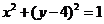 得M
得M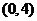 ,点M到抛物线
,点M到抛物线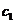 的准
的准 线的距离为
线的距离为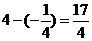
(Ⅱ)设点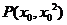 ,
,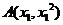 ,
,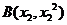 由题意得
由题意得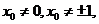
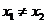 设过点
设过点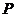 的圆
的圆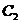 的切线方程为
的切线方程为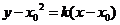 即
即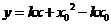 ① 则
① 则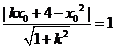
 求实数
求实数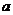 的取值范围,,使得对任意
的取值范围,,使得对任意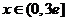 恒有
恒有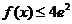 成立
成立
注: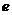 为自然对数的底数
为自然对数的底数
【解析】:(Ⅰ)由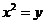 得准
得准 线方程为
线方程为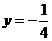 ,由
,由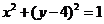 得M
得M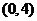 ,
,
点M到抛物线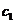 的准
的准 线的距离为
线的距离为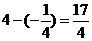
(Ⅱ)设点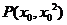 ,
,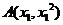 ,
,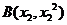 由题意得
由题意得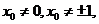
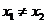 设过点
设过点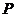 的圆
的圆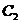 的切线方程为
的切线方程为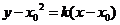 即
即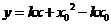 ① 则
① 则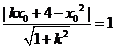
即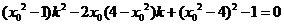 设
设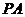 ,
,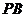 的斜率为
的斜率为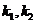 (
(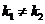 )则
)则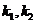 是上述方
是上述方
程的两个不相等的根,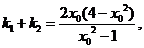
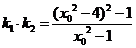 将代入①
将代入①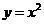 得
得
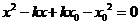 由于
由于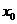 是方程的根故
是方程的根故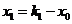 ,
,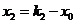 所以
所以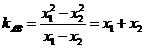 ,
,
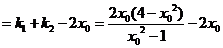 ,
,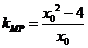
 所以
所以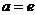 或
或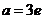
(Ⅱ)①当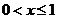 时, 对于任意实数
时, 对于任意实数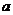 ,恒有
,恒有 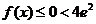 成立
成立
②当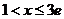 时,由题意,首先有
时,由题意,首先有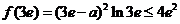
解得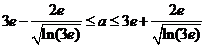 由(Ⅰ)知
由(Ⅰ)知 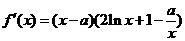
令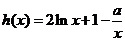 则
则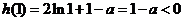 ,
,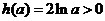
且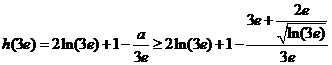
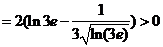
又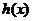 在
在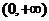 内单调递增,所以函数
内单调递增,所以函数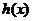 在
在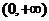 内有唯一零点,记此零点为
内有唯一零点,记此零点为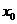 ,则
,则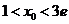 ,
,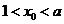 从而,当
从而,当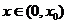 时,
时,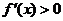 当
当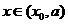 时
时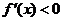
当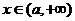 时
时 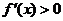 即
即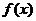 在
在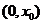 内单调递增,在
内单调递增,在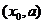 内单调递减,
内单调递减,
在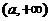 内单调递增。所以要使
内单调递增。所以要使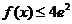 对
对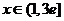 恒成立,
恒成立,
只要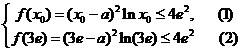 成立,由
成立,由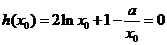 ,知
,知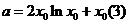 将(3)代入(1)得
将(3)代入(1)得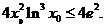 又
又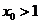 。注意到函数
。注意到函数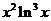 在
在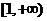 内单调递增,故
内单调递增,故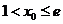
再由(3)以及函数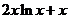 在
在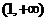 内单调递增,可得
内单调递增,可得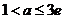 ,
,
由(2)解得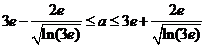 ,所以
,所以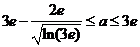
综上,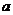 的取值范围为
的取值范围为