一、选择题(每小题4分,共40分)
1.(4分)(2014年贵州黔西 南州)﹣
南州)﹣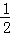 的倒数是( )
的倒数是( )
A.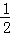 B. ﹣2 C. 2 D. ﹣
B. ﹣2 C. 2 D. ﹣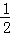
分析: 根据倒数的定义:若两个数的乘积是1,我们就称这两个数互为倒数可得答案.
解答: 解:﹣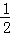 的倒数是﹣2.
的倒数是﹣2.
故选:B.
点评: 此题主要考查了倒数,关键是掌握两个倒数之积为1.
2.(4分)(2014年贵州黔西南州)不等式2x﹣4>0的解集为( )
A. x>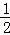 B. x>2 C. x>﹣2 D. x>8
B. x>2 C. x>﹣2 D. x>8
考点: 解一元一次不等式.
专题: 计算题.
分析: 根据不等式的性质先移项得到2x>4,然后把x的系数化为1即 可.
可.
解答: 解:移项得2x>4,
系数化为1得x>2.
故选B.
点评: 本题考查了解一元一次不等式:解一元一次不等式的基本步骤为:①去分母;②去括号;③移项;④合并同类项;⑤化系数为1.
3.(4分)(2014年贵州黔西南州)已知等腰三角形△ABC中,腰AB=8,底BC=5,则这个三角形的周长为( )
A. 21 B. 20 C. 19 D. 18
考点: 等腰三角形的性质.
分析: 由于等腰三角形的两腰相等,题目给出了腰和底,根据周长的定义即可求解.
解答: 解:8+8+5
=16+5
=21.
故这个三角形的周长为21.
故选:A.
点评: 考查了等腰三角形两腰相等的性质,以及三角形周长的定义.
4.(4分)(2014年贵州黔西南州)在一个不透明的 盒子中装有12个白球,若干个黄球,它们除颜色不同外,其余均相同.若从中随机摸出一个球是白球的概率是
盒子中装有12个白球,若干个黄球,它们除颜色不同外,其余均相同.若从中随机摸出一个球是白球的概率是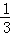 ,则黄球的个数为( )
,则黄球的个数为( )
A. 18 B. 20 C. 24 D. 28
考点: 概率公式.
分析: 首先设黄球的个数为x个,根据题意得: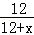 =
=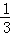 ,解此分式方程即可求得答案.
,解此分式方程即可求得答案.
解答: 解:设黄球的个数为x个,
根据题意得: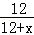 =
=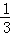 ,
,
解得:x=24,
经检验:x=24是原分式方程的解;
∴黄球的个数为24.
故选C.
点评: 此题考查了概率公式的应用 .用到的知识点为:概率=所求情况数与总情况数之比.
.用到的知识点为:概率=所求情况数与总情况数之比.
5.(4分)(2014年贵州黔西南州)如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )
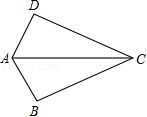
A. CB=CD B. ∠BAC=∠DAC C. ∠BCA=∠DCA D. ∠B=∠D=90°
考点: 全等三角形的判定.
分析: 本题要判定△ABC≌△ADC,已知AB=AD,AC是公共边,具备了两组边对应相等,故添加CB=CD、∠BAC=∠DAC、∠B=∠D=90°后可分别根据SSS、SAS、HL能判定△ABC≌△ADC,而添加∠BCA=∠DCA后则不能.
解答: 解:A、添加CB=CD,根据SSS,能判定△ABC≌△ADC,故A选项不符合题意;
B、添加∠BAC=∠DAC,根据SAS,能判定△ABC≌△ADC,故B选项不符合题意;
C、添加∠BCA=∠DCA时,不能判定△ABC≌△ADC,故C选项符合题意;
D、添加∠B=∠D=90°,根据HL,能判定△ABC≌△ADC,故D选项不符合题意;
故选:C.
点评: 本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
6.(4分)(2014年贵州黔西南州)已知两圆半径分别为3、5,圆心距为8,则这两圆的位置关系为( )
A. 外离 B. 内含 C. 相交 D. 外切
考点: 圆与圆的位置关系.
分析: 由⊙O1、⊙O2的半径分别是3、5,O1O2=8,根据两圆位置关系与圆心距d,两圆半径R,r的数量关系间的联系即可得出⊙O1和⊙O2的位置关系.
解答: 解:∵⊙O1、⊙O2的半径分别是3、5,O1O2=8,
又∵3+5=8,
∴⊙O1和⊙O2的位置关系是外切.
故选D.
点评: 此题考查了圆与圆的位置关系.解题的关键是掌握两圆位置关系与圆心距d,两圆半径R,r的数量关系间的联系.
7.(4分)(2014年贵州黔西南州)如图所示,是由5个相同的小正方体组合而成的几何体,它的左视图是( )
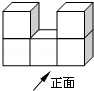
A. B.
B. C.
C. D.
D.
考点: 简单组合体的三视图.
分析: 找到从左面看所得到的图形即可,注意所有看到的棱都应表现在左视图中.
解答: 解:此几何体的左视图是“日”字形.
故选D.
点评: 本题考查了三视图的知识,左视图是从物体的左面看得到的视图.
8.(4分)(2014年贵州黔西南州)下列图形中,既是中心对称,又是轴对称图形的是( )
A.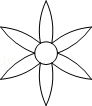 B.
B.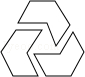 C.
C.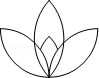 D.
D.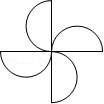
考点: 中心对称图形;轴对称图形.
分析: 根据中心对称图形的定义旋转180°后能够与原图形完全重合即是中心对称图形,以及轴对称图形的定义即可判断出.
解答: 解:A、∵此图形旋转180°后能与原图形重合,∴此图形是中心对称图形,也是轴对称图形,故此选项正确;
B、∵此图形旋转180°后能与原图形重合,∴此图形是中心对称图形,不是轴对称图形,故此选项错误;
C、此图形旋转180°后不能与原图形重合,此图形不是中心对称图形,是轴对称图形,故此选项错误;
D、∵此图形旋转180°后能与原图形重合,∴此图形是中心对称图形,不是轴对称图形,故此选项错误.
故选:A.
点评: 此题主要考查了中心对称图形与轴对称的定义,根据定义得出图形形状是解决问题的关键.
9.(4分)(2014年贵州黔西南州)已知如图,一次函数y=ax+b和反比例函数y=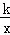 的图象相交于A、B两点,不等式ax+b>
的图象相交于A、B两点,不等式ax+b>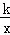 的解集为( )
的解集为( )
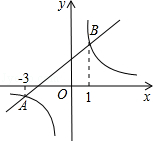
A. x<﹣3 B. ﹣3<x<0或x>1 C. x<﹣3或x>1 D. ﹣3<x<1
考点: 反比例函数与一次函数的交点问题.
专题: 数形结合.
分析: 观察函数图象得到当﹣3<x<0或x>1时,一次函数图象都在反比例函数图象上方,即有ax+b>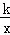 .
.
解答: 解:不等式ax+b>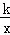 的解集为﹣3
的解集为﹣3 <x<0或x>1.
<x<0或x>1.
故选B.
点评: 本题考查了反比例函数与一次函数的交点问题:反比例函数与一次函数图象的交点坐标满足两函数解析 式.也考查了观察函数图象的能力.
式.也考查了观察函数图象的能力.
10.(4分)(2014年贵州黔西南州)甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑步500米,先到终点的人原地休息.已知甲先出发2秒.在跑步过程中,甲、乙两人的距离y(米)与乙出发的时间t(秒)之间的关系如图所示,给出以下结论:①a=8;②b=92;③c=123.其中正确的是( )
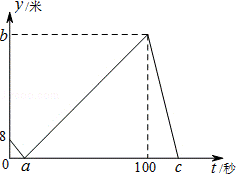
A. ①②③ B. 仅有①② C. 仅有①③ D. 仅有②③
考点: 一 次函数的应用.
次函数的应用.
专题: 行程问题;压轴题.
分析: 易得乙出发时,两人相距8m,除以时间2即为甲的速度;由于出现两人距离为0的情况,那么乙的速度较快.乙100s跑完总路程500可得乙的速度,进而求得100s时两人相距的距离可得b的值,同法求得两人距离为0时,相应的时间,让两人 相距的距离除以甲的速度,再加上100即为c的值.
相距的距离除以甲的速度,再加上100即为c的值.
解答: 解:甲的速度为:8÷2=4(米/秒);
乙的速度为:500÷100=5(米/秒);
b=5×100﹣4×(100+2) =92(米);
=92(米);
5a﹣4×(a+2)=0,
解得a=8,
c=100+92÷4=123(秒),
∴正确的有①②③.
故选A.
点评: 考查一次函数的应用;得到甲乙两人的速度是解决本题的突破点;得到相应行程的关系式是解决本题的关键.












