一、选择题(下列各题的备选答案中,只有一个是正确的,请将正确答案涂在答题卡上.每小题3分,共30分)
1.(3分)(2013•盘锦)﹣|﹣2|的值为( )
A. ﹣2 B. 2 C.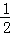 D. ﹣
D. ﹣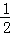
考点: 绝对值;相反数
分析: 根据绝对值的定义求解即可.
解答: 解:﹣|﹣2|=﹣2.
故选A.
点评: 本题考查了绝对值的定义:一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0.
2.(3分)(2013•盘锦)2013年8月31日,我国第12届全民运动会即将开幕,据某市财政预算统计,用于体育场馆建设的资金约为14000000,14000000用科学记数法表示为( )
A. 1.4×105 B. 1.4×106 C. 1.4×107 D. 1.4×108
考点: 科学记数法—表示较大的数.
分析: 科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.
解答: 解:将14000000用科学记数法表示为1.4×107.
故选C.
点评: 此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.
3.(3分)(2013•盘锦)下列调查中适合采用全面调查的是( )
A. 调查市场上某种白酒的塑化剂的含量
B. 调查鞋厂生产的鞋底能承受弯折次数
C. 了解某火车的一节车厢内感染禽流感病毒的人数
D. 了解某城市居民收看辽宁卫视的时间
考点: 全面调查与抽样调查.
分析: 由普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似.
解答: 解:A、数量较大,具有破坏性,适合抽查;
B、数量较大,具有破坏性,适合抽查;
C、事关重大,因而必须进行全面调查;
D、数量较大,不容易普查,适合抽查.
故选C.
点评: 本题考查了抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大时,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.
4.(3分)(2013•盘锦)如图下面几何体的左视图是( )
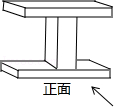
A. B.
B. C.
C. D.
D.
考点: 简单组合体的三视图
分析: 左视图即从物体左面看到的图形,找到从左面看所得到的图形即可,注意所有的看到的棱都应表现在左视图中.
解答: 解:从左面看易得三个竖直排列的长方形,且上下两个长方形的长大于宽,比较小,中间的长方形的宽大于长,比较大.
故选B.
点评: 本题考查了三视图的知识,难度一般,注意左视图是从物体的左面看得到的视图.
5.(3分)(2013•盘锦)下列计算正确的是( )
A. 3mn﹣3n=m B. (2m)3=6m3 C. m8÷m4=m2 D. 3m2•m=3m3
考点: 单项式乘单项式;合并同类项;幂的乘方与积的乘方;同底数幂的除法.
分析: 依据同底数的幂的除法、单项式的乘法以及积的乘方法则,合并同类项法则即可判断.
解答: 解:A、不是同类项,不能合并,选项错误;
B、(2m)3=8m3,选项错误;
C、m8÷m4=m4,选项错误;
D、正确.
故选D.
点评: 本题主要考查了合并同类项的法则,幂的乘方的性质,单项式的乘法法则,熟练掌握运算法则是解题的关键.
6.(3分)(2013•盘锦)某校举行健美操比赛,甲、乙两班个班选20名学生参加比赛,两个班参赛学生的平均身高都是1.65米,其方差分别是 =1.9,
=1.9,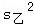 =2.4,则参赛学生身高比较整齐的班级是( )
=2.4,则参赛学生身高比较整齐的班级是( )
A. 甲班 B. 乙班 C. 同样整齐 D. 无法确定
考点: 方差.
分析: 根据方差的意义可作出判断.方差是用来衡量一组数据波动大小的量,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.
解答: 解:∵ =1.9,
=1.9, =2.4,
=2.4,
∴ <
< ,
,
∴参赛学生身高比较整齐的班级是甲班,
故选:A.
点评: 此题主要考查了方差,方差是反映一组数据的波动大小的一个量.方差越大,则平均值的离散程度越大,稳定性也越小;反之,则它与其平均值的离散程度越小,稳定性越好.
7.(3分)(2013•盘锦)某班为了解学生“多读书、读好书”活动的开展情况,对该班50名学生一周阅读课外书的时间进行了统计,统计结果如下:
阅读时间(小时) | 1 | 2 | 3 | 4 | 5 |
人数(人) | 7 | 19 | 13 | 7 | 4 |
由上表知,这50名学生周一阅读课外书时间的众数和中位数分别为( )
A. 19,13 B. 19,19 C. 2,3 D. 2,2
考点: 众数;中位数.
分析: 根据众数、中位数的定义,结合表格数据进行判断即可.
解答: 解:阅读课外书时间学生数最多的是2小时,
故众数为3;
共50名学生,中位数在第25、26名学生处,第25、26名学生阅读2小时,
故中位数为2;
故选D.
点评: 本题考查了众数及中位数的知识,解答本题的关键是熟练掌握众数及中位数的定义,注意仔细审题题目要求的是:“阅读课外书时间”的众数和中位数.
8.(3分)(2013•盘锦)如图,将一副三角板和一张对边平行的纸条按下列方式摆放,两个三角板的一直角边重合,含30°角的直角三角板的斜边与纸条一边重合,含45°角的三角板的一个顶点在纸条的另一边上,则∠1的度数是( )
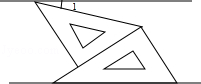
A. 30° B. 20° C. 15° D. 14°
考点: 平行线的性质.
分析: 延长两三角板重合的边与直尺相交,根据两直线平行,内错角相等求出∠2,再利用三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解.
解答: 解:如图,∠2=30°,
∠1=∠3﹣∠2=45°﹣30°=15°.
故选C.
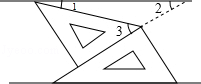
点评: 本题考查了平行线的性质,三角板的知识,熟记平行线的性质,三角板的度数是解题的关键.
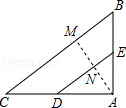
9.(3分)(2013•盘锦)如图,△ABC中,AB=6,AC=8,BC=10,D、E分别是AC、AB的中点,则以DE为直径的圆与BC的位置关系是( )
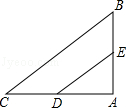
A. 相交 B. 相切 C. 相离 D. 无法确定
考点: 直线与圆的位置关系.
分析: 首先根据三角形面积求出AM的长,进而得出直线BC与DE的距离,进而得出直线与圆的位置关系.
解答: 解:过点A作AM⊥BC于点M,交DE于点N,
∴AM×BC=AC×AB,
∴AM=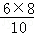 =4.8,
=4.8,
∵D、E分别是AC、AB的中点,
∴DE∥BC,DE=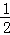 BC=5,
BC=5,
∴AN=MN=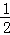 AM,
AM,
∴MN=2.4,
∴以DE为直径的圆半径为2.5,
∵r>2.5>2.4,
∴以DE为直径的圆与BC的位置关系是:相交.
故选:A.
点评: 本题考查了直线和圆的位置关系,利用中位线定理比较出BC到圆心的距离与半径的关系是解题的关键.
10.(3分)(2013•盘锦)如图,将边长为4的正方形ABCD的一边BC与直角边分别是2和4的Rt△GEF的一边GF重合.正方形ABCD以每秒1个单位长度的速度沿GE向右匀速运动,当点A和点E重合时正方形停止运动.设正方形的运动时间为t秒,正方形ABCD与Rt△GEF重叠部分面积为s,则s关于t的函数图象为( )
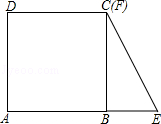
A.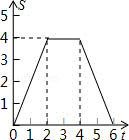 B.
B.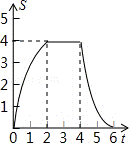 C.
C.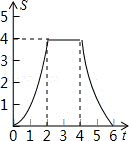 D.
D.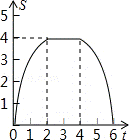
考点: 动点问题的函数图象.
分析: 分类讨论:当0≤t≤2时,BG=t,BE=2﹣t,运用△EBP∽△EGF的相似比可表示PB=1﹣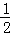 t,S为梯形PBGF的面积,则S=
t,S为梯形PBGF的面积,则S=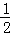 (1﹣
(1﹣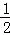 t+4)•t=﹣
t+4)•t=﹣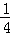 (t﹣5)2+
(t﹣5)2+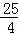 ,其图象为开口向下的抛物线的一部分;当2<t≤4时,S=
,其图象为开口向下的抛物线的一部分;当2<t≤4时,S=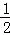 FG•GE=4,其图象为平行于x轴的一条线段;当4<t≤6时,GA=t﹣4,AE=6﹣t,运用△EAP∽△EGF的相似比可得到PA=2(6﹣t),∴S为三角形PAE的面积,则S=
FG•GE=4,其图象为平行于x轴的一条线段;当4<t≤6时,GA=t﹣4,AE=6﹣t,运用△EAP∽△EGF的相似比可得到PA=2(6﹣t),∴S为三角形PAE的面积,则S=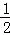 (t﹣6)2,其图象为开口向上的抛物线的一部分.
(t﹣6)2,其图象为开口向上的抛物线的一部分.
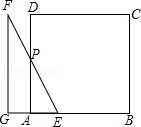
解答: 解:当0≤t≤2时,如图,
BG=t,BE=2﹣t,
∵PB∥GF,
∴△EBP∽△EGF,
∴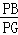 =
=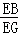 ,即
,即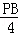 =
=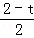 ,
,
∴PB=1﹣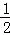 t,
t,
∴S=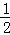 (PB+FG)•GB=
(PB+FG)•GB=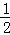 (1﹣
(1﹣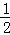 t+4)•t=﹣
t+4)•t=﹣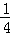 (t﹣5)2+
(t﹣5)2+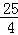 ;
;
当2<t≤4时,S=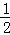 FG•GE=4;
FG•GE=4;
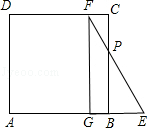
当4<t≤6时,如图,
GA=t﹣4,AE=6﹣t,
∵PA∥GF,
∴△EAP∽△EGF,
∴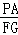 =
=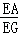 ,即
,即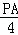 =
=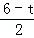 ,
,
∴PA=2(6﹣t),
∴S=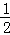 PA•AE=
PA•AE=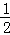 •2(6﹣t)(6﹣t)
•2(6﹣t)(6﹣t)
=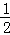 (t﹣6)2,
(t﹣6)2,
综上所述,当0≤t≤2时,s关于t的函数图象为开口向下的抛物线的一部分;当2<t≤4时,s关于t的函数图象为平行于x轴的一条线段;当4<t≤6时,s关于t的函数图象为开口向上的抛物线的一部分.
故选B.
点评: 本题考查了动点问题的函数图象:先根据几何性质得到与动点有关的两变量之间的函数关系,然后利用函数解析式和函数性质画出其函数图象,注意自变量的取值范围.












