一、选择题(12小题,每小题3分)
1.(3分)(2013•眉山)﹣2的倒数是( )
A. 2 B. 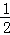 C. ﹣
C. ﹣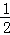 D. ﹣0.2
D. ﹣0.2
考点: 倒数.
专题: 计算题.
分析: 根据乘积为1的两数互为倒数,即可得出答案.
解答: 解:﹣2的倒数为﹣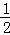 .
.
故选C.
点评: 此题考查了倒数的定义,属于基础题,关键是掌握乘积为1的两数互为倒数.
2.(3分)(2013•眉山)下列计算正确的是( )
A. a4+a2=a6 B. 2a•4a=8a C. a5÷a2=a3 D. (a2)3=a5
考点: 单项式乘单项式;合并同类项;幂的乘方与积的乘方;同底数幂的除法.
专题: 计算题
分析: A、原式不能合并,错误;
B、利用单项式乘单项式法则计算得到结果,即可作出判断;
C、利用同底数幂的除法法则计算得到结果,即可作出判断;
D、利用幂的乘方运算法则计算得到结果,即可作出判断.
解答: 解:A、原式不能合并,错误;
B、2a•4a=8a2,本选项错误;
C、a5÷a2=a3,本选项正确;
D、(a2)3=a6,本选项错误,
故选C
点评: 此题考查了单项式乘单项式,合并同类项,幂的乘方与积的乘方,以及同底数幂的除法,熟练掌握运算法则是解本题的关键.
3.(3分)(2013•眉山)某市地铁一号与地铁二号线接通后,该市交通通行和转换能力成倍增长,该工程投资预算约为930000万元,这一数据用科学记数法表示为( )
A. 9.3×105万元 B. 9.3×106万元 C. 0.93×106万元 D. 9.3×104万元
考点: 科学记数法—表示较大的数.
分析: 科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.
解答: 解:将930000用科学记数法表示为9.3×105.
故选B.
点评: 此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.
4.(3分)(2013•眉山)下列图形是中心对称图形的是( )
A.  B.
B. 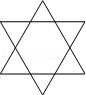 C.
C. 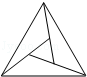 D.
D. 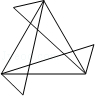
考点: 中心对称图形.
分析: 根据中心对称的定义,结合所给图形进行判断即可.
解答: 解:A、不是中心对称图形,故本选项错误;
B、是中心对称图形,故本选项正确;
C、不是中心对称图形,故本选项错误;
D、不是中心对称图形,故本选项错误;
故选B.
点评: 本题考查了中心对称图形的知识,中心对称图形是要寻找对称中心,旋转180度后与原图重合.
5.(3分)(2013•眉山)一个正多边形的每个外角都是36°,这个正多边形的边数是( )
A. 9 B. 10 C. 11 D. 12
考点: 多边形内角与外角.
分析: 利用多边形的外角和是360度,正多边形的每个外角都是36°,即可求出答案.
解答: 解:360°÷36°=10,
则这个正多边形的边数是10.
故选B.
点评: 本题主要考查了多边形的外角和定理.是需要识记的内容,要求同学们掌握多边形的外角和为360°.
6.(3分)(2013•眉山)下列命题,其中真命题是( )
A. 方程x2=x的解是x=1
B. 6的平方根是±3
C. 有两边和一个角分别对应相等的两个三角形全等
D. 连接任意四边形各边中点的四边形是平行四边形
考点: 命题与定理
分析: 根据一元二次方程的解、平方根的定义、全等三角形的判定和平行四边形的判定分别对每一项进行分析,即可得出答案.
解答: 解:A、方程x2=x的解是x=1或0,故原命题是假命题;
B、6的平方根是±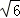 ,故原命题是假命题;
,故原命题是假命题;
C、有两边及其夹角分别对应相等的两个三角形全等,故原命题是假命题;
D、连接任意四边形各边中点的四边形是平行四边形,故原命题是真命题;
故选:D.
点评: 此题考查了命题与定理,正确的命题叫真命题,错误的命题叫做假命题.判断命题的真假关键是要熟悉课本中的性质定理.
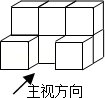
7.(3分)(2013•眉山)如图是小强用八块相同的小正方体搭建的一个积木,它的左视图是( )
A.  B.
B.  C.
C.  D.
D. 
考点: 简单组合体的三视图.
分析: 左视图从左往右,2列正方形的个数依次为2,1,依此画出图形即可求出答案.
解答: 解:左视图从左往右,2列正方形的个数依次为2,1;
依此画出图形 .
.
故选D.
点评: 此题主要考查了画三视图的知识,用到的知识点为:主视图,左视图,俯视图分别是从物体的正面,左面,上面看得到的图形.
8.(3分)(2013•眉山)王明同学随机抽查某市10个小区所得到的绿化率情况,结果如下表:
小区绿化率(%) | 20 | 25 | 30 | 32 |
小区个数 | 2 | 4 | 3 | 1 |
则关于这10个小区的绿化率情况,下列说法错误的是( )
A. 极差是13% B. 众数是25% C. 中位数是25% D. 平均数是26.2%
考点: 极差;加权平均数;中位数;众数
分析: 根据极差、众数、中位数、平均数的定义求解即可.
解答: 解:由表格可知,极差为:32%﹣20%=12%,
众数为:25%,
中位数为:25%,
平均数为: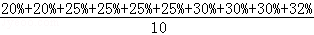 =26.2%,
=26.2%,
故选A.
点评: 本题考查了极差、众数、中位数、平均数的知识,属于基础题,解题的关键是掌握各知识点的定义.
9.(3分)(2013•眉山)用一圆心角为120°,半径为6cm的扇形做成一个圆锥的侧面,这个圆锥的底面的半径是( )
A. 1cm B. 2cm C. 3cm D. 4cm
考点: 圆锥的计算.
分析: 利用圆锥的侧面展开图中扇形的弧长等于圆锥底面的周长可得.
解答: 解:设此圆锥的底面半径为r,由题意,得
2πr=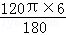 ,
,
解得r=2cm.
故选B.
点评: 本题考查了圆锥的计算,圆锥的侧面展开图是一个扇形,此扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.本题就是把扇形的弧长等于圆锥底面周长作为相等关系,列方程求解.
10.(3分)(2013•眉山)不等式组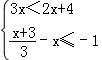 的解集在数轴上表示为( )
的解集在数轴上表示为( )
A. 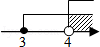 B.
B.  C.
C. 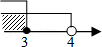 D.
D. 
考点: 在数轴上表示不等式的解集;解一元一次不等式组.
专题: 计算题.
分析: 分别求出各不等式的解集,再求出其公共解集即可.
解答: 解: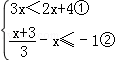 ,由①得,x<4;由②得,x≥3,
,由①得,x<4;由②得,x≥3,
故此不等式组的解集为:3≤x<4,
在数轴上表示为:
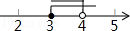
故选D.
点评: 本题考查的是在数轴上表示一元一次不等式组的解集,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.
11.(3分)(2013•眉山)若实数a,b,c满足a+b+c=0,且a<b<c,则函数y=cx+a的图象可能是( )
A. 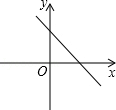 B.
B. 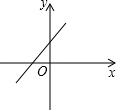 C.
C. 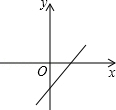 D.
D. 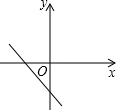
考点: 一次函数图象与系数的关系.
专题: 存在型.
分析: 先判断出a是负数,c是正数,然后根据一次函数图象与系数的关系确定图象经过的象限以及与y轴的交点的位置即可得解.
解答: 解:∵a+b+c=0,且a<b<c,
∴a<0,c>0,(b的正负情况不能确定),
∵a<0,
∴函数y=cx+a的图象与y轴负半轴相交,
∵c>0,
∴函数y=cx+a的图象经过第一象限,
∴函数y=cx+a的图象经过第一、三、四象限.
故选C.
点评: 本题主要考查了一次函数图象与系数的关系,先确定出a、c的正负情况是解题的关键,也是本题的难点.
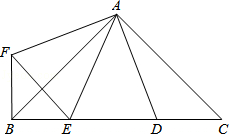
12.(3分)(2013•眉山)如图,∠BAC=∠DAF=90°,AB=AC,AD=AF,点D、E为BC边上的两点,且∠DAE=45°,连接EF、BF,则下列结论:
①△AED≌△AEF;②△ABE∽△ACD;③BE+DC>DE;④BE2+DC2=DE2,
其中正确的有( )个.
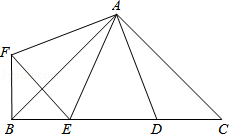
A. 1 B. 2 C. 3 D. 4
考点: 相似三角形的判定与性质;全等三角形的判定与性质;勾股定理.
分析: 根据∠DAF=90°,∠DAE=45°,得出∠FAE=45°,利用SAS证明△AED≌△AEF,判定①正确;
如果△ABE∽△ACD,那么∠BAE=∠CAD,由∠ABE=∠C=45°,则∠AED=∠ADE,AD=AE,而由已知不能得出此条件,判定②错误;
先由∠BAC=∠DAF=90°,得出∠CAD=∠BAF,再利用SAS证明△ACD≌△ABF,得出CD=BF,又①知DE=EF,那么在△BEF中根据三角形两边之和大于第三边可得BE+BF>EF,等量代换后判定③正确;
先由△ACD≌△ABF,得出∠C=∠ABF=45°,进而得出∠EBF=90°,然后在Rt△BEF中,运用勾股定理得出BE2+BF2=EF2,等量代换后判定④正确.
解答: 解:①∵∠DAF=90°,∠DAE=45°,
∴∠FAE=∠DAF﹣∠DAE=45°.
在△AED与△AEF中,
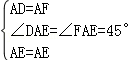 ,
,
∴△AED≌△AEF(SAS),①正确;
②∵∠BAC=90°,AB=AC,
∴∠ABE=∠C=45°.
∵点D、E为BC边上的两点,∠DAE=45°,
∴AD与AE不一定相等,∠AED与∠ADE不一定相等,
∵∠AED=45°+∠BAE,∠ADE=45°+∠CAD,
∴∠BAE与∠CAD不一定相等,
∴△ABE与△ACD不一定相似,②错误;
③∵∠BAC=∠DAF=90°,
∴∠BAC﹣∠BAD=∠DAF﹣∠BAD,即∠CAD=∠BAF.
在△ACD与△ABF中,
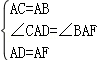 ,
,
∴△ACD≌△ABF(SAS),
∴CD=BF,
由①知△AED≌△AEF,
∴DE=EF.
在△BEF中,∵BE+BF>EF,
∴BE+DC>DE,③正确;
④由③知△ACD≌△ABF,
∴∠C=∠ABF=45°,
∵∠ABE=45°,
∴∠EBF=∠ABE+∠ABF=90°.
在Rt△BEF中,由勾股定理,得BE2+BF2=EF2,
∵BF=DC,EF=DE,
∴BE2+DC2=DE2,④正确.
所以正确的结论有①③④.
故选C.
点评: 本题考查了勾股定理,全等三角形的判定与性质,等腰直角直角三角形的性质,三角形三边关系定理,相似三角形的判定,此题涉及的知识面比较广,解题时要注意仔细分析,有一定难度.












