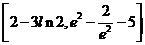19. 【思路】由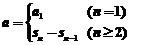 可求出
可求出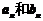 ,这是数列中求通项的常用方法之一,在求出
,这是数列中求通项的常用方法之一,在求出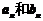 后,进而得到
后,进而得到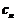 ,接下来用作差法来比较大小,这也是一常用方法。
,接下来用作差法来比较大小,这也是一常用方法。
【解析】(1)由于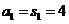
当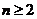 时,
时, 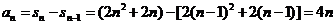
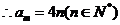
又当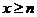 时
时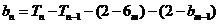
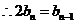
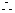 数列
数列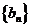 项与等比数列,其首项为1,公比为
项与等比数列,其首项为1,公比为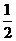
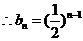
(2)由(1)知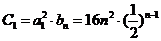
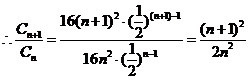
由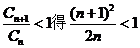 即
即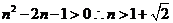 即
即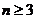
又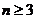 时
时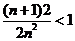 成立,即
成立,即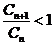 由于
由于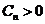 恒成立.
恒成立.
因此,当且仅当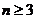 时,
时, 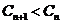
20. 【思路】根据空间线面关系可证线线垂直,由分割法可求得多面体体积,体现的是一种部分与整体的基本思想。
【解析】(1)由于EA=ED且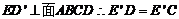
 点E
点E 在线段AD的垂直平分线上,同理点F
在线段AD的垂直平分线上,同理点F 在线段BC的垂直平分线上.
在线段BC的垂直平分线上.
又ABCD是四方形
 线段BC的垂直平分线也就是线段AD的垂直平分线
线段BC的垂直平分线也就是线段AD的垂直平分线
即点E F
F 都居线段AD的垂直平分线上.
都居线段AD的垂直平分线上.
所以,直线E F
F 垂直平分线段AD.
垂直平分线段AD.
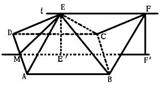 (2)连接EB、EC由题意知多面体ABCD可分割成正四棱锥E—ABCD和正四面体E—BCF两部分.设AD中点为M,在Rt△MEE
(2)连接EB、EC由题意知多面体ABCD可分割成正四棱锥E—ABCD和正四面体E—BCF两部分.设AD中点为M,在Rt△MEE 中,由于ME
中,由于ME =1,
=1, 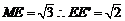 .
.
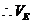 —ABCD
—ABCD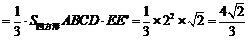
又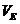 —BCF=VC-BEF=VC-BEA=VE-ABC
—BCF=VC-BEF=VC-BEA=VE-ABC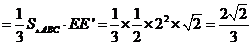
 多面体ABCDEF的体积为VE—ABCD+VE—BCF=
多面体ABCDEF的体积为VE—ABCD+VE—BCF=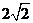
21. 【思路】由求导可判断得单调性,同时要注意对参数的讨论,即不能漏掉,也不能重复。第二问就根据第一问中所涉及到的单调性来求函数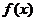 在
在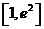 上的值域。
上的值域。
【解析】(1)由于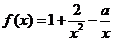
令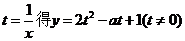
①当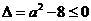 ,即
,即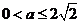 时,
时, 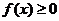 恒成立.
恒成立.
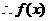 在(-∞,0)及(0,+∞)上都是增函数.
在(-∞,0)及(0,+∞)上都是增函数.
②当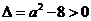 ,即
,即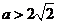 时
时
由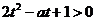 得
得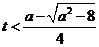 或
或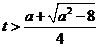
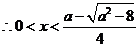 或
或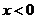 或
或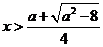
又由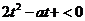 得
得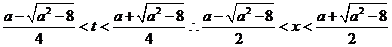
综上①当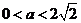 时,
时, 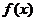 在
在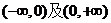 上都是增函数.
上都是增函数.
②当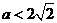 时,
时, 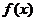 在
在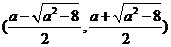 上是减函数,
上是减函数,
在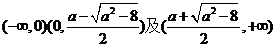 上都是增函数.
上都是增函数.
(2)当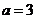 时,由(1)知
时,由(1)知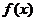 在
在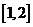 上是减函数.
上是减函数.
在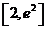 上是增函数.
上是增函数.
又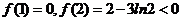
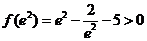
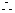 函数
函数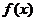 在
在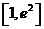 上的值域为
上的值域为