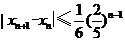第Ⅰ卷
一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的(本大题共12小题,每小题5分,共60分)
1.设不等式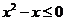 的解集为M,函数
的解集为M,函数 的定义域为N,则
的定义域为N,则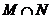 为
为
(A)[0,1) (B)(0,1) (C)[0,1] (D)(-1,0]
2.已知z是纯虚数,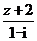 是实数,那么z等于
是实数,那么z等于
(A)2i (B)i (C)-i (D)-2i
3.函数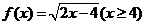 的反函数为
的反函数为
(A)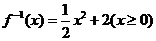 (B)
(B) 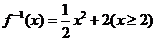
(C)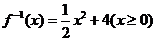 (D)
(D) 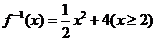
4.过原点且倾斜角为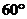 的直线被圆
的直线被圆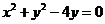 所截得的弦长为
所截得的弦长为
(A)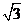 (B)2 (C)
(B)2 (C)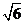 (D)2
(D)2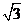


5.若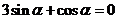 ,则
,则 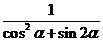 的值为
的值为
(A)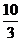 (B)
(B)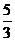 (C)
(C)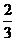 (D)
(D) 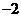


6.若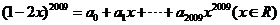 ,则
,则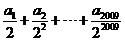 的值为
的值为
(A)2 (B)0 (C)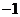 (D)
(D) 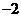


7.“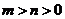 ”是“方程
”是“方程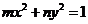 表示焦点在y轴上的椭圆”的
表示焦点在y轴上的椭圆”的
(A)充分而不必要条件 (B)必要而不充分条件
(C)充要条件  (D) 既不充分也不必要条件
(D) 既不充分也不必要条件
8.在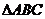 中,M是BC的中点,AM=1,点P在AM上且满足
中,M是BC的中点,AM=1,点P在AM上且满足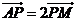 ,则
,则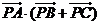 等于
等于
(A)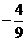 (B)
(B)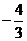 (C)
(C)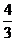 (D)
(D) 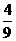
9.从0,1,2,3,4,5这六个数字中任取两个奇数和两个偶数,组成没有重复数字的四位数的个数为
(A)300 (B)216 (C) 180 (D)162
10.若正方体的棱长为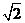 ,则以该正方体各个面的中心为顶点的凸多面体的体积为
,则以该正方体各个面的中心为顶点的凸多面体的体积为
(A)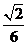 (B)
(B) 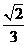 (C)
(C) 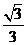 (D)
(D) 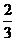
11.若x,y满足约束条件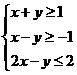 ,目标函数
,目标函数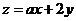 仅在点(1,0)处取得最小值,则a的取值范围是
仅在点(1,0)处取得最小值,则a的取值范围是
(A) (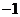 ,2 ) (B) (
,2 ) (B) (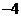 ,2 ) (C)
,2 ) (C) 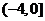 (D)
(D) 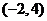
12.定义在R上的偶函数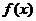 满足:对任意的
满足:对任意的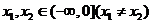 ,有
,有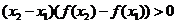 .则当
.则当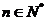 时,有
时,有
(A)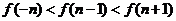 (B)
(B) 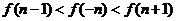
(C) (C)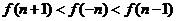 (D)
(D) 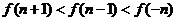
第Ⅱ卷
二、填空题:把答案填在答题卡相应题号后的横线上(本大题共4小题,每小题4分,共16分).
13.设等差数列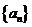 的前n项和为
的前n项和为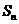 ,若
,若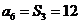 ,则
,则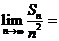 ______________.
______________.
14.某班有36名同学参加数学、物理、化学课外探究小组,每名同学至多参加两个小组,已知参加数学、物理、化学小组的人数分别为26,15,13,同时参加数学和物理小组的有6人,同时参加物理和化学小组的有4人,则同时参加数学和化学小组的有_________人。
15.如图球O的半径为2,圆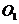 是一小圆,
是一小圆,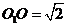 ,A、B 是圆
,A、B 是圆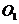 上两点,若A,B两点间的球面距离为
上两点,若A,B两点间的球面距离为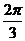 ,则
,则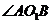 = _________ .
= _________ .
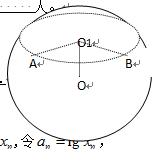
16.设曲线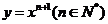 在点(1,1)处的切线与x轴的交点的横坐标为
在点(1,1)处的切线与x轴的交点的横坐标为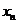 ,令
,令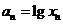 ,则
,则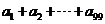 的值为 _________.
的值为 _________.
三、解答题:解答应写出文字说明,证明过程或演算步骤(本大题共6小题,共74分)
17.(本小题满分12分)
已知函数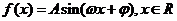 (其中
(其中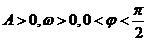 )的图象与x轴的交点中,相邻两个交点之间的距离为
)的图象与x轴的交点中,相邻两个交点之间的距离为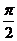 ,且图象上一个最低点为
,且图象上一个最低点为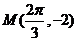 .
.
(Ⅰ)求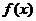 的解析式;(Ⅱ)当
的解析式;(Ⅱ)当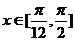 ,求
,求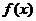 的值域.
的值域.
18.(本小题满分12分)
如图,在直三棱柱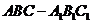 中, AB=1,
中, AB=1,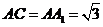 ,∠ABC=60
,∠ABC=60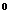 .
.
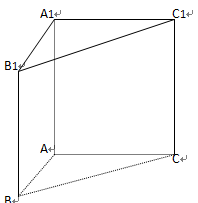
(Ⅰ)证明: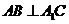 ;
;
(Ⅱ)求二面角A—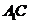 —B的大小。
—B的大小。
19.(本小题满分12分)
某食品企业一个月内被消费者投诉的次数用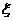 表示,椐统计,随机变量
表示,椐统计,随机变量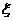 的概率分布如下:
的概率分布如下:
| 0 | 1 | 2 | 3 |
p | 0.1 | 0.3 | 2a | a |
(Ⅰ)求a的值和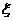 的数学期望;
的数学期望;
(Ⅱ)假设一月份与二月份被消费者投诉的次数互不影响,求该企业在这两个月内共被消费者投诉2次的概率。
20.(本小题满分12分)
已知函数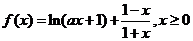 ,其中
,其中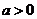
 若
若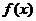 在x=1处取得极值,求a的值;
在x=1处取得极值,求a的值;
 求
求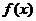 的单调区间;
的单调区间;
(Ⅲ)若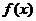 的最小值为1,求a的取值范围。
的最小值为1,求a的取值范围。
21.(本小题满分12分)
已知双曲线C的方程为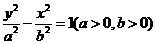 ,离心率
,离心率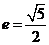 ,顶点到渐近线的距离为
,顶点到渐近线的距离为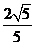 。
。
(I)求双曲线C的方程;
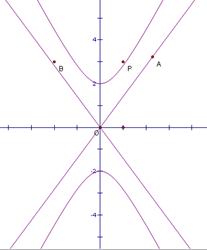
(II)如图,P是双曲线C上一点,A,B两点在双曲线C的两条渐近线上,且分别位于第一、二象限,若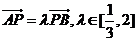 ,求
,求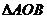 面积的取值范围。
面积的取值范围。
22.(本小题满分12分)
已知数列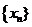 满足,
满足, 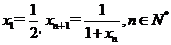 .
.
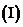 猜想数列
猜想数列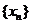 的单调性,并证明你的结论;
的单调性,并证明你的结论;
(Ⅱ)证明: