一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的(本大题共10小题,每小题5分,共50分).
1.集合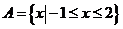 ,
,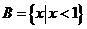 ,则A∩B=
,则A∩B=
(A) 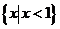 (B)
(B)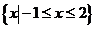
(C) 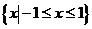 (D)
(D)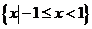
【答案】D
【命题意图】本题主要考查集合基本运算中的交集的运算问题.
【解析】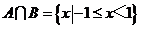 .故选D.
.故选D.
2.复数z=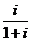 在复平面上对应的点位于
在复平面上对应的点位于
(A)第一象限 (B)第二象限 (C)第三象限 (D)第四象限
【答案】A
【命题意图】本题主要考查复数的除法运算问题.
【解析】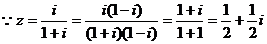 ,
,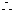 对应点
对应点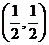 在第一象限.
在第一象限.
3.函数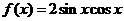 是
是
(A)最小正周期为2π的奇函数 (B)最小正周期为2π的偶函数
(C)最 小正周期为π的奇函数 (D)最小正周期为π的偶函数
小正周期为π的奇函数 (D)最小正周期为π的偶函数
【答案】C
【命题意图】本题主要考三角函数周期及奇偶性定义.
【解析】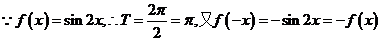 ,
,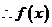 为奇函数.故选C.
为奇函数.故选C.
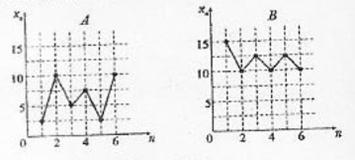
4.如图,样本A和B分别取自两个不同的总体,它们的 样本平均数分别为
样本平均数分别为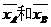 ,样本标准差分别为
,样本标准差分别为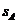 和
和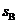 ,则
,则
(A) 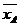 >
>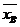 ,
,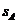 >
>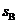
(B) 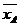 <
<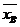 ,
,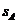 >
>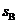
(C) 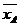 >
>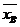 ,
,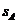 <
<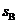
( D)
D) 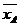 <
<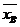 ,
,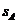 <
<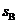
【答案】B
【命题意图】本题主要考查对统计里面的均值及样本标准差的公式掌握.
【解析】由图知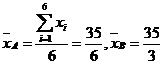 ,由图可知样本A的曲线波动大,则
,由图可知样本A的曲线波动大,则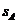 >
>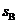 .故选B.
.故选B.
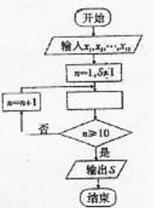
5.右图是求x1,x2,…,x10的乘积S的程序框图,图中 空白框中应填入的内容为
空白框中应填入的内容为
(A)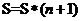
(B)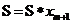
(C)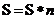
(D)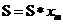
【答案】D
【命题意图】本题主要考查程序框图的运用,重点是分析循环结构.
【解析】由图知空白框处在一个循环体中,开始时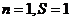 每循环一次
每循环一次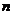 增加1,由输出结果可知第K次循环后
增加1,由输出结果可知第K次循环后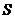 应为循环前的
应为循环前的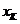 倍,故选D.
倍,故选D.
6.“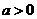 ”是“
”是“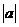 >0”的
>0”的
(A)充分不必要条件 (B)必要不充分条件
(C)充要条件 (D)既不充分也不必要条件
【答案】A
【命题意图】本题主要考查对充要条件的理解.
【解析】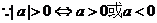 .故选A.
.故选A.
7.下列四类函数中,具有性质“对任意的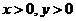 ,函数
,函数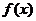 满足
满足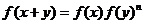 ”的是
”的是
(A)幂函数 (B)对数函数
(C)指数函数 (D)余弦 函数【答案】C
函数【答案】C
【命题意图】本题主要考查高中四个基本函数形式及运算法则.
【解析】因选项中四个函数解析式分别为: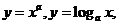
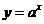
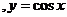 ,故由运算法则知选C.
,故由运算法则知选C.
8.若某空间几何体的三视图如图所示,则该几何体的体积是
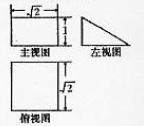
(A)2 (B)1
(C)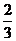 (D)
(D)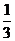
【答案】B
【命题意图】本题主要考查三视图与原图形之间的关系.
【解析】由三视图知几何体为直三棱柱,底面为直角三角形,两直角边分别为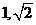 ,高为
,高为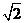 ,体积为1,故选B.
,体积为1,故选B.
9.已知抛物线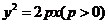 的准线与圆
的准线与圆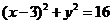 相切,则p的值为
相切,则p的值为
(A)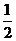 (B)1 (C)2 (D)4
(B)1 (C)2 (D)4
【答案】C
【命题意图】本题主要考查抛物线准线及直线与圆的位置关系的运用.
【解析】因抛物线的准线方程为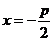 ,圆心
,圆心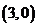 ,
,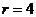 ,
,
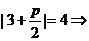
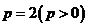 ,故选C.
,故选C.
10.某学校要召开学生 代表大会,规定各班每10人推选一名代表,当各班人数除以10的余数大于6时再增选一名代表.那么,各班可推选代表人数y与该班人数
代表大会,规定各班每10人推选一名代表,当各班人数除以10的余数大于6时再增选一名代表.那么,各班可推选代表人数y与该班人数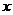 之间的函数关系用取整函数
之间的函数关系用取整函数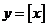 ([x]表示不大于
([x]表示不大于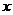 的最大整数)可以表示为
的最大整数)可以表示为
(A)y=[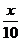 ] (B)y=[
] (B)y=[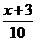 ] (C)y=[
] (C)y=[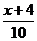 ] (D)y=[
] (D)y=[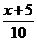 ]
]

二、填空题:把答案填在答题卡相应题号后的横线上(本 大题共5小题,每小题5分,共25分).
大题共5小题,每小题5分,共25分).
11.观察下列等式: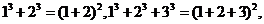
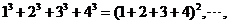 根据上述规律,第四个等式为 .
根据上述规律,第四个等式为 .
【答案】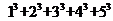 =
=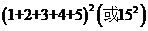
【命题意图】本题主要考查归纳推理的能力.
【解析】由前三个式子看出,第K个等式左边为从1到K+1的立方和,右边为这K+1个数和的平方,故第四个等式为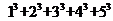
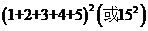 .
.
12.已知向量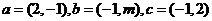 若
若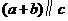 ,则m= .
,则m= .
【答案】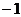
【命题意图】本题主要考查向量的线性运算及向量平行的充要条件.
【解析】由已知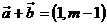 ,
,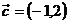 ,由
,由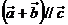 的充要条件可得
的充要条件可得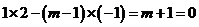 ,∴
,∴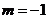 .
.
13.已知函数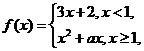 若
若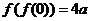 ,则实数
,则实数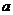 = .
= .
【答案】2
【命题意图】本题主要考查复合函数求值的方法.
【解析】由题知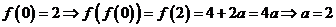 .
.
14.设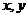 满足约束条件
满足约束条件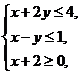 ,则目标函数
,则目标函数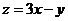 的最大值为 .
的最大值为 .

15.(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评 分)
分)
A.(不等式选做题)不等式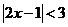 的解集为 .
的解集为 .
【答案】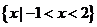
【命题意图】本题主要考查绝对值不等式的解法.
【解析】原不等式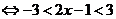 ,故解集为
,故解集为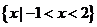 .
.
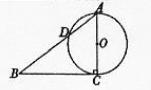
B.(几何证明选做题)如图,已知Rt△ABC的两条直角边AC,BC的长分别为3cm,4cm,以AC为直径的圆与AB交于点D,则BD= cm.
【答案】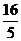
【命题意图】本题主要考查平面几何的切割线定理的运用.
【解析】由题知边AB=5cm,由切割线定理得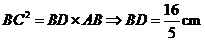 .
.
C.(坐标系与参数方程选做题)参数方程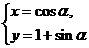 (
(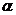 为参数)化成普通方程为 .
为参数)化成普通方程为 .
【答案】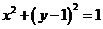
【命题意图】本题主要考查参数方程与三角公式灵活运用.
【解析】由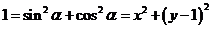 ,即
,即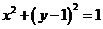 .
.
三、解答题:解答应写出文字说明、证明过程或演算步骤(本大题共6小题,共75分).
16.(本小题满分12分)
已知{an}是公差不为零的等差数列,a1=1,且a1,a3,a9成等比数列.
(Ⅰ)求数列{an}的通项; (Ⅱ)求数列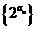 的前n项和Sn.
的前n项和Sn.

17.(本小题满分12分)
在△ABC中,已知B=45°,D是BC边上的一点,AD=10,AC=14,DC=6,求AB的长.
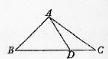
【命题意图】本题主要考查利用正余弦定理求解三角形问题,试题比较基础,入手比较容易.是一道立足基础,灵活运用正余弦定理来求三角形中的边角问题的综合性试题.
【参考答案】解:在△ADC中,AD=10,AC=14,DC=6,
由余弦定理得cos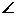
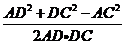 =
=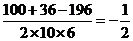 ,
,
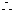
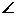 ADC=120°,
ADC=120°, 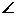 ADB=60°
ADB=60°
在△ABD中,AD=10, 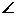 B=45°,
B=45°, 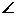 ADB=60°,
ADB=60°,
由正弦定理得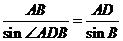 ,
,
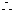 AB=
AB=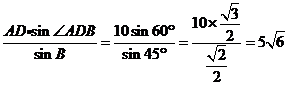
【点评】本题针对的是大多数考生,试题比较好理解,入题相对容易些,加上正余弦定理在我们平时学习中学生 也常用到。所以做这一类题比较上手很容易得满分.
也常用到。所以做这一类题比较上手很容易得满分.
18.(本小题满分12分)
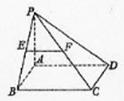
如图,在四棱锥P—ABCD中,底面ABCD是矩形,PA⊥平面ABCD,AP=AB,BP=BC=2,E,F分别是PB,PC 的中点.
的中点.
(Ⅰ)证明:EF∥平面PAD;
(Ⅱ)求三棱锥E—ABC的体积V.
【命题意图】本题主 要考查立体几何中点线面位置关系,并以我们熟悉的四棱锥为载体,尽管侧重推理和运算,但所用知识点不多,运算也不麻烦,对于大多考生来说还是一道送分题.
要考查立体几何中点线面位置关系,并以我们熟悉的四棱锥为载体,尽管侧重推理和运算,但所用知识点不多,运算也不麻烦,对于大多考生来说还是一道送分题.
【参考答案】 解: (Ⅰ) 在△PBC中,E,F分别是PB,PC的中点,∴EF∥BC.
又BC∥AD,∴ EF∥AD,
又∵AD 平面PAD,EF
平面PAD,EF 平面PAD,
平面PAD,
∴EF∥平面PAD.
(Ⅱ)连接AE,AC,EC,过E作EG∥PA交AB于点G,
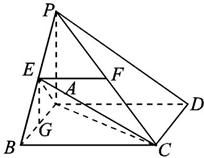
则EG⊥平面ABCD,且EG=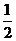 PA.
PA.
在△PAB中,AP=AB,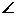 PAB=90°,BP=2,∴AP=AB=
PAB=90°,BP=2,∴AP=AB=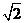 ,EG=
,EG=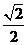 .
.
∴S△ABC=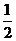 AB·BC=
AB·BC=
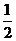 ×
×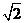 ×2=
×2=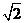 ,
,
∴VE-ABC=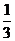 S△ABC·EG=
S△ABC·EG=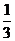 ×
×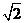 ×
×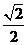 =
=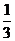 .
.
【点评】本题是我们常见的题型,相比平时那些求角及距离的题要容易的多,并且所考知识点不多运算也不麻烦,是一道基础题.












