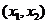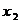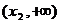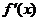(18)(本小题满分13分)
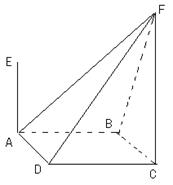
如图,四棱锥F-ABCD的底面ABCD是菱形,其对角线AC=2,BD=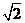 ,AE、CF都与平面ABCD垂直,AE=1,CF=2.
,AE、CF都与平面ABCD垂直,AE=1,CF=2.
(I)求二面角B-AF-D的大小;
(II)求四棱锥E-ABCD与四棱锥F-ABCD公共部分的体积.
本小题主要考查直线与直线、直线与平面、平面与平面的位置关系、相交平面所成二面角以及空间几何体的体积计算等知识,考查空间想象能力和推理论证能力、利用综合法或向量法解决立体几何问题的能力。本小题满分13分。
解:(I)(综合法)连接AC、BD交于菱形的中心O,过O作OG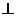 AF,
AF,
G为垂足。连接BG、DG。由BD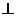 AC,BD
AC,BD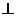 CF得BD
CF得BD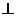 平面ACF,故BD
平面ACF,故BD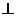 AF。
AF。
于是AF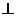 平面BGD,所以BG
平面BGD,所以BG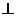 AF,DG
AF,DG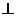 AF,
AF,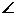 BGD为二面角B-AF-D 的平面角。
BGD为二面角B-AF-D 的平面角。
由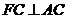 ,
, 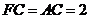 ,得
,得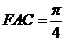 ,
,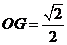


由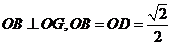 ,得
,得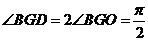
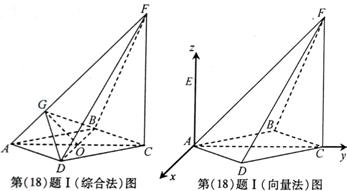
(向量法)以A为坐标原点,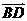 、
、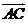 、
、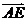 方向分别为x轴、y轴、z轴的正方向建立空间直角坐标系(如图)
方向分别为x轴、y轴、z轴的正方向建立空间直角坐标系(如图)
设平面ABF的法向量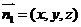 ,则由
,则由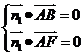 得
得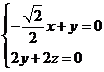
令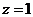 ,得
,得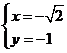 ,
,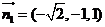
同理,可求得平面ADF的法向量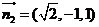 。
。

由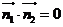 知,平面ABF与平面ADF垂直,
知,平面ABF与平面ADF垂直,
二面角B-AF-D的大小等于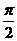 。
。
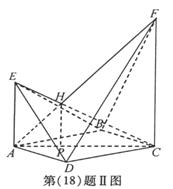
(II)连EB、EC、ED,设直线AF与直线CE相交于点H,则四棱锥E-ABCD与四棱锥F-ABCD的公共部分为四棱锥H-ABCD。
过H作HP⊥平面ABCD,P为垂足。
因为EA⊥平面ABCD,FC⊥平面ABCD,,所以平面ACFE⊥平面ABCD,从而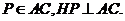
由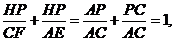 得
得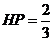 。
。
又因为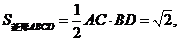


故四棱锥H-ABCD的体积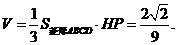
(19)(本小题满分12分)
已知函数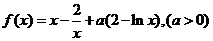 ,讨论
,讨论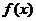 的单调性.
的单调性.
本小题主要考查函数的定义域、利用导数等知识研究函数的单调性,考查分类讨论的思想方法和运算求解的能力。本小题满分12分。
解: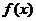 的定义域是(0,+
的定义域是(0,+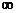 ),
),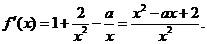
设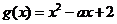 ,二次方程
,二次方程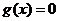 的判别式
的判别式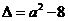 .
.
① 当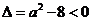 ,即
,即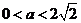 时,对一切
时,对一切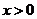 都有
都有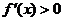 ,此时
,此时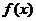 在
在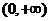 上是增函数。
上是增函数。
② 当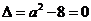 ,即
,即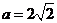 时,仅对
时,仅对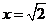 有
有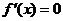 ,对其余的
,对其余的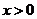 都有
都有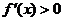 ,此时
,此时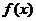 在
在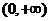 上也是增函数。
上也是增函数。

③ 当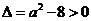 ,即
,即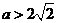 时,
时,
方程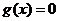 有两个不同的实根
有两个不同的实根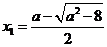 ,
,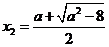 ,
,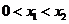 .
.
|
|
|
|
|
|
| + | 0 | _ | 0 | + |
| 单调递增 | 极大 | 单调递减 | 极小 | 单调递增 |
此时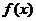 在
在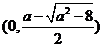 上单调递增, 在
上单调递增, 在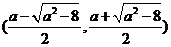 是上单调递减, 在
是上单调递减, 在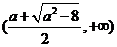 上单调递增.
上单调递增.
(20)(本小题满分13分)
点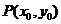 在椭圆
在椭圆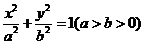 上,
上,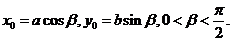 直线
直线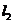 与直线
与直线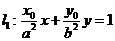 垂直,O为坐标原点,直线OP的倾斜角为
垂直,O为坐标原点,直线OP的倾斜角为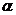 ,直线
,直线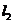 的倾斜角为
的倾斜角为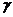 .
.
(I)证明: 点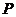 是椭圆
是椭圆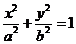 与直线
与直线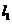 的唯一交点;
的唯一交点;

(II)证明: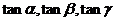 构成等比数列.
构成等比数列.
解:本小题主要考查直线和椭圆的标准方程和参数方程,直线和曲线的几何性质,等比数列等基础知识。考查综合运用知识分析问题、解决问题的能力。本小题满分13分。
解:(I)(方法一)由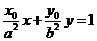 得
得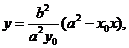 代入椭圆
代入椭圆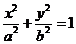 ,
,
得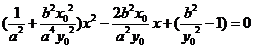 .
.
将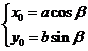 代入上式,得
代入上式,得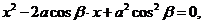 从而
从而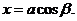
因此,方程组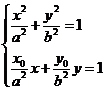 有唯一解
有唯一解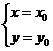 ,即直线
,即直线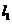 与椭圆有唯一交点P.
与椭圆有唯一交点P.

(方法二)显然P是椭圆与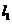 的交点,若Q
的交点,若Q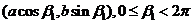 是椭圆与
是椭圆与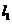 的交点,代入
的交点,代入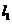 的方程
的方程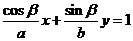 ,得
,得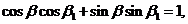
即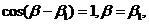 故P与Q重合。
故P与Q重合。
(方法三)在第一象限内,由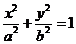 可得
可得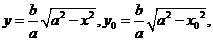
椭圆在点P处的切线斜率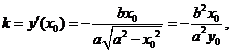
切线方程为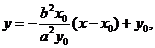 即
即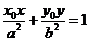 。
。
因此,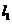 就是椭圆在点P处的切线。
就是椭圆在点P处的切线。
根据椭圆切线的性质,P是椭圆与直线 的唯一交点。
的唯一交点。
(II)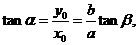
 的斜率为
的斜率为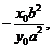
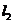 的斜率为
的斜率为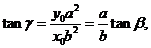
由此得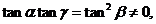
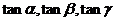 构成等比数列。
构成等比数列。
(21)(本小题满分13分)
首项为正数的数列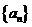 满足
满足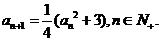


(I)证明:若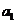 为奇数,则对一切
为奇数,则对一切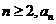 都是奇数;
都是奇数;
(II)若对一切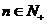 都有
都有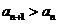 ,求
,求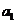 的取值范围.
的取值范围.
解:本小题主要考查数列、数学归纳法和不等式的有关知识,考查推理论证、抽象概括、运算求解和探究能力,考查学生是否具有审慎思维的习惯和一定的数学视野。本小题满分13分。
解:(I)已知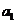 是奇数,假设
是奇数,假设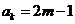 是奇数,其中
是奇数,其中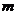 为正整数,
为正整数,
则由递推关系得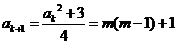 是奇数。
是奇数。

根据数学归纳法,对任何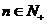 ,
,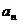 都是奇数。
都是奇数。
(II)(方法一)由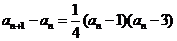 知,
知,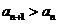 当且仅当
当且仅当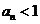 或
或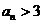 。
。
另一方面,若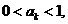 则
则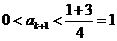 ;若
;若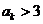 ,则
,则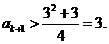
根据数学归纳法,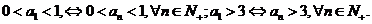
综合所述,对一切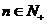 都有
都有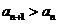 的充要条件是
的充要条件是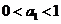 或
或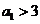 。
。
(方法二)由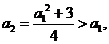 得
得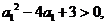 于是
于是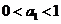 或
或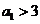 。
。
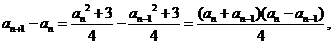


因为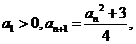 所以所有的
所以所有的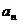 均大于0,因此
均大于0,因此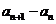 与
与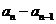 同号。
同号。
根据数学归纳法,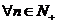 ,
,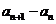 与
与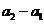 同号。
同号。

因此,对一切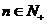 都有
都有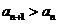 的充要条件是
的充要条件是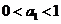 或
或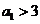 。
。