20 (本小题满分13分)
已知椭圆C的中心在原点,焦点在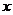 轴上,以两个焦点和短轴的两个端点为顶点的圆边形是一个面积为8的正方形(记为Q)
轴上,以两个焦点和短轴的两个端点为顶点的圆边形是一个面积为8的正方形(记为Q)
(1)求椭圆C的方程:

(2)设点P是椭圆C的左准线与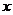 轴的交点,过点P的直线L与椭圆C相交于M.N两点,当线段MN的中点落在正方形Q内(包括边界)时,求直线L的斜率的取值范围。
轴的交点,过点P的直线L与椭圆C相交于M.N两点,当线段MN的中点落在正方形Q内(包括边界)时,求直线L的斜率的取值范围。
解 (1) 依题意,设椭圆C的方程为 焦距为
焦距为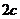 ,由题设条件知,
,由题设条件知,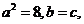 所以
所以 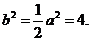 故椭圆C的方程式为
故椭圆C的方程式为


(3)椭圆C的左准线方程为 所以点P的坐标
所以点P的坐标 ,显然直线
,显然直线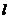 的斜率
的斜率 存在,所以直线
存在,所以直线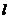 的方程为
的方程为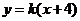 。
。

如图,设点M,N的左边分别为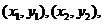 线段MN的中点G
线段MN的中点G ,
,
由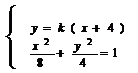 得
得
 ……①
……①
由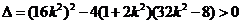 解得
解得 ……②
……②
因为 是方程①的两根,所以
是方程①的两根,所以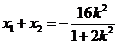 ,于是
,于是

 =
= ,
,


因为

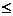 0,所以点G不可能在
0,所以点G不可能在 轴的右边,有直线
轴的右边,有直线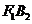 ,
,
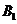 方程分
方程分
别为 所以点
所以点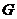 在正方形
在正方形 内(包括边界)的充要条件为
内(包括边界)的充要条件为

既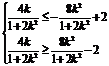 亦即
亦即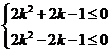


解得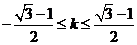 ,此时②也成立
,此时②也成立
故直线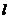 斜率的取值范围是[
斜率的取值范围是[ ,
, )
)
21.(本小题满分13分)
对于数列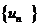 若存在常数M>0,对任意的
若存在常数M>0,对任意的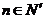 ,恒有
,恒有
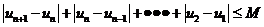


则称数列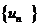 为
为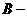 数列
数列
(I) 首项为1,公比为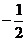 的等比数列是否为B-数列?请说明理由;
的等比数列是否为B-数列?请说明理由;
(II)设S 是数列
是数列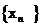 的前n项和。给出下列两组判断:
的前n项和。给出下列两组判断:
A组:①数列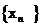 是B-数列。 ②数列
是B-数列。 ②数列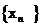 不是B-数列。
不是B-数列。
③数列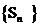 是B-数列。 ④数列
是B-数列。 ④数列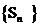 不是B-数列
不是B-数列
请以其中一组的一个论断条件,另一组中的一个论断为结论组成一个命题
判断所给命题的真假,并证明你的结论;
(Ⅲ)若数列{a }是B
}是B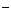 数列,证明:数列{a
数列,证明:数列{a }也是B
}也是B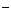 数列。
数列。

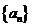 ,则
,则 ,于是
,于是



|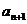 -
- 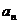 |+|
|+|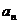 -
- |+…+|
|+…+| -
- |
|
=
=3× <3
<3
所以首项为1,公比为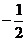 的等比数列是B-数列
的等比数列是B-数列

(Ⅱ)命题1:若数列{ }是B-数列,则数列{
}是B-数列,则数列{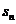 }是B-数列
}是B-数列
此命题为假命题
事实上设 =1,n
=1,n N,易知数列{
N,易知数列{ }是B-数列,但
}是B-数列,但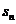 =n,
=n,
| -
- 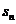 |+|
|+|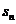 -
- |+…+|
|+…+| -
- |=n
|=n
由n有的任意性知,数列{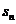 }不是B-数列。
}不是B-数列。
命题2:若数列{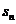 }是B-数列,则数列{
}是B-数列,则数列{ }不是B-数列。
}不是B-数列。
此命题为真命题。事实上,因为数列{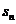 }是B-数列,所以存在正数M,对任意的n
}是B-数列,所以存在正数M,对任意的n N,有
N,有
| -
- 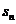 |+|
|+|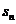 -
- |+…+|
|+…+| -
- |
|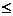 M
M

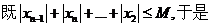

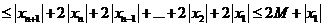
所以数列 是
是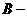 数列。
数列。
(注:按题中要求组成其它命题解答时,阐述解法)
③若数列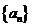 是
是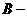 数列,则存在正数M,对任意的
数列,则存在正数M,对任意的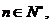 有
有

因为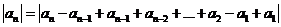
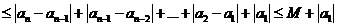
 ,则有
,则有

因此 
故数列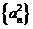 是
是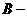 数列
数列













