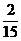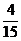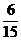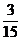18.(本小题满分12分)
某人在如图4所示的直角边长为4米的三角形地块的每个格点(指纵、横的交叉点记忆三角形的顶点)处都种了一株相同品种的作物。根据历年的种植经验,一株该种作物的年收获量Y(单位:kg)与它的“相近”作物株数X之间的关系如下表所示:
X | 1 | 2 | 3 | 4 |
Y | 51 | 48 | 45 | 42 |
这里,两株作物“相近”是指它们之间的直线距离不超过1米。
(I)从三角形地块的内部和边界上分别随机选取一株作物,求它们恰好“相近”的概率;
(II)从所种作物中随机选取一株,求它的年收获量的分布列与数学期望。
【答案】 (Ⅰ) 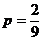 (Ⅱ)
(Ⅱ)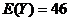
【解析】 (Ⅰ) 由图知,三角形边界共有12个格点,内部共有3个格点.
从三角形上顶点按逆时针方向开始,分别有0,0,1,1,0,1,1,0,0,1,2,1对格点,共8对格点恰好“相近”。
所以,从三角形地块的内部和边界上分别随机选取一株作物,它们恰好“相近”的概率
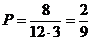
(Ⅱ)三角形共有15个格点。
与周围格点的距离不超过1米的格点数都是1个的格点有2个,坐标分别为(4,0),(0,4)。
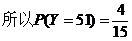
与周围格点的距离不超过1米的格点数都是2个的格点有4个,坐标分别为(0,0), (1,3), (2,2),(3,1)。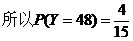
与周围格点的距离不超过1米的格点数都是3个的格点有6个,坐标分别为(1,0), (2,0), (3,0),(0,1,) ,(0,2),(0,3,)。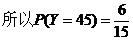
与周围格点的距离不超过1米的格点数都是4个的格点有3个,坐标分别为(1,1), (1,2), (2,1)。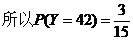
如下表所示:
X | 1 | 2 | 3 | 4 |
Y | 51 | 48 | 45 | 42 |
频数 | 2 | 4 | 6 | 3 |
概率P |
|
|
|
|
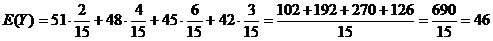
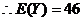 . (完)
. (完)
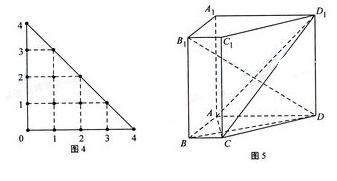
19.(本小题满分12分)如图5,在直棱柱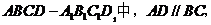
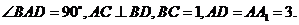
(I)证明: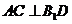 ;
;
(II)求直线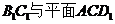 所成角的正弦值。
所成角的正弦值。
【答案】 (Ⅰ) 见下 (Ⅱ)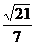
【解析】 (Ⅰ) 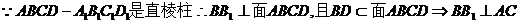
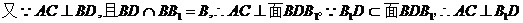 . (证毕)
. (证毕)
(Ⅱ)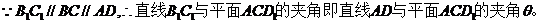
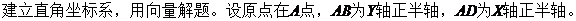
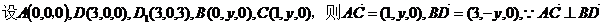


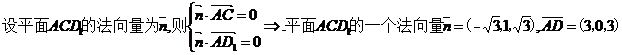
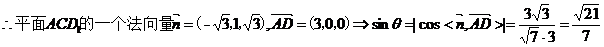
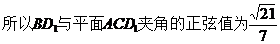 。(完)
。(完)
20.(本小题满分13分)
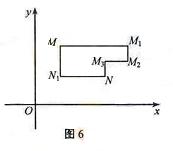
在平面直角坐标系xOy中,将从点M出发沿纵、横方向到达点N的任一路径成为M到N的一条“L路径”。如图6所示的路径 都是M到N的“L路径”。某地有三个新建的居民区,分别位于平面xOy内三点
都是M到N的“L路径”。某地有三个新建的居民区,分别位于平面xOy内三点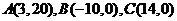 处。现计划在x轴上方区域(包含x轴)内的某一点P处修建一个文化中心。
处。现计划在x轴上方区域(包含x轴)内的某一点P处修建一个文化中心。
(I)写出点P到居民区A的“L路径”长度最小值的表达式(不要求证明);
(II)若以原点O为圆心,半径为1的圆的内部是保护区,“L路径”不能进入保护区,请确定点P的位置,使其到三个居民区的“L路径”长度值和最小。
【答案】 (Ⅰ)d= |x – 3| + |y – 20|,
(Ⅱ)当点P(x,y)满足P(3,1)时, 其到三个居民区的“L路径”长度值和最小为45
【解析】 
(Ⅰ) 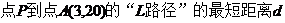 ,
,
 ,其中
,其中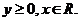
(Ⅱ)本问考查分析解决应用问题的能力,以及绝对值的基本知识。
点P到A,B,C三点的“L路径”长度之和的最小值d = 水平距离之和的最小值h + 垂直距离之和的最小值v。且h和v互不影响。显然当y=1时,v = 20+1=21;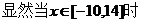 ,水平距离之和h=x – (-10) + 14 – x + |x-3|
,水平距离之和h=x – (-10) + 14 – x + |x-3| 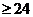 ,且当x=3时,h=24.因此,当P(3,1)时,d=21+24=45.
,且当x=3时,h=24.因此,当P(3,1)时,d=21+24=45.
所以,当点P(x,y)满足P(3,1)时,点P到A,B,C三点的“L路径”长度之和d的最小值为45.
21.(本小题满分13分)
过抛物线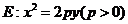 的焦点F作斜率分别为
的焦点F作斜率分别为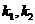 的两条不同的直线
的两条不同的直线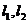 ,且
,且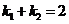 ,
,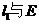 相交于点A,B,
相交于点A,B,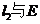 相交于点C,D。以AB,CD为直径的圆M,圆N(M,N为圆心)的公共弦所在的直线记为
相交于点C,D。以AB,CD为直径的圆M,圆N(M,N为圆心)的公共弦所在的直线记为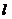 。
。
(I)若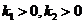 ,证明;
,证明;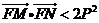 ;
;
(II)若点M到直线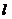 的距离的最小值为
的距离的最小值为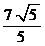 ,求抛物线E的方程。
,求抛物线E的方程。
【答案】 (Ⅰ) 见下 (Ⅱ)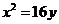
【解析】 (Ⅰ) 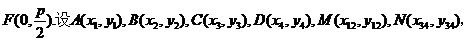

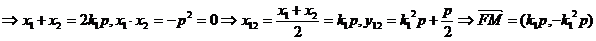
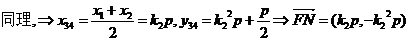 .
.
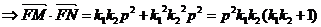
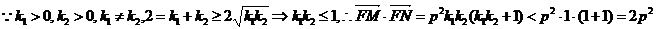 所以,
所以,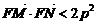 成立. (证毕)
成立. (证毕)
(Ⅱ)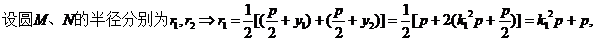
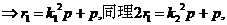
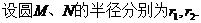 则
则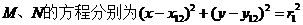 ,
,
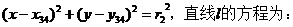
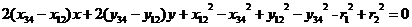 .
.
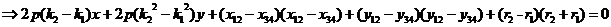
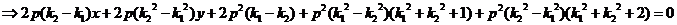
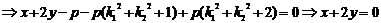
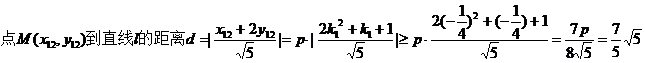
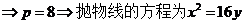 .(完)
.(完)
22.(本小题满分13分)
已知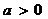 ,函数
,函数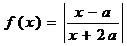 。
。
(I);记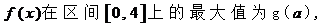 求
求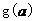 的表达式;
的表达式;
(II)是否存在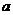 ,使函数
,使函数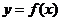 在区间
在区间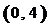 内的图像上存在两点,在该两点处的切线相互垂直?若存在,求
内的图像上存在两点,在该两点处的切线相互垂直?若存在,求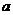 的取值范围;若不存在,请说明理由。
的取值范围;若不存在,请说明理由。
【答案】 (Ⅰ) 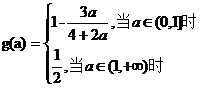 (Ⅱ)
(Ⅱ)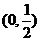
【解析】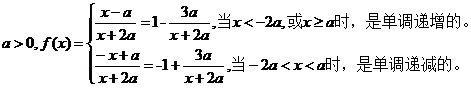
(Ⅰ)

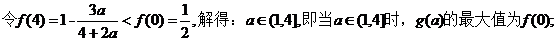
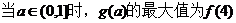
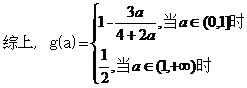
(II)由前知,y=f(x)的图像是由两段反比例函数的图像组成的。因此,若在图像上存在两点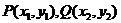 满足题目要求,则P,Q分别在两个图像上,且
满足题目要求,则P,Q分别在两个图像上,且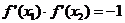 。
。
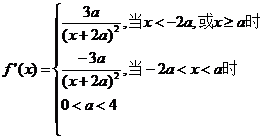
不妨设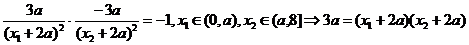
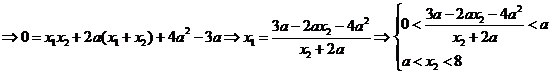
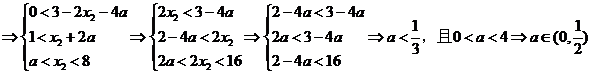
所以,当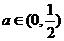 时,函数
时,函数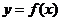 在区间
在区间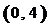 内的图像上存在两点,在该两点处的切线相互垂直.(完)
内的图像上存在两点,在该两点处的切线相互垂直.(完)