二、填空题共6小题,每小题5分,共30分。
9.在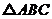 中,若
中,若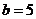 ,
,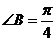 ,
,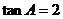 ,则
,则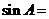 _______,
_______,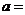 ______.
______.
【答案】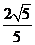
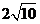
【解析】由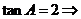
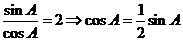 ,又
,又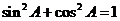 所以
所以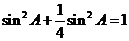 解得
解得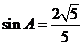 ,正弦定理得
,正弦定理得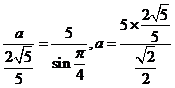 则
则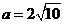 。
。
10.已知向量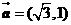 ,
,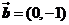 ,
,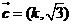 ,若
,若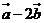 与
与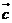 共线,则
共线,则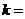 ________.
________.
【答案】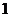
【解析】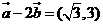 由
由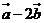 与
与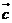 共线得
共线得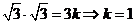
11.在等比数列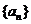 中,若
中,若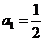 ,
,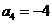 ,则公比
,则公比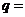 ________;
________;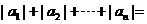 ________.
________.
【答案】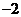
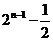
【解析】由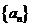 是等比数列得
是等比数列得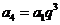 ,又
,又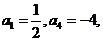 所以
所以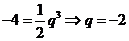 ,
,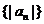 是以
是以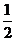 为首项,以2为公比的等比数列,
为首项,以2为公比的等比数列,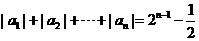 。
。
12.用数字2,3组成四位数,且数字2,3至少都出现一次,这样的四位数共有______个(用数字作答)
【答案】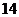
【解析】个数为
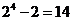 。
。
13.已知函数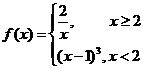 ,若关于x的方程
,若关于x的方程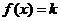 有两个不同的实根,则实数k的取值范围是________.
有两个不同的实根,则实数k的取值范围是________.
【答案】(0,1)
【解析】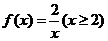
 单调递减且值域为(0,1],
单调递减且值域为(0,1],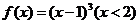 单调递增且值域为
单调递增且值域为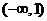 ,
,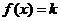 有两个不同的实根,则实数k的取值范围是(0,1)。
有两个不同的实根,则实数k的取值范围是(0,1)。
14.曲线C是平面内与两个定点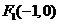 和
和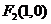 的距离的积等于常数
的距离的积等于常数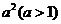 的点的轨迹,给出下列三个结论:①曲线C过坐标原点;②曲线C关于坐标原点对称;③若点P在曲线C上,则
的点的轨迹,给出下列三个结论:①曲线C过坐标原点;②曲线C关于坐标原点对称;③若点P在曲线C上,则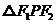 的面积不大于
的面积不大于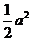 .其中,所有正确结论的序号是____________.
.其中,所有正确结论的序号是____________.
【答案】② ③
③
【解析】:①曲线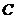 经过原点,这点不难验证是错误的,如果经过原点,即么
经过原点,这点不难验证是错误的,如果经过原点,即么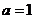 ,与条件不符;②曲线
,与条件不符;②曲线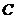 关于原点对称,这点显然正确,如果在某点处
关于原点对称,这点显然正确,如果在某点处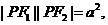 关于原点的对称点处也一定符合
关于原点的对称点处也一定符合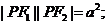 ③三角形
③三角形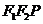 的面积
的面积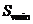
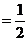
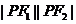
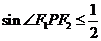
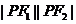 =
=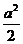
三、解答题共6小题,共80分。解答应写出文字说明,演算步骤或证明过程。
15.已知函数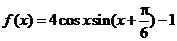 .
.
(1)求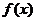 的最小正周期;
的最小正周期;
(2)求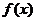 在区间
在区间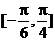 上的最大值和最小值。
上的最大值和最小值。
【解析】:(Ⅰ)因为
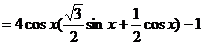
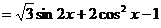
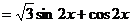
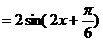 所以
所以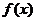 的最小正周期为
的最小正周期为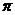
(Ⅱ)因为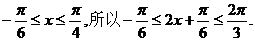 于是,当
于是,当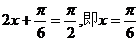 时,
时,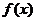 取得最大值2;当
取得最大值2;当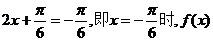 取得最小值—1.
取得最小值—1.












