16. (共14分)如图,在四棱锥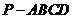 中,
中,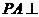 平面ABCD,底面ABCD是菱形,
平面ABCD,底面ABCD是菱形,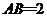 ,
,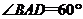 .
.
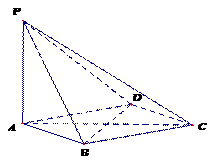
(1)求证: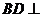 平面PAC;
平面PAC;
(2)若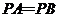 ,求PB与AC所成角的余弦值;
,求PB与AC所成角的余弦值;
(3)当平面PBC与平面PDC垂直时,求PA的长.
【解析】:证明:(Ⅰ)因为四边形ABCD是菱形,所以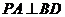 又因为
又因为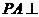 平面
平面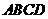 。所以
。所以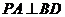 ,
,
所以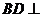 平面
平面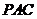 。
。
(Ⅱ) 设
设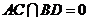 ,因为
,因为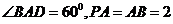
所以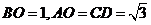 ,如图,以O为坐标原点,建立空间直角坐标系
,如图,以O为坐标原点,建立空间直角坐标系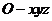 ,则
,则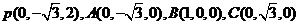 所
所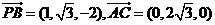 设
设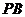 与
与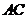 所成角为
所成角为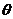 ,则
,则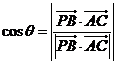
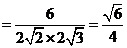
(Ⅲ)由(Ⅱ)知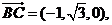 设
设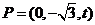
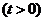 。则
。则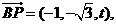 设平面
设平面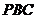 的法
的法
向量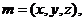 则
则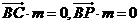 ,所以
,所以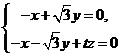 令
令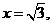 则
则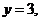
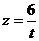 ,
,
所以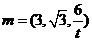 同理,平面
同理,平面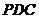 的法向量
的法向量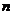
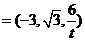 ,因为平面
,因为平面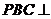
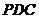 ,所以
,所以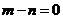 ,即
,即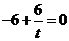 解得
解得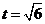 ,所以
,所以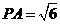
17.以下茎叶图记录了甲、乙两组各四名同学的植树棵数。乙组记录中有一个数据模糊,无法确认,
在图中以X表示。
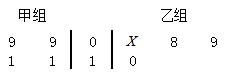
(1)如果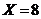 ,求乙组同学植树棵数的平均数和方差;
,求乙组同学植树棵数的平均数和方差;
(2)如果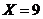 ,分别从甲、乙两组中随机选取一名同学,求这两名同学的植树总棵数Y的分布列和
,分别从甲、乙两组中随机选取一名同学,求这两名同学的植树总棵数Y的分布列和 数学期望。(注:方差
数学期望。(注:方差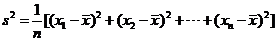 ,其中
,其中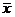 为
为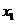 ,
,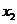 ,…,
,…,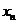 的平均数)
的平均数)
【解析】:(1)当X=8时,由茎叶图可知,乙组同学的植树棵数是:8,8,9,10,
所以平均数为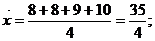
方差为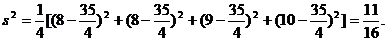
(Ⅱ)当 X=9时,由茎叶图可知,甲组同学的植树棵树是:9,9,1
X=9时,由茎叶图可知,甲组同学的植树棵树是:9,9,1 1,11;乙组同学的植树棵数是:9,8,9,10。分别从甲、乙两组中随机选取一名同学,共有4×4=16种可能的结果,这两名同学植树总棵数Y的可能取值为17,18,19,20,21事件“Y=17”等价于“甲组选出的同学植树9棵,乙组选出的同学植树8棵”所以该事件有2种可能的结果,因此P(Y=17)=
1,11;乙组同学的植树棵数是:9,8,9,10。分别从甲、乙两组中随机选取一名同学,共有4×4=16种可能的结果,这两名同学植树总棵数Y的可能取值为17,18,19,20,21事件“Y=17”等价于“甲组选出的同学植树9棵,乙组选出的同学植树8棵”所以该事件有2种可能的结果,因此P(Y=17)=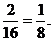
同理可得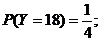
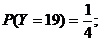
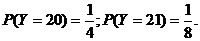
所以随机变量Y的分布列为:
Y | 17 | 18 | 19 | 20 | 21 |
P |
|
|
|
|
|
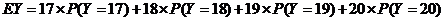
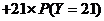
=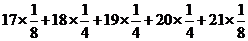 =19
=19
18.已知函数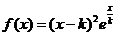 .(1)求
.(1)求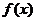 的单调区间;(2)若对
的单调区间;(2)若对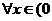 ,
,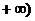 ,都有
,都有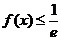 ,求
,求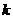 的取值范围。
的取值范围。
【解析】:(Ⅰ)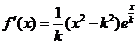 ,令
,令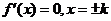 ,当
,当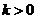 时,
时,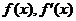 的情况如下:
的情况如下:
|
|
|
|
|
|
| + | 0 |
| 0 | + |
|
|
| 0 |
所以,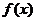 的单调递增区间是
的单调递增区间是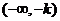 和
和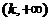 :单调递减区间是
:单调递减区间是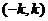 ,当
,当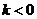 时,
时,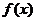 与
与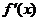 的情况如下
的情况如下 :
:
|
|
|
|
|
|
|
| 0 | + | 0 |
|
|
| 0 |
|
所以,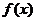 的单调递减区间是
的单调递减区间是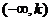 和
和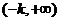 :单调递减区间是
:单调递减区间是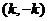 。
。
(Ⅱ)当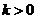 时,因为
时,因为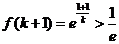 ,所以不会有
,所以不会有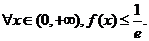 当
当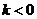 时,由(Ⅰ)知
时,由(Ⅰ)知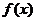 在
在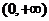 上的最大值是
上的最大值是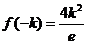 所以
所以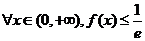 等价于
等价于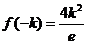
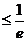 , 解得
, 解得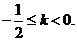 故当
故当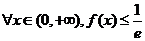 时,
时,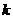 的取值范围是[
的取值范围是[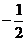 ,0]。
,0]。
19.已知椭圆G: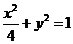 ,过点(m,0)作圆
,过点(m,0)作圆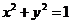 的切线l交椭圆G于A,B两点。
的切线l交椭圆G于A,B两点。
(1)求椭圆G的焦点坐标和离心率;(2)将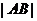 表示为m
表示为m 的函数,并求
的函数,并求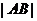 的最大值。
的最大值。
【解析】::(Ⅰ)由已知得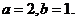 所以
所以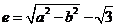 所以椭圆
所以椭圆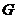 的焦点坐标为
的焦点坐标为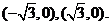 ,离心率为
,离心率为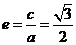
(Ⅱ)(Ⅱ)由题意知,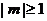 .当
.当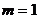 时,切线l的方程
时,切线l的方程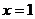 ,点A、B的坐标分别为
,点A、B的坐标分别为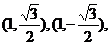 此时
此时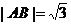 当m=-1时,同理可得
当m=-1时,同理可得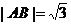
当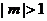 时,设切线l的方程为
时,设切线l的方程为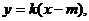 由
由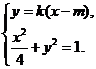
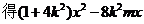
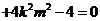 设A、B两点的坐标分别为
设A、B两点的坐标分别为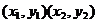 ,则
,则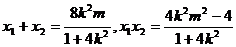 又由l与圆
又由l与圆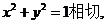
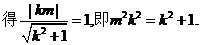 所以
所以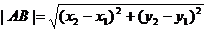
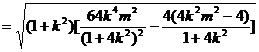
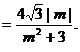 由于当
由于当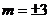 时,
时,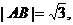
所以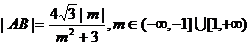 .因为
.因为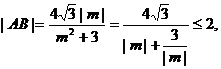
且当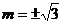 时,|AB|=2,所以|AB|的最大值为2
时,|AB|=2,所以|AB|的最大值为2
20.若数列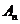 :
: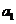 ,
,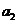 ,…,
,…,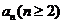 满足
满足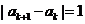 (
(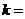
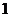 ,2,…,
,2,…,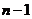 ),则称
),则称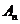 为E数列。记
为E数列。记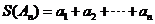 .(1)写出一个满足
.(1)写出一个满足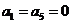 ,且
,且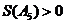 的E数列
的E数列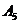 ;(2)若
;(2)若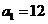 ,
,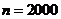 ,证明:E数列
,证明:E数列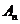 是递增数列的充要条件是
是递增数列的充要条件是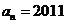 ;(3)对任意给定的整数
;(3)对任意给定的整数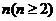 ,是否存在首项为0的E数列
,是否存在首项为0的E数列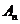 ,使得
,使得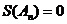 ?如果存在,写出一个满足条件的E数列
?如果存在,写出一个满足条件的E数列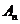 ;如果不存在,说明理由。
;如果不存在,说明理由。
 【解析】:(Ⅰ)0,1,2,1,0是一具满足条件的E数列A5。
【解析】:(Ⅰ)0,1,2,1,0是一具满足条件的E数列A5。
(答案不唯一,0,1,0,1,0也是一个满足条件的E的数列A5)
(Ⅱ)必要性:因为E数列A5是递增数列,所以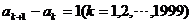 .所以A5是首项为12,公差为1的等差数列.所以a2000=12+(2000—1)×1=2011.充分性,由于a2000—a1000
.所以A5是首项为12,公差为1的等差数列.所以a2000=12+(2000—1)×1=2011.充分性,由于a2000—a1000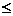 1,a2000—a1000
1,a2000—a1000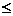 1……a2—a1
1……a2—a1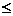 1所以a2000—a
1所以a2000—a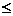 19999,即a2000
19999,即a2000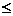 a1+1999.又因为a1=12,a2000=2011,所以a2000=a1+1999.故
a1+1999.又因为a1=12,a2000=2011,所以a2000=a1+1999.故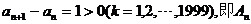 是递增数列.综上,结论得证。
是递增数列.综上,结论得证。