第Ⅱ卷

二．填空题：本大题共5小题，每小题5分，共25分。

11.若曲线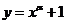（α∈R）在点（1，2）处的切线经过坐标原点，则α= 。

[答案]：2

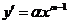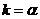[解析]：，则，故切线方程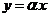过点（1，2）解得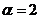

12.某住宅小区计划植树不少于100棵，若第一天植2棵，以后每天植树的棵树是前一天的2倍，则需要的最少天数n（n∈N*）等于 。

[答案]：6

[解析]：直接计算2+4+8+16+32+64＝128得n=6, 或解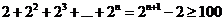得n为6.

13设f（x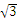）=sin3x+cos3x，若对任意实数x都有|f（x）|≤a，则实数a的取值范围是 。

[答案]：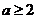

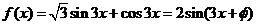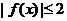[解析]：得故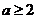

14.若圆C经过坐标原点和点（4，0），且与直线y=1相切，则圆C的方程是 。

[答案]：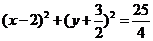

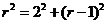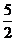[解析]：设圆心坐标为（x，y）,半径为r，则x=2,又故r=，则。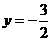

15.如图，正方体的底面与正四面体的底面在同一平面α上，且AB//CD,则直线EF与正方体的六个面所在的平面相交的平面个数为 。

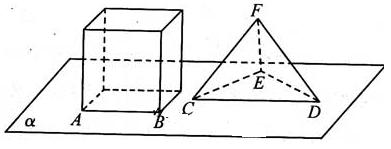
[答案]：4

[解析]：设CD的中点为M，连结EM，FM易证平面EFM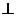平面α，则EF与平面α平行，不会相交，故EF只与其余四个面相交。

三．解答题：本大题共6小题，共75分。解答应写出文字说明，证明过程或演算步骤。

16.（本小题满分12分）　正项数列｛an｝满足。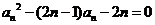

求数列｛an｝的通项公式an；

令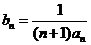，求数列｛bn｝的前n项和Tn。

[解析]：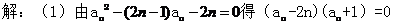

由于｛an｝是正项数列，则。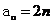

（2）由（1）知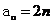，故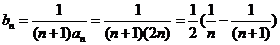

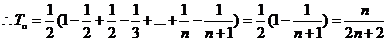
17.（本小题满分12分）

在△ABC中，角A，B，C的对边分别为a，b，c，已知sinAsinB+sinBsinC+cos2B=1.

求证：a，b，c成等差数列；

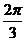
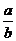若C=，求的值。

[解析]：（1）由已知得sinAsinB+sinBsinC+1-2sin2B=1.故sinAsinB+sinBsinC=2sin2B因为sinB不为0，所以sinA+sinC=2sinB再由正弦定理得a+c=2b,所以a，b，c成等差数列

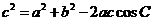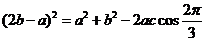（2）由余弦定理知得化简得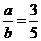

18．（本小题满分12分）

小波已游戏方式决定是去打球、唱歌还是去下棋。游戏规则为以O为起点，再从A1,A2,A3,A4,A5,A6（如图）这6个点中任取两点分别为终点得到两个向量，记住这两个向量的数量积为X，若X>0就去打球，若X=0就去唱歌，若X<0就去下棋

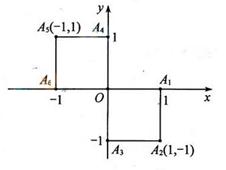
写出数量积X的所有可能取值

分别求小波去下棋的概率和不去唱歌的概率

解：（1） x 的所有可能取值为-2 ，-1 ，0， 1。

（2）数量积为-2的只有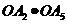一种

数量积为-1的有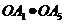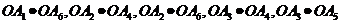，六种

数量积为0的有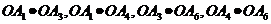四种

数量积为1的有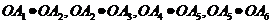四种

故所有可能的情况共有15种。

所以小波去下棋的概率为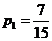

因为去唱歌的概率为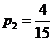，所以小波不去唱歌的概率

点击此处下载文档(rar格式，379.37KB)