三、解答题;本大题共6小题,共75分。解答应写出文字说明、证明过程或演算步骤。
16.(本小题满分12分)
已知函数 f(x)=
f(x)=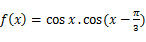
(1) 求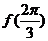 的值;
的值;
(2) 求使 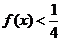 成立的x的取值集合
成立的x的取值集合
【答案】 (1) 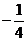 (2)
(2) 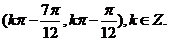
【解析】 (1) 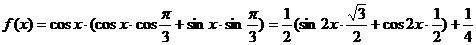
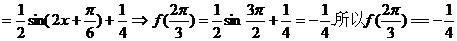 。
。
(3) 由(1)知,
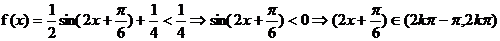
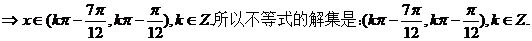
17.(本小题满分12分)
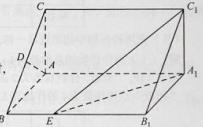
如图2.在直菱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=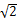 ,AA1=3,D是BC的中点,点E在菱BB1上运动。
,AA1=3,D是BC的中点,点E在菱BB1上运动。
(I) 证明:AD⊥C1E;
(II)当异面直线AC,C1E 所成的角为60°时,
求三菱子C1-A2B1E的体积
【答案】 (Ⅰ) 见下 (Ⅱ)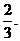
【解析】 (Ⅰ) 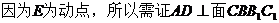 .
.
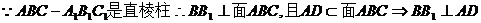
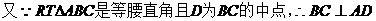 .
.
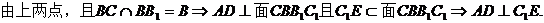 (证毕)
(证毕)
(Ⅱ)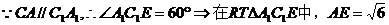 .
.
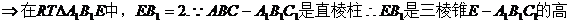 .
.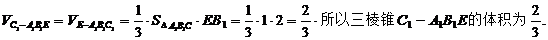
18.(本小题满分12分)
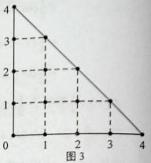
某人在如图3所示的直角边长为4米的三角形地块的每个格点(指纵、横直线的交叉点以及三角形的顶点)处都种了一株相同品种的作物。根据历年的种植经验,一株该种作物的年收货量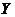 (单位:kg)与它的“相近”作物株数
(单位:kg)与它的“相近”作物株数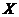 之间的关系如下表所示:
之间的关系如下表所示:

这里,两株作物“相近”是指它们之间的直线距离不超过1米。
(Ⅰ)完成下表,并求所种作物的平均年收获量;

(Ⅱ)在所种作物中随机选取一株,求它的年收获量至少为48kg的概率.
【答案】 (Ⅰ) 46 (Ⅱ)0.4
【解析】 (Ⅰ) 由图知,三角形中共有15个格点,
与周围格点的距离不超过1米的格点数都是1个的格点有2个,坐标分别为(4,0),(0,4)。
与周围格点的距离不超过1米的格点数都是2个的格点有4个,坐标分别为(0,0), (1,3), (2,2),(3,1)。
与周围格点的距离不超过1米的格点数都是3个的格点有6个,坐标分别为(1,0), (2,0), (3,0),(0,1,) ,(0,2),(0,3,)。
与周围格点的距离不超过1米的格点数都是4个的格点有3个,坐标分别为(1,1), (1,2), (2,1)。如下表所示:
Y | 51 | 48 | 45 | 42 |
频数 | 2 | 4 | 6 | 3 |
平均年收获量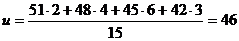 .
.
(Ⅱ)在15株中,年收获量至少为48kg的作物共有2+4=6个.
所以,15株中任选一个,它的年收获量至少为48k的概率P=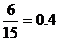 .
.
19.(本小题满分13分)
设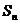 为数列{
为数列{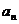 }的前项和,已知
}的前项和,已知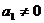 ,2
,2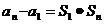 ,
,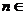 N
N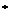
(Ⅰ)求 ,
,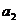 ,并求数列{
,并求数列{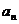 }的通项公式;
}的通项公式;
(Ⅱ)求数列{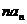 }的前
}的前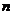 项和。
项和。
【答案】 (Ⅰ) 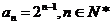 (Ⅱ)
(Ⅱ)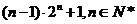
【解析】 (Ⅰ) 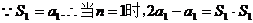
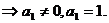
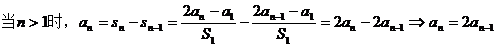 -
-
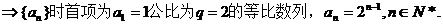
(Ⅱ)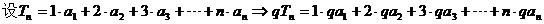
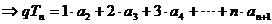
上式左右错位相减:
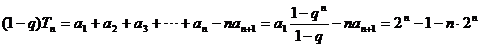
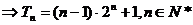 。
。
20.(本小题满分13分)
已知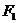 ,
,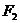 分别是椭圆
分别是椭圆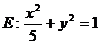 的左、右焦点
的左、右焦点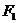 ,
,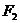 关于直线
关于直线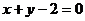 的对称点是圆
的对称点是圆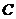 的一条直径的两个端点。
的一条直径的两个端点。
(Ⅰ)求圆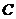 的方程;
的方程;
(Ⅱ)设过点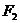 的直线
的直线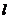 被椭圆
被椭圆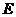 和圆
和圆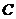 所截得的弦长分别为
所截得的弦长分别为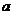 ,
,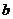 。当
。当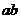 最大时,求直线
最大时,求直线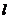 的方程。
的方程。
【答案】 (Ⅰ) 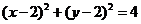 (Ⅱ)
(Ⅱ)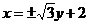
【解析】 (Ⅰ) 先求圆C关于直线x + y – 2 = 0对称的圆D,由题知圆D的直径为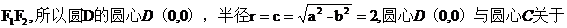 直线
直线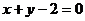 对称
对称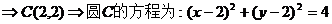 .
.
(Ⅱ)由(Ⅰ)知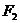 (2,0), ,据题可设直线
(2,0), ,据题可设直线 方程为: x = my +2,m∈R. 这时直线
方程为: x = my +2,m∈R. 这时直线 可被圆和椭圆截得2条弦,符合题意.
可被圆和椭圆截得2条弦,符合题意.
圆C: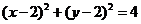 到直线
到直线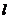 的距离
的距离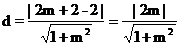 。
。
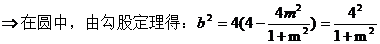 .
.
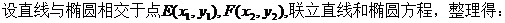
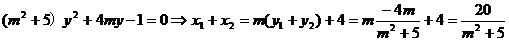
由椭圆的焦半径公式得: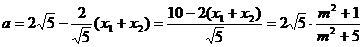
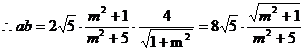 .
.
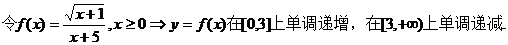

所以当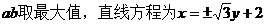
21.(本小题满分13分
已知函数f(x)=
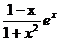 .
.
(Ⅰ)求f(x)的单调区间;
(Ⅱ)证明:当f(x1)=f(x2)(x1≠x2)时,x1+x2<0.
【答案】 (Ⅰ)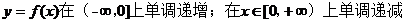 .
.
(Ⅱ)见下。
【解析】 (Ⅰ) 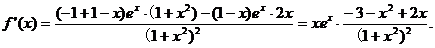
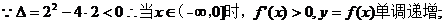
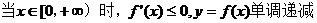 .
.
所以,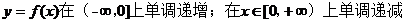 。
。
(Ⅱ)由(Ⅰ)知,只需要证明:当x>0时f(x) < f(-x)即可。
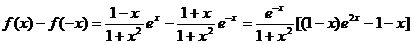 。
。
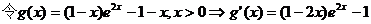 。
。
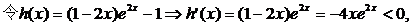
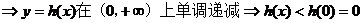
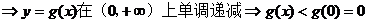
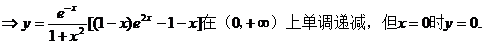
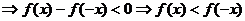
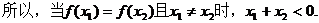 (证毕)
(证毕)












