三.解答题
(16)(本小题满分12分)
设函数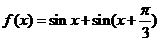 .
.
(Ⅰ)求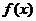 的最小值,并求使
的最小值,并求使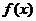 取得最小值的
取得最小值的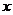 的集合;
的集合;
(Ⅱ)不画图,说明函数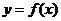 的图像可由
的图像可由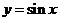 的图象经过怎样的变化得到.
的图象经过怎样的变化得到.
【解析】(1)
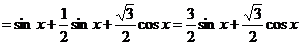
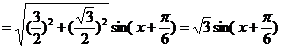
当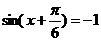 时,
时,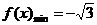 ,此时
,此时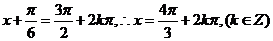
所以,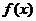 的最小值为
的最小值为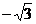 ,此时x 的集合
,此时x 的集合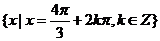 .
.
(2)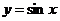 横坐标不变,纵坐标变为原来的
横坐标不变,纵坐标变为原来的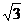 倍,得
倍,得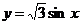 ;
;
然后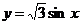 向左平移
向左平移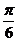 个单位,得
个单位,得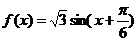
【考点定位】本题主要考查三角恒等变形、三角函数的图像及性质与三角函数图像的变换.考查逻辑推理和运算求解能力,中等难度.
(17)(本小题满分12分)
为调查甲、乙两校高三年级学生某次联考数学成绩情况,用简单随机抽样,从这两校中各抽取30名高三年级学生,以他们的数学成绩(百分制)作为样本,样本数据的茎叶图如下:
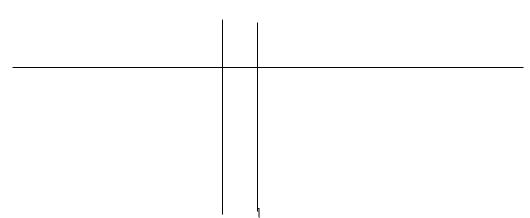
甲 乙
7 4 5
5 3 3 2 5 3 3 8
5 5 4 3 3 3 1 0 0 6 0 6 9 1 1 2 2 3 3 5
8 6 6 2 2 1 1 0 0 7 0 0 2 2 2 3 3 6 6 9
7 5 4 4 2 8 1 1 5 5 8
2 0 9 0
(Ⅰ)若甲校高三年级每位学生被抽取的概率为0.05,求甲校高三年级学生总人数,并估计甲校高三年级这次联考数学成绩的及格率(60分及60分以上为及格);
(Ⅱ)设甲、乙两校高三年级学生这次联考数学平均成绩分别为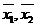 ,估计
,估计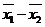 的值.
的值.
【解析】(1)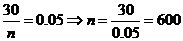

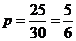
(2)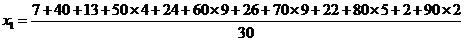
=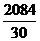
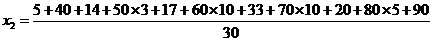
=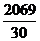
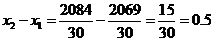
【考点定位】考查随机抽样与茎叶图等统计学基本知识,考查用样本估计总体的思想性以及数据分析处理能力.
(18)(本小题满分12分)
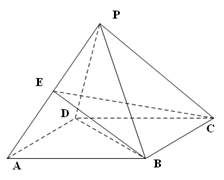
如图,四棱锥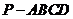 的底面
的底面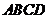 是边长为2的菱形,
是边长为2的菱形,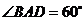 .已知
.已知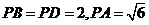 .
.
(Ⅰ)证明: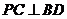
(Ⅱ)若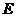 为
为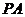 的中点,求三菱锥
的中点,求三菱锥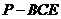 的体积.
的体积.
【解析】
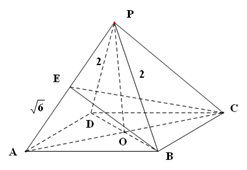
(1)证明:连接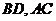 交于
交于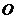 点
点
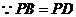
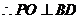
又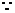
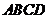 是菱形
是菱形 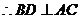
而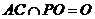
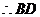 ⊥面
⊥面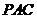
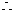
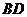 ⊥
⊥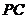
(2) 由(1)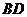 ⊥面
⊥面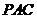
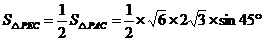 =
=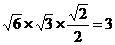
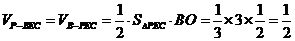
【考点定位】考查空间直线与直线,直线与平面的位置,.三棱锥体积等基础知识和基本技能,考查空间观念,推理论证能力和运算能力.
(19)(本小题满分13分)
设数列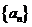 满足
满足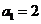 ,
,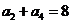 ,且对任意
,且对任意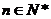 ,函数
,函数 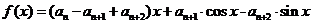 满足
满足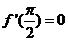
(Ⅰ)求数列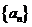 的通项公式;
的通项公式;
(Ⅱ)若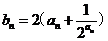 ,求数列
,求数列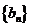 的前
的前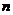 项和
项和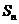 .
.
【解析】
由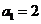
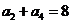
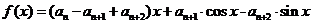
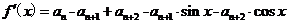
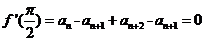
所以,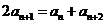
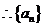 是等差数列.
是等差数列.
而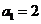
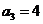
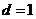
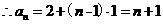
(2)
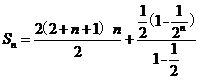
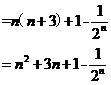
【考点定位】考查函数的求导法则和求导公式,等差、等比数列的性质和数列基本量的求解.并考查逻辑推理能力和运算能力.
(20)(本小题满分13分)
设函数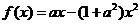 ,其中
,其中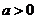 ,区间
,区间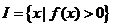 .
.
(Ⅰ)求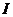 的长度(注:区间
的长度(注:区间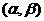 的长度定义为
的长度定义为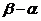 ;
;
(Ⅱ)给定常数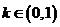 ,当
,当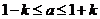 时,求
时,求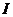 长度的最小值.
长度的最小值.
【解析】
(1)令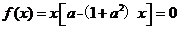
解得 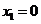
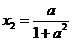
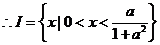
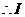 的长度
的长度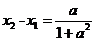
(2) 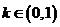 则
则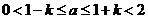
由 (1)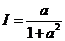
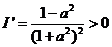 ,则
,则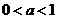
故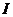 关于
关于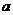 在
在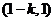 上单调递增,在
上单调递增,在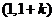 上单调递减.
上单调递减.
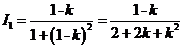
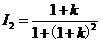
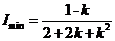
【考点定位】考查二次不等式的求解,以及导数的计算和应用,并考查分类讨论思想和综合运用数学知识解决问题的能力.
(21)(本小题满分13分)
已知椭圆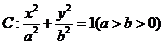 的焦距为4,且过点
的焦距为4,且过点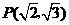 .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设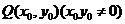 为椭圆
为椭圆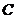 上一点,过点
上一点,过点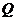 作
作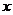 轴的垂线,垂足为
轴的垂线,垂足为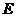 。取点
。取点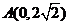 ,连接
,连接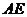 ,过点
,过点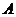 作
作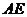 的垂线交
的垂线交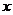 轴于点
轴于点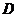 。点
。点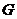 是点
是点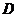 关于
关于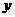 轴的对称点,作直线
轴的对称点,作直线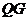 ,问这样作出的直线
,问这样作出的直线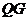 是否与椭圆C一定有唯一的公共点?并说明理由.
是否与椭圆C一定有唯一的公共点?并说明理由.
【解析】
(1)因为椭圆过点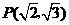
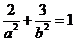 且
且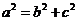
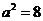
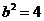
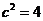 椭圆C的方程是
椭圆C的方程是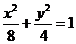
(2)
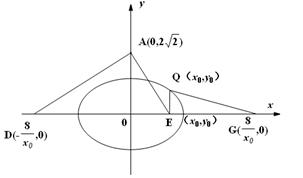
由题意,各点的坐标如上图所示,
则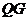 的直线方程:
的直线方程: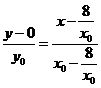
化简得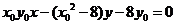
又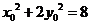 ,
,
所以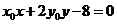 带入
带入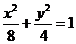
求得最后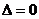
所以直线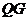 与椭圆只有一个公共点.
与椭圆只有一个公共点.
【考点定位】考查椭圆的标准方程及其几何性质,直线和椭圆的位置关系,并考查数形结合思想,逻辑推理能力及运算能力.












