评论
打印
二．填空题
11. 设函数发f（x）=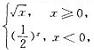
，则f（f（-4））= 4
解析：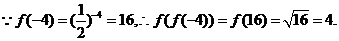
答案：4
点评：本题主要考察分段函数求值，主要是要正确把握函数的概念.
12.
观察下列不等式
，
……
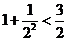
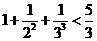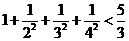
照此规律，第五个不等式为 1+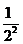
+
+
+
+
<
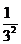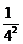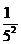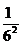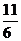
解析：观察这几个不等式可以发现左边分母从1、2、3、4、5的平方依次增加1后的平方，分子全是1，右边分母是左边最后一项的分母的底数，分子式左边后两分母底数的和，于是有：
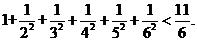
答案：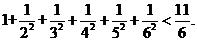
点评：该题主要考察归纳推理，从给出的几个不等式的特征猜测出一般的规律正是归纳推理的本质所在.
13. 在三角形ABC中，角A,B,C所对应的长分别为a，b，c，若a=2 ，B=
，c=2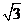
，则b= 2
解析：因为已知两边及其夹角，所以直接用余弦定理得b=2.
答案：2
点评：此题主要考察用余弦定理解三角形，掌握定理是关键.
14.右图是抛物线形拱桥，当水面在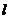
时，拱顶离水面2米，水面宽4米，水位下降1米后，水面宽 
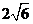米。
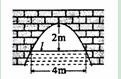
解析：先以拱顶为原点，建立直角坐标系，设水面和拱桥交点A（2，-2）则抛物线方程为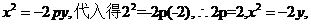
当水面下降1米时，水面和拱桥的交点记作B（a,-3)则代入抛物线方程得：a=
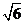,因此水面宽2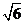米.
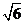答案：2米
点评：本题主要考察抛物线的标准方程及其应用，紧扣课本.
15.A （不等式选做题）若存在实数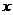
使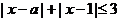
成立，则实数
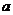的取值范围是 解析：由题意知左边的最小值小于或等于3即可，根据不等式的性质得
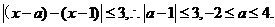
答案：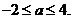
点评：本题主要考察绝对值不等式的性质及其运用.
15 B （几何证明选做题）如图，在圆O中，直径AB与弦CD垂直，垂足为E，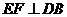
，垂足为F，若
，
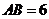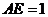，则
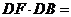5
解析：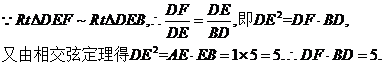
答案：5
点评：该题主要考察直线和圆的位置关系的证明与计算.
15 C （坐标系与参数方程）直线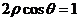
与圆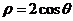
相交的弦长为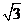
解析：化极坐标为直角坐标得直线
答案：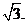
点评：本题主要考察极坐标系与极坐标方程，先化为普通方程后求解.
