第Ⅱ卷(共90分)
二、填空题(每题4分,满分16分,将答案填在答题纸上)
(13) 的展开式中常数项是______________.
的展开式中常数项是______________.

(14)如图,正方体的棱长为1,C、D分别是两条棱的中点,A、B、M是顶点,那么点M到截面 的距离是_____________.
的距离是_____________.


(15)用1、2、3、4、5、6、7、8组成没有重复数字的八位数,要求1与2相邻,3与4相邻,5与6相邻,而7与8不相邻,这样的八位数共有___________个.(用数字作答)

(16) 是正实数,设
是正实数,设 ,若对每个实数a ,
,若对每个实数a ,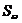 ∩
∩ 的元素不超过2个,且有a使
的元素不超过2个,且有a使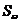 ∩
∩ 含有2个元素,则
含有2个元素,则 的取值范围是___________.
的取值范围是___________.

【点拨】通过数轴得出 ∩
∩ 元素个数与两点间距离的关系再求解.
元素个数与两点间距离的关系再求解.
三、解答题 (本大题共6小题,共74分.解答应写出文字说明、证明过程或演算步骤.)
(17)(本小题共12分)。
已知三棱锥P-ABC中,E、F分别是AC、AB的中点,△ABC,△PEF都是正三角形,PF⊥AB.

(Ⅰ)证明PC⊥平面PAB;
(Ⅱ)求二面角P-AB-C的平面角的余弦值;
(Ⅲ)若点P、A、B、C在一个表面积为12π的球面上,求△ABC的边长.


( 18 )(本小题共12分)
如图,在直径为1的圆 中,作一关于圆心对称、邻边互相垂直的十字形,其中
中,作一关于圆心对称、邻边互相垂直的十字形,其中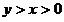 .
.
(Ⅰ) 将十字形的面积表示为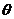 的函数;
的函数;
(Ⅱ) 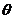 为何值时,十字形的面积最大?最大面积是多少?
为何值时,十字形的面积最大?最大面积是多少?


可解得 ……10分
……10分
所以,当 时,S最大,S的最大值为
时,S最大,S的最大值为 ……12分
……12分
( 19 )(本小题共12分)
已知函数 .设数列
.设数列 满足
满足 ,
, ,数列
,数列 满足
满足
 ,
, …
… ,
,
(Ⅰ)用数学归纳法证明 ;(Ⅱ)证明
;(Ⅱ)证明  .
.














