(18)(本小题满分12分)
平面图形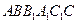 如图4所示,其中
如图4所示,其中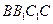 是矩形,
是矩形,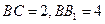 ,
,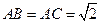 ,
,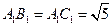 。现将该平面图形分别沿
。现将该平面图形分别沿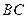 和
和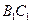 折叠,使
折叠,使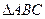 与
与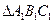 所在平面都与平面
所在平面都与平面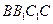 垂直,再分别连接
垂直,再分别连接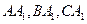 ,得到如图2所示的空间图形,对此空间图形解答下列问题。
,得到如图2所示的空间图形,对此空间图形解答下列问题。
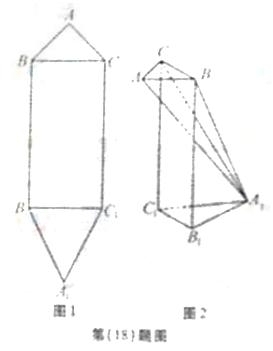 。
。
(Ⅰ)证明: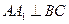 ;
;
(Ⅱ)求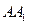 的长;
的长;
(Ⅲ)求二面角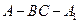 的余弦值。
的余弦值。
【解析】(I)取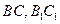 的中点为点
的中点为点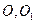 ,连接
,连接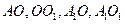
则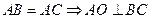 ,面
,面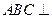 面
面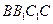
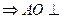 面
面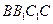
同理: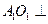 面
面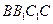 得:
得: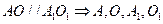 共面
共面
又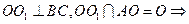
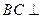 面
面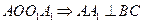
(Ⅱ)延长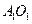 到
到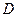 ,使
,使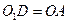 得:
得: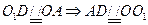
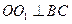 ,面
,面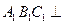 面
面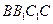
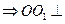 面
面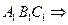
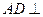 面
面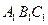
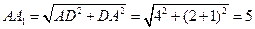
(Ⅲ)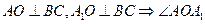 是二面角
是二面角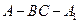 的平面角
的平面角
在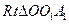 中,
中,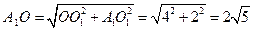
在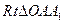 中,
中,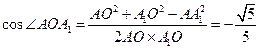
得:二面角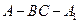 的余弦值为
的余弦值为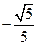 。
。
(19)(本小题满分 13分)K]
13分)K]
设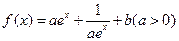
(I)求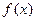 在
在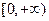 上的最小值;
上的最小值;
(II)设曲线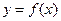 在点
在点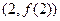 的切线方程为
的切线方程为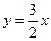 ;求
;求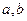 的值。
的值。
【解析】(I)设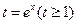 ;则
;则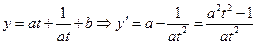
①当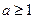 时,
时,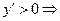
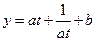 在
在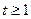 上是增函数
上是增函数
得:当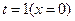 时,
时,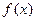 的最小值为
的最小值为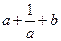
②当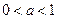 时,
时,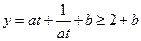
当且仅当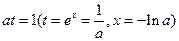 时,
时,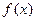 的最小值为
的最小值为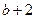
(II)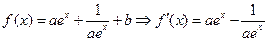
由题意得: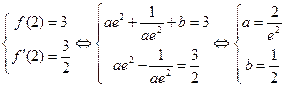
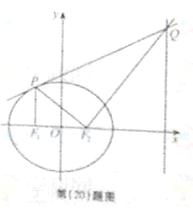
(20)(本小题满分13分)
如图,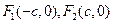 分别是椭圆
分别是椭圆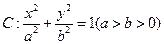 的左,右焦点,过点
的左,右焦点,过点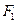 作
作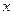 轴的垂线交椭圆的上半部分于
轴的垂线交椭圆的上半部分于 点
点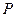 ,过点
,过点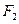 作直线
作直线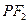 的垂线交直线
的垂线交直线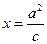 于点
于点 ;
;
(I)若点 的坐标为
的坐标为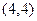 ;求椭圆
;求椭圆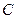 的方程;
的方程;
(II)证明:直线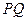 与椭圆
与椭圆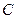 只有一个交点。
只有一个交点。
【解析】(I)点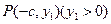 代入
代入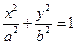 得:
得: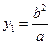
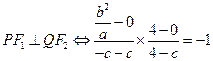 ①
①
又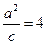 ②
② 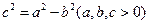 ③
③
由①②③得: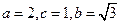 既椭圆
既椭圆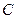 的方程为
的方程为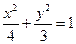
(II)设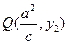 ;则
;则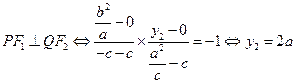
得: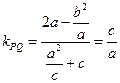
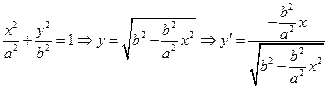
过点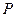 与椭圆
与椭圆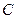 相切的直线斜率
相切的直线斜率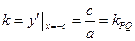
得:直线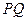 与椭圆
与椭圆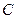 只有一个交点。
只有一个交点。
(21)(本小题满分13分)
数列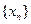 满足:
满足: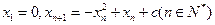
(I)证明:数列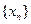 是单调递减数列的充分必要条件是
是单调递减数列的充分必要条件是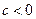
(II)求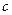 的取值范围,使数列
的取值范围,使数列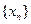 是单调递增数列。
是单调递增数列。
【解析】(I)必要条件
当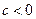 时,
时,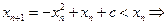 数列
数列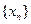 是单调递减数列
是单调递减数列
充分条件
数列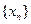 是单调递减数列
是单调递减数列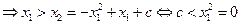
得:数列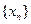 是单调递减数列的充分必要条件是
是单调递减数列的充分必要条件是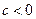
(II)由(I)得: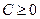
①当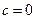 时,
时,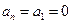 ,不合题意
,不合题意
②当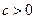 时,
时,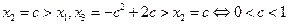

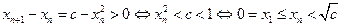
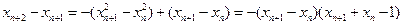
当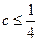 时,
时,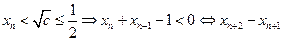 与
与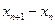 同号,
同号,
由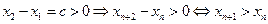
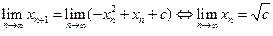
当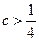 时,存在
时,存在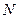 ,使
,使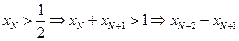 与
与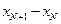 异号
异号
与数列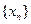 是单调递减数列矛盾
是单调递减数列矛盾
得:当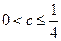 时,数列
时,数列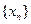 是单调递增数列
是单调递增数列












