第Ⅰ卷(选择题 共50分)
一.选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中.只有一项是符合题目要求的.
(1)若A=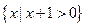 ,B=
,B=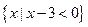 ,则
,则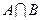 =
=
(A)(-1,+∞)(B)(-∞,3)(C)(-1,3) (D)(1,3)
(D)(1,3)
1.【答案】C
【命题意图】此题主要考查集合和不等式的基础知识,基本的运算能力
【解析】:对于A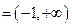 ,
,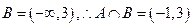 ,宜选C
,宜选C
(2)已知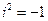 ,则i(
,则i(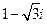 )=
)=
(A)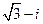 (B)
(B)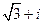 (C)
(C)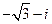 (D)
(D)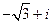
2.【答案】B
【命题意图】此题主要考查复数的基础知识和考生对于复数化简的能力
【解析】: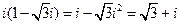
(3)设向量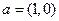 ,
,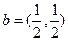 ,则下列结论中正确的是
,则下列结论中正确的是
(A)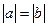 (B)
(B)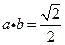
(C)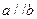 (D)
(D)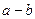 与
与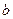 垂直
垂直
3.【答案】D
【命题意图】此题主要考查向量的坐标运算知识和运用向量判断位置关系的能力
【解析】:因为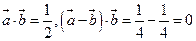 ,因此
,因此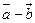 与
与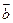 垂直
垂直
(4)过点(1,0)且与直线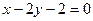 平行的直线方程是
平行的直线方程是
(A)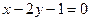 (B)
(B)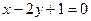
(C)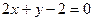 (D)
(D)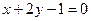

(5)设数列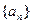 的前n项和
的前n项和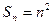 ,则
,则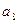 的值为
的值为
(A)15 (B)16 (C)49 (D)64
5.【答案】A
【命题意图】此题主要考查数列的基础知识,数列中的某一项的求解方法
【解析】:对于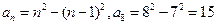
(6)设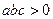 ,二次函数
,二次函数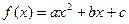 的图象可能是
的图象可能是
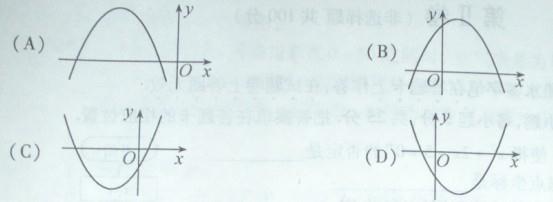
6.【答案】D
【命题意图】此题主要考查函数的图象和性质和考查学生看图识图的能力
【解析】:对于A中的图可得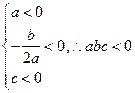 ,对于B中的图可得
,对于B中的图可得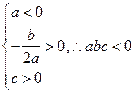 ,对于C中的图可得
,对于C中的图可得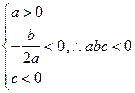 ,对于D中的图可得
,对于D中的图可得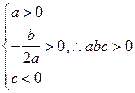
(7)设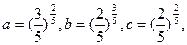 则a,b,c的大小关系
则a,b,c的大小关系
是
(A)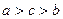 (B)
(B)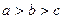
(C)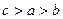 (D)
(D)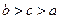
7.【答案】A
【命题意图】此题主要考查指数函数和幂函数的单调性和运用函数单调性判断数大小的能力
【解析】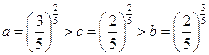
(8)设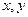 满足约束条件
满足约束条件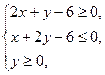 则目标函数
则目标函数
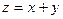 的最大值是
的最大值是
(A)3 (B)4 (C)6 (D)8
8.【答案】C
【命题意图】此题主要考查线性规则中的线性区域和目标函数的求解方法
【解析】对于目标函数过线性区域上点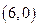 时
时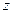 值最大,
值最大,
(9)一个几何体的三视图如图,该几何体的表面积是
(A)372 (C)292
(B)360 (D)280

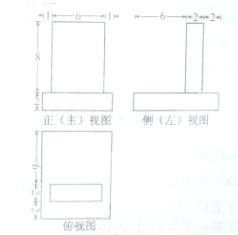
9.【答案】B
【命题意图】此题主要考查此题主要考查几何体的三视图的基础知识,考查了考生运用三视图还原直观图的能力
(10)甲从正方形四个顶点中任意选择两个顶点连成直线,一页从该正方形四个顶点中任意选择连个顶点连成直线,则所得的两条直线相互垂直的概率是
(A)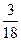 (A)
(A)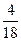 (A)
(A)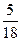 (A)
(A)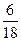
10.【答案】C
【命题意图】此题主要考查概率的基础知识和运用例举法计数的能力
【解析】基本事件有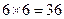 种,而符合两直线互垂直的有10种情况,即符合条件的概率为
种,而符合两直线互垂直的有10种情况,即符合条件的概率为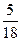
第Ⅱ卷(非选择题共100分)
二.填空题:本大题共5小题,每小题5分,共25分.把答案填在答题卡的相应位置·
(11)命题“存在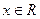 ,使得
,使得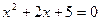 ”的否定是。
”的否定是。
11.
【命题意图】此题主要考查命题的否定基础知识及逻辑联系词的基本应用
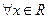 ,使得
,使得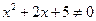
【解析】对于“存在”的反面是“任意”,“等于”的反面是“不等于”因此原命题的否定是“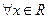 ,使得
,使得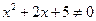 ”
”
(12)抛物线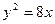 的焦点坐标是 。
的焦点坐标是 。
12.【答案】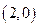
【命题意图】此题主要考查抛物线的定义和基本性质
【解析】因为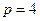 ,因此焦点为
,因此焦点为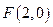
(13)如图所示,程序框图(算法流程图)的输出值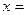 。
。
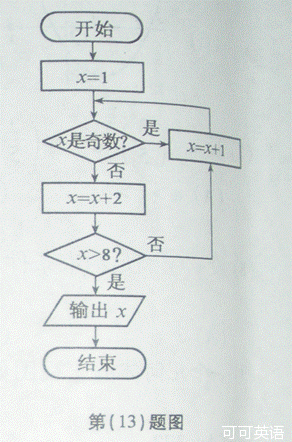
13.【答案】12
【命题意图】此题主要考查程序运算的基本方法和逻辑运算
【解析】依程序对于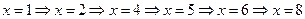
(14)某地有居民100000户,其中普通家庭99 000户,高收入家庭1 000户.从普通家庭中以简单随机抽样方式抽取990户,从高收入家庭中以简单随机抽样方式抽取l00户进行调查,发现共有120户家庭拥有3套或3套以上住房,其中普通家庭50户,高收人家庭70户.依据这些数据并结合所掌握的统计知识,你认为该地拥有3套或3套以上住房的家庭所占比例的合理估计是 .

(15)若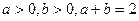
 ,则下列不等式
,则下列不等式 对一切满足条件的
对一切满足条件的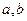 恒成立的是(写出所有正确命题的编号)。
恒成立的是(写出所有正确命题的编号)。
①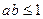 ②
②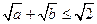 ;③
;③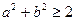 ;
;
④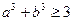 ; ⑤
; ⑤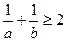
15.【答案】①③⑤
【命题意图】此题主要考查基本不等式的基础知识和考生运用基本 不等式论证数量关系的能力
不等式论证数量关系的能力
【解析】对于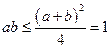 ,对于
,对于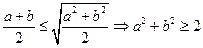 ,
,
对于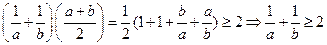 ,因此①③⑤正确,而其余的可取特殊值
,因此①③⑤正确,而其余的可取特殊值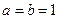 时就不成立
时就不成立
三、解答题:本大题共6小题.共75分.解答应写出文字说明、证明过程或演算步骤.解答写在答题卡上的指定区域内。
(16)△ABC的面积是30,内角A,B,C,所对边长分别为a,b,c,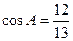 .
.
(Ⅰ)求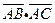
(Ⅱ)若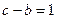 ,求
,求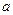 的值。
的值。
16.
【命题意图】此题主要考查三角函数、三角形与向量的基础知识,考查考生运用方程思想、转化思想的能力
【解析】
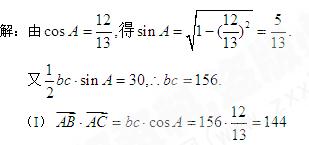
(II)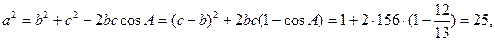
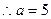
【点评】对于三角形问题的考查一般可用正弦定理、余弦定理进行化解,而涉及到向量问题则可考虑向量有坐标运算和线性运算两个方向;对于边长的求解一般就用余弦定理,当然运用余弦定理一定要注意其运用条件
(17)(本小题满分12分)
椭圆E经过点A(2,3),对称轴为坐标轴,焦点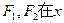 轴上,离心率
轴上,离心率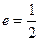 。
。
(Ⅰ)求椭圆E的方程;
(Ⅱ)求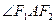 的角平分线所在直线的方程。
的角平分线所在直线的方程。
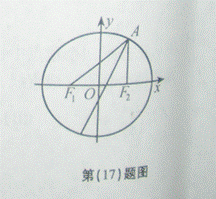
17.
【命题意图】此题主要考查椭圆的定义和直线方程的求解方法,考查考生运用点到直线距离求解参数的能力
【解析】
解:(I)设椭圆E的方程为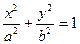
3
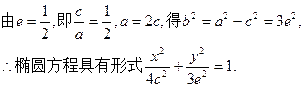

【点评】椭圆基础问题的化解一般就是根据椭圆的定义进行化解,对于涉及到直线方程的求解则要结合方程思想通过点到直线的距离进行处理;化解解析几何问题关键是按圆锥曲线的定义、从几何性质入手进行转化处理,以不变应万变












